Научиться рассчитывать по формуле оптимальный размер заказа [c.223]
Как мы видим, формула оптимального размера заказа дает такой же результат, что и графический метод. Полученный результат говорит о том, что для минимизации затрат размер заказа должен составить 100 единиц, при этом периодичность размещения заказов должна быть равна 600/100 = 6 раз в год. [c.233]
Следовательно, чтобы минимизировать затраты, рекомендуется размер заказа в 693 единицы. В предыдущем примере, когда мы использовали графический метод, результат составил приблизительно 700 единиц. Формула оптимального размера заказа подтверждает приемлемость этого значения. Однако, ясно, что вряд ли размер заказа составит 693 единицы. На практике, если округлить это значение до 700, то получится более реальная цифра. Как мы уже говорили, возможно, будет выбран размер заказа в 800 единиц, так как в этом случае периодичность размещения заказов будет более реальной и целесообразной, то есть составит две недели. [c.233]
Точка заказа и цикл заказа приведены на рис. 7.5. Необходимо отметить, что на этом графике уровень запасов следует той же самой модели, что и в одном из предыдущих примеров. Таким образом, мы можем применить формулу оптимального размера заказа, которой мы пользовались в предыдущих разделах. Знание цикла заказа может повлиять на формулирование политики по размещению заказов. Так, в предыдущих примерах конкретизировалась периодичность размещения заказов, или время между заказами, например размещать заказ на 30 единиц товара каждые 2 месяца. Как вариант, если мы знаем цикл заказа, то можно точно определить точку заказа, например размещать заказ на 30 единиц товара тогда, когда уровень запасов составит 12 единиц товара. В этой простой модели, где спрос постоянен, фактические результаты аналогичны. Однако в последующих, более сложных моделях определение политики размещения заказов компании может оказаться значимым при оценке эффективности мероприятий по управлению запасами. [c.237]
Итак, определяем оптимальный размер заказа, как мы это делали раньше, — исходя из значений спроса, расходов на подготовку заказа, расходов на хранение и цены приобретения единицы товара. В этом примере следует взять среднее значение спроса. Кроме того, стандартный период равен четырем дням. То есть расходы на хранение за год должны быть преобразованы, и только потом полученное значение можно подставить в формулу оптимального размера заказа. [c.246]
Применение формулы оптимального размера заказа [c.294]
Используя формулу, мы сделали ряд предположений для упрощения задачи. Прежде всего было принято, что нормы потребления в период между заказами будут постоянными, т. е. что средний уровень запаса составит половину годового потребления. Мы также допустили, что с точки зрения использования складских площадей каких-либо ограничений нет. Выведенный по формуле оптимальный размер заказа оказывается действительным лишь в том случае, если в нормах потребления в течение года, в издержках по содержанию запаса и оформлению заказа не произойдет каких-либо изменений. Изменение стоимости единицы товара,, очевидно, повлияет на общую сумму годового потребления в долларах, что соответственным образом изменит количественный оптимум заказа. Единственным способом компенсировать влияние этих факторов будет новый расчет и подстановка в формулу новых данных. [c.374]
В условиях определенности для нахождения средних оптимальных трансакционных остатков может применяться формула оптимального размера заказа, используемая в управлении товарно-материальными ценностями. В этой модели накладные расходы хранения наличности, т. е. процент по рыночным ценным бумагам, от которого отказывается фирма, сопоставляются с постоянными расходами по переводу ценных бумаг в наличность и обратно. [c.371]
В специальной литературе вывод Р. Уилсоном формулы оптимального размера заказа датируется в пределах от 1916 [c.51]
Оптимальный размер заказа можно рассчитать с помощью таблицы совокупной стоимости заказов различной величины, графически или формулы. [c.88]
Страховой запас, расчет оптимального размера. Оптимальный размер заказа и момент его размещения у поставщика или на производстве зависят от величины страхового запаса. Рассмотренные выше формулы расчетов действенны при определенных условиях точности прогнозов, своевременного пересмотра сроков поставок, недопущении дублирования заказов, хранении страховых запасов у по-ставщика. [c.93]
К). Дайте определение оптимального размера заказа, приведите формулы расчета. [c.102]
Значение оптимального размера заказа, которое мы в предыдущих примерах определяли с помощью графического метода, можно рассчитать и по математической формуле. Эта формула основывается на нахождении минимального значения на графике исходя из общих затрат. Мы приведем эту формулу в данном разделе, однако в задачу настоящего пособия не входит описание того, как она получена. Мы будем пользоваться следующими обозначениями [c.232]
Имея эти переменные, рассчитываем значение оптимального размера заказа по следующей формуле [c.232]
Мы описали некоторые важные модели управления запасами, в частности модель оптимального размера заказа, основанную на учете постоянного спроса (D), фиксированной цены за единицу товара (Р), расходов на хранение (//), которые иногда дают как процент (/) от стоимости запасов, а также расходов на подготовку заказа (Q. С помощью этой модели рассчитывается оптимальный размер заказа, минимизирующий расходы на подготовку заказа и хранение запасов. При этом применяется следующая формула [c.256]
Модель размера производственного заказа исходит из тех же посылок, что и модель оптимального размера заказа, но дополнительно к этому пользователь является также и производителем с известной нормой выпуска (К). В этом случае оптимальный размер производственного заказа рассчитывается по следующей формуле [c.256]
Оптимальный размер заказа. Исходя из формулы (10.2) мы можем получить оптимальный размер заказа [c.293]
Из данных таблицы 37 легко понять, как выводится формула расчета оптимального размера заказа (EOQ). Последовательно раскладывая строку (9) по остальным строкам таблицы 37, получают следующие результаты [c.261]
Значение (OQ) в точке, где совокупные издержки минимальны, есть не что иное, как оптимальный размер заказа (EOQ). Таким образом от обратного можно вывести исходную формулу [c.262]
Подставляя цифровые значения из таблицы 37 в формулу модели (EOQ), получим величину оптимального размера заказа (одной партии закупок материала), равную [c.262]
Оптимальный размер заказа по критерию минимизации совокупных затрат на хранение запаса и повторение заказа рассчитывается по формуле (она называется формулой Вильсона) [c.238]
Оптимальный размер заказа, шт. См. формулы (7.1) и (7.2) [c.239]
Расчет оптимального размера заказа для всех комплектующих по формуле (7.1). [c.254]
Напишите формулу определения оптимального размера заказа. [c.256]
Рассчитать оптимальный размер заказа для всех комплектующих изделий по формуле [c.15]
Решение. По формуле (2) рассчитаем рекомендуемый интервал времени между заказами (табл. 5.5). Пусть оптимальный размер заказа равен 75 шт. (см. задачу 16) [c.165]
Оптимальный размер заказа, шт. По формуле (I) [c.259]
Оптимальный размер заказа рассчитывается по формуле Вильсона [c.259]
Низкое качество данных говорит о том, что более сложные математические расчеты, а таких немало, не стоят рассмотрения, поскольку их преимущество над описанным выше простейшим подходом измеряется с использованием столь же некачественных исходных данных. На рис. 8.4 показано, как сказываются погрешности в первичной информации на результате формулы расчета оптимального размера заказа. Если любая комбинация величин неверна в указанное по горизонтали число раз, то по вертикали получим изменение затрат на хранение и приобретение. Например, если истинные затраты на приобретение в два раз больше (или вполовину меньше) используемого в расчетах значения, то общие затраты вырастут на 6%. [c.170]
| Рис. 8.4. Чувствительность формулы расчета оптимального размера заказа | 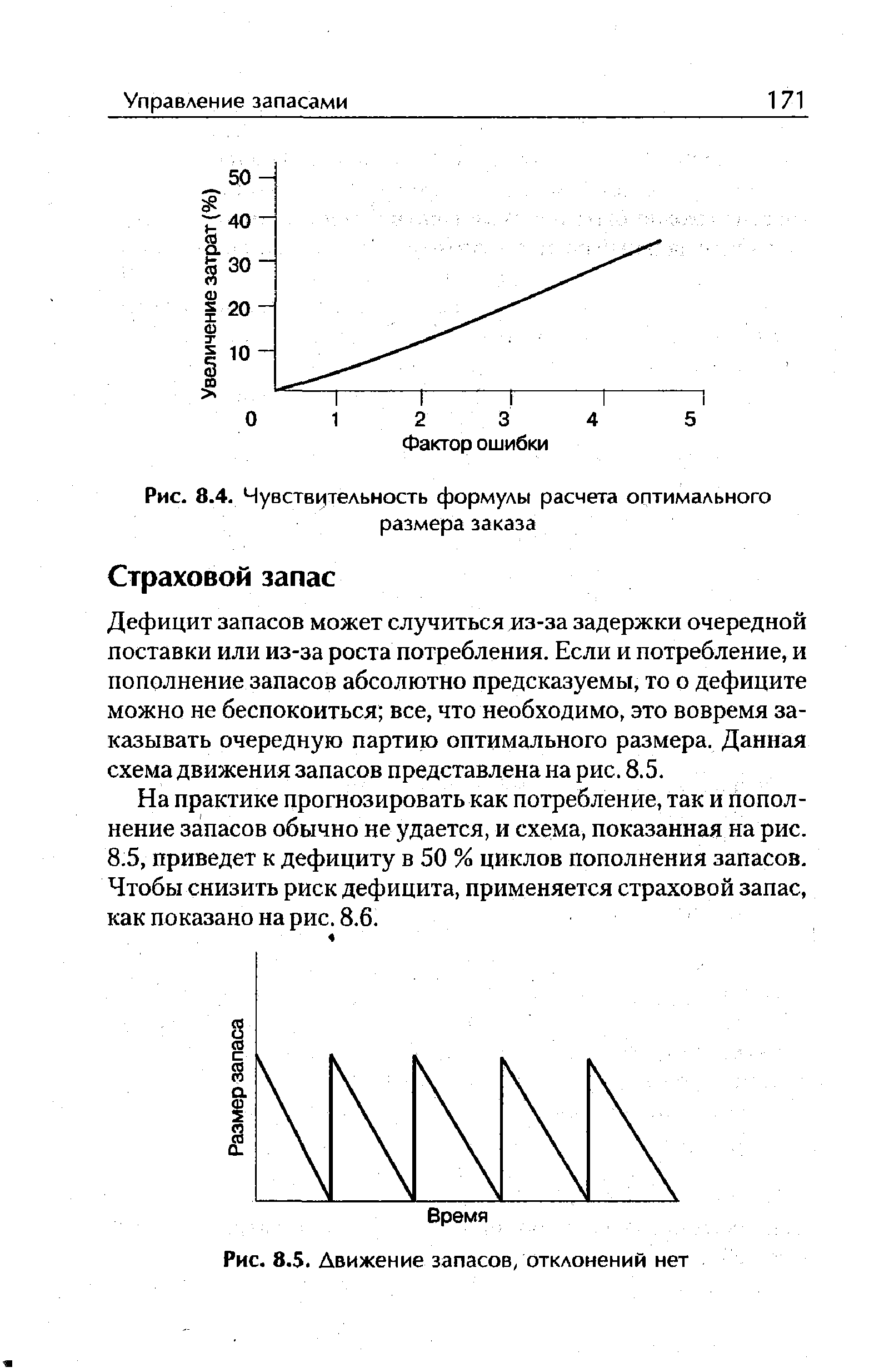 |
Если цена единицы материала не зависит от размера заказа (т. е. скидок нет), включение в формулу стоимости самих материалов не повлияет на оптимальный размер заказа, а кривая суммарных издержек сместится вверх на постоянную величину. [c.262]
Формулы для оптимального размера заказа и оптимальной величины дефицита [c.182]
Формально это видно из формулы для оптимального размера заказа в модели с планируемым дефицитом (вкладка 6). По сравнению с формулой для EOQ эта формула содержит множитель (Н + СХ)1СХ, который не может быть меньше единицы, следовательно, оптимальный размер заказа в модели с планируемым дефицитом выше, чем EOQ. [c.272]
Отношение величины потребности к оптимальному размеру заказа равно количеству заказов в заданный период. Число рабочих дней в заданном периоде, отнесенное к количеству заказов, равно интервалу между заказами, соответствующему оптимальному режиму работы системы. Таким образом, интервал времени между заказами можно рассчитать по формуле [c.135]
Срок годности при хранении. Это важная характеристика, учитываемая при определении уровня запасов. Так, многие лекарства, складированные в аптеках Литлвудз , имеют короткий срок годности хранения. То есть общий уровень запасов в любой момент времени не должен превышать количества, необходимого в течение срока годности товара. Рассмотрим хранение хлеба в крупном магазине. Хлеб необходимо употребить в течение 5 дней, а текущий спрос на него составляет 1000 булок в день. Следовательно, максимальный уровень запасов данного товара должен быть не более 5000 булок. На практике же уровень запасов товара может быть значительно ниже этой цифры. Однако если взять формулу оптимального размера заказа, то можно получить, что по отношению собственно к затратам оптимальное количество равно 6000 булок. Для опреде- [c.254]
В условиях определенности для нахождения средних оптимальных трансакционных остатков может применяться формула оптимального размера заказа (e onomi -order-quantity — EOQ), используемая в управлении товарно-материальными ценностями. Эта модель дает хорошее концептуальное обоснование проблемы [c.264]
Г -> min. Дифференцирование по бдает формулу расчета оптимального размера заказа (формулу Вильсона) [c.158]
Во-первых, это видно из приведенного численного примера "Продажа машин со стоянки". Для читателей, имеющих вкус к точным математическим результатам, можно рекомендовать подставить формулы для оптимального размера заказа Qopl и оптимального размера дефицита Л , в выражение для T Q, X). После простых преобразований для Т получится формула [c.273]
Смотреть страницы где упоминается термин Формула оптимального размера заказа
: [c.99] [c.726] [c.234] [c.234] [c.295] [c.216] [c.158]Смотреть главы в:
Количественные методы анализа хозяйственной деятельности -> Формула оптимального размера заказа
