Центрированные скользящие средние [c.192]
В этом примере мы рассмотрим ситуацию, когда при вычислении скользящих средних берется четное число значений. В этом случае для определения тренда временного ряда мы будем пользоваться значениями центрированных скользящих средних. В таблице ниже представлены данные по двухмесячному объему производства среднего предприятия обрабатывающей отрасли промышленности, расположенного в Дублине. (Цифры общего объема производства за каждые два месяца даны в тоннах.) [c.203]
Период - - Объем производства - Центрированные скользящие средние [c.203]
Так получается, что эти скользящие средние не соответствуют точно какому-либо значению объема производства, и поэтому в таблице они помещаются по центру между строк. Итак, мы рассчитали центрированные скользящие средние и поместили их в таблицу — типа той, что приведена на стр. 204. Затем получаем значения отклонений путем вычитания значений центрированных [c.203]
Значения объема производства и центрированные скользящие средние представлены на графике (рис. 6.11). Из графика видно, что центрированные скользящие средние используются при получении оценочных показателей тренда на следующий год (1999). Согласно графику оценочные показатели по тренду в каждом из периодов 1999 г. составляют [c.204]
Сглаживание графика с помощью скользящих средних, центрированных скользящих средних или экспоненциального сглаживания. [c.221]
Тренд, центрированные скользящие средние 192 [c.422]
Центрированные скользящие средние 192 Цикл заказа 237, 255 Циклические колебания 210 [c.422]
С помощью скользящих можно определить длину периода цикла движения рынка, о чем будет рассказано в разделе о Теории Циклов. Важно, что при этом используют центрированные скользящие средние, т.е. смещенные назад на половину порядка. [c.103]
Год Квартал Период, f Количество товара, ед. Скользящие средние Центрированные скользящие средние Оценка сезонной компоненты [c.441]
Номер кварт. Объем продаж А Итого за 4 квартала Скользящая средняя за 4 квартала (гр.З 4) Центрированная скользящая средняя Т Оценка сезонной компоненты A-T=S+E [c.117]
Центрированные скользящие средние (гр.5 табл. 7.1.3) получены как средняя величина для каждой пары Значений. [c.118]
Для сглаживания неинтегрированного лунного ряда ценовых изменений использовалось центрированное скользящее среднее. При этом не возникало запаздывания, поскольку центрированное скользящее среднее для данного дня учитывает одинаковое количество предшествующих и последующих точек данных. Такое сглаживание применимо, поскольку оценка лунных циклов основывается на данных минимум двухмесячной давности. Для сглаженного ряда изменений цены строился ряд средних абсолютных отклонений и вычислялось простое скользящее среднее с периодом [c.219]
При четном интервале сглаживания используется специальная процедура центрирования, состоящая в том, что рассчитывается средняя из двух смежных скользящих средних для того, чтобы соотнести полученный уровень с определенной датой. [c.372]
Для определения сглаженных уровней производится центрирование. При применении метода скользящей средней к ряду динамики месячных уровней рассчитывается 12-членная скользящая средняя. [c.174]
Для сглаживания влияния случайных факторов проводится центрирование подвижных средних, в результате строится динамический рад скользящих средних. [c.179]
Год, квартал Исходные уровни Скользящие средние Сглаженные уровни с центрированием [c.183]
Решение. Производим расчет 5-летних средних и заполняем табл. 3.14. Скользящая средняя дает более или менее плавное изменение уровней. Проводим центрирование, заключающееся в нахождении средней из средних для отнесения полученного уровня к определённой дате. [c.103]
Если т — четное, то задача несколько усложняется, так как средние точки будут расположены между точками, по которым выполнялся расчет. Например, если т = 4, то первое скользящее среднее окажется между второй и третьей точками, второе скользящее среднее — между третьей и четвертой и т. д. В этом случае требуется процедура центрирования полученных значений. Центрированное значение находится как среднее от двух скользящих средних, находящихся между точками. Например, центрированное значение для третьей точки — это среднее от скользящих средних, расположенных между второй и третьей, третьей и четвертой точками. [c.182]
Третий этап — определение сезонной компоненты. Дальнейшие расчеты будут зависеть от выбора вида модели прогноза. Для аддитивной модели (7.4) рассчитывается оценка сезонной компоненты как разность между фактическим значением и значением, определенным по трен-довой модели (первый вариант оценки тренда). Или фактическим значением и скользящей средней (при нечетном т), или фактическим значением и центрированной средней (при четном т), если использовался второй вариант оценки тренда. [c.182]
Для мультипликативной модели (7.5) при первом варианте оценки тренда находится отношение фактических значений показателя к расчетным, определенным по трендовой модели. Во втором варианте оценки тренда находится отношение фактических значений показателя к скользящей средней (при нечетном т) или к центрированной средней (при четном /и). Такое отношение называется индексом (коэффициентом) сезонности. [c.182]
Рассмотрим другой пример, в котором данные представлены поквартально. В табл. П-14 представлено определение оценок сезонной компоненты в аддитивной и мультипликативной моделях. Поскольку сезонные колебания имеют периодичность, равную 4 кварталам, в данном примере помимо определения скользящих средних требуется рассчитать центрированные значения средних. [c.439]
Центрирование среднего скользящего [c.230]
Наиболее статистически верным способом построения среднего скользящего является центрирование (см. рис. 9.8 а и б). Центрированием называют такой вид построения, когда среднее скользящее устанавливают в центр временного периода, который оно охватывает. Например, десятидневное среднее скользящее строят с пятидневным запаздыванием, двадцатидневное - с десятидневным. Однако центрирование как способ построения среднего скользящего имеет один крупный недостаток - сигнал, знаменующий смену тенденции, значительно запаздывает. Поэтому среднее скользящее обычно откладывается в конце периода, а не в середине. Метод центрирования используется почти исключительно аналитиками, занимающимися циклическим анализом, так как центрирование помогает выделять рыночные циклы. В главе 14 мы остановимся несколько подробнее на том, как это делается. [c.230]
Pu . 14. 20a Пример сорокадневного центрированного среднего скользящего, построенное на графике цен контракта на индекс S P. [c.391]
Процедура снятия направленности сравнительно проста (см. примеры на рис. 14. 20а-г). Ее можно выполнить вручную, но проще и удобнее с помощью компьютера. Прежде всего выбирают период для расчета среднего скользящего. Он определяется длительностью цикла, который необходимо выделить. В качестве примера мы возьмем сорокадневное среднее скользящее. Следующим шагом является центрирование среднего скользящего. Речь идет о том, что среднее значение откладывается на двадцать первый день периода расчета (середина цикла), а не на последний день, как это делают обычно. Затем среднее скользящее откладывают в виде нулевой линии внизу графика, а показатели цен наносят выше и ниже этой линии. В результате циклы, продолжительность которых составляет меньше сорока дней, становятся гораздо более выраженными, следовательно, их легче установить. Далее процедуру можно продолжить, выделяя все более и более короткие периоды - пока не будут установлены все доминирующие циклы. Программа по снятию направленности входит в пакет "Компутрэк". [c.393]
При дальнейшем анализе этих данных нам придется рассматривать скользящие средние и соответствующие фактические значения. Для этого вычисляются центрированные скользящие средние. Они рассчитываются путем нахождения среднего каждой пары значений скользящих средних. Это есть — двухточечная скользящая средняя скользящих средних. Полученные значения приведены в таблице ниже. [c.192]
А теперь центрированные скользящие средние можно использовать для прогнозирования тренда. Значения, если их нанести на график, совпадут по горизонтальной оси с исходными данными. Рассчитайте самостоятельно четырехточечные скользящие средние, а затем центрированные скользящие средние для всех данных таблицы объема продаж, приведенной в предыдущем разделе. [c.192]
Год Период Объем производства Шеститочечные скользящие средние Центрированные скользящие средние Отклонения [c.204]
Традиционно расчетную величину скользящего среднего принято соотносить с ценой последнего торгового дня. Подобная практика, считающаяся у аналитиков чем-то священным, всегда вызывала у меня множество вопросов. Я много экспериментировал с центрированием скользящего среднего и добился некоторого улучшения результатов. Вместо того чтобы выводить скользящее среднее в той же временной точке, где выводится последняя цена, как поступает болыиин-ство трейдеров, я проработал методику, при которой спроецированное среднее значение соотносится с ценой текущего дня. В некотором смысле можно сказать, что [c.93]
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 5.8). Используем эти оценки для расчета значений сезонной компоненты S (табл. 5.9). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Sf. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. [c.242]
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 5.12). Используем эти оценки для расчета значений сезонной компоненты S (табл. 5.13). Для этого найдем средние за каждый квартал оценки сезонной компоненты 51,-. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла (год) равно 4 (четыре квартала). [c.247]
Посередине между двумя уже упомянутыми методиками лежит инструмент, основанный на особого рода проецировании цены. Его называют снятие направленности (detrending). Первый шаг снятия направленности — построение определенной скользящей средней и ее центрирование. Затем график цен проецируется относительно скользящей средней, при этом значения берутся либо как расстояние, либо как проценты между скользящей и действительным значением. После этого наглядными становятся максимумы и минимумы графика, позволяющие определить его периодичность (рис. 8.5). В зависимости от того, какой цикл требуется выявить — более или менее долгосрочный, берут скользящие средние соответствующего порядка (например, 40 дней). А чтобы выявить более мелкие доминантные составляющие, в соответствии с принципом гармоничности последовательно выбирают периоды в 2 раза короче (20, 10, 5 дней). Возможно использование порядков скользящих средних, близких к членам Последовательности Фибоначчи. [c.131]
На рис. 7.5 представлен график цены сырой нефти на NYMEX за один год. Представленные огибающие являются 2.5-процентной полосой торговли, центрированной относительно 14-дневного скользящего среднего. Выбранное скользящее среднее хорошо представляло краткосрочные тенденции цены на сырую нефть в том году, а значение 2.5 процента является широко используемым на рынках параметром. Выбирая параметры полосы так, чтобы она охватывала нормальную волатильность, аналитик может определить, имеет ли место ситуация перекупленно-сти/перепроданности при выходе цены за пределы канала. Анализ можно сделать более чувствительным путем уменьшения ширины полосы и менее чувствительным путем увеличения его ширины. [c.74]
| Рис. 9.86 Гак- выглядит то же двадцатиоднодневное среднее скользящее после центрирования Можно заметить, что прогностические способности кривой такого индикатора, в основном, довольно слабы. Метод центрирования наиболее эффективен при выявлении рыночных циклов. | 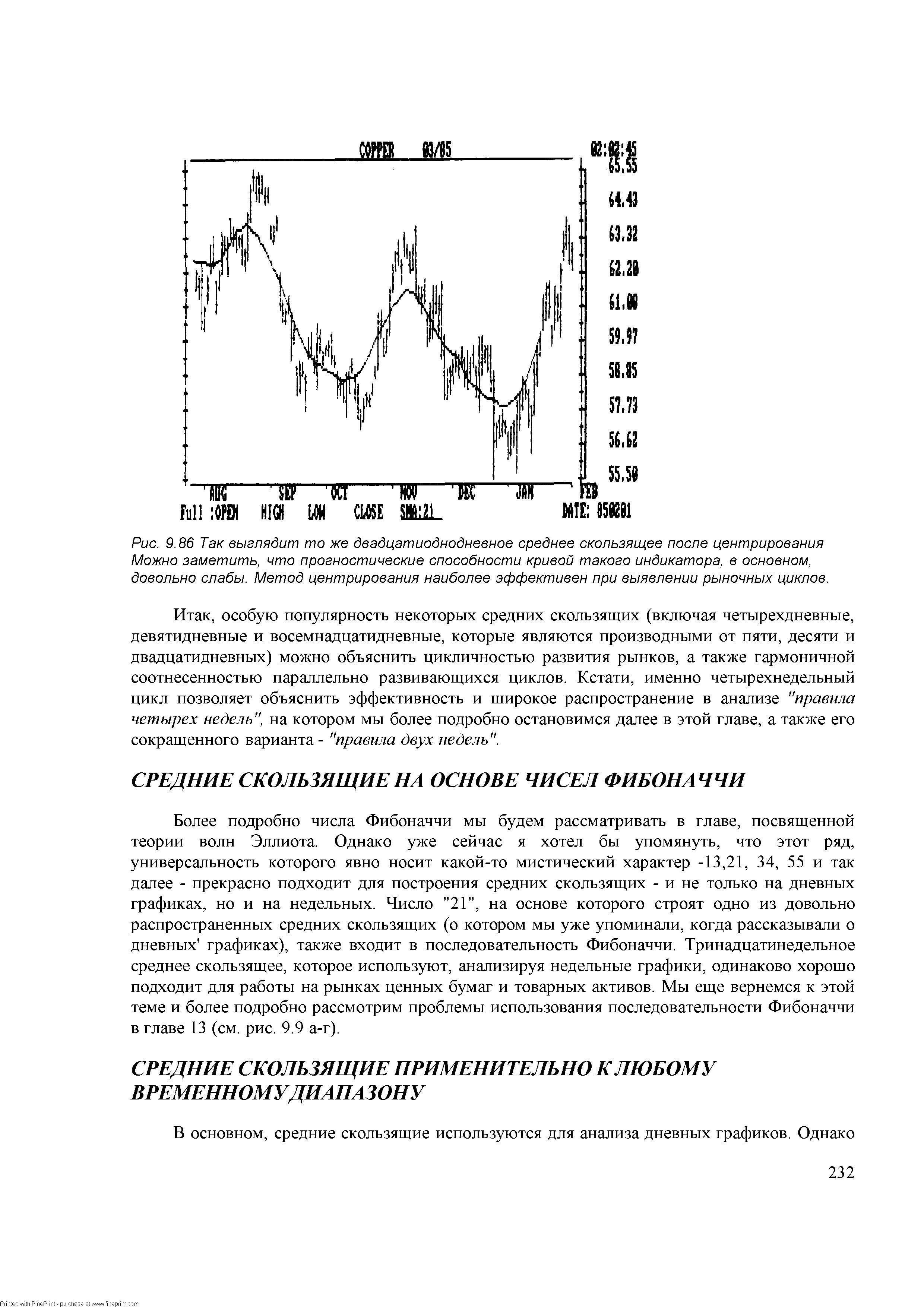 |
| Рис. 14. 20г Пример того, как с помощью двадцатидневного центрированного среднего скользящего значительно облегчается выявление шестнадцатидневного цикла. (Сокращая период расчета среднего скользящего, можно добиться значительного повышения чувствительности графика со снятой направленностью.) Таким образом выделяются циклы, протяженность которых более или менее совпадает с периодом среднего скользящего. | 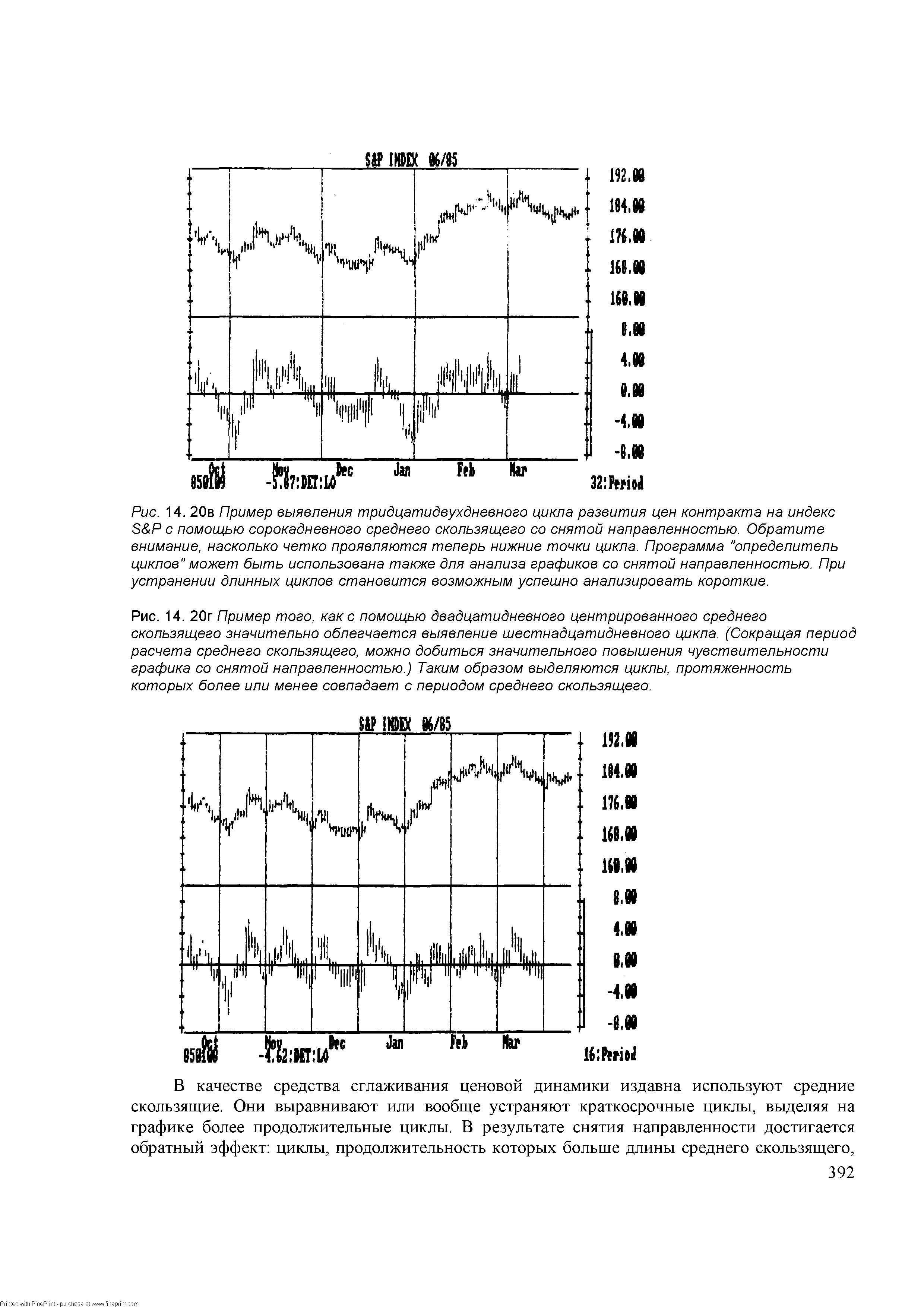 |
