Значение коэффициента парной корреляции изменяется в пределах от -1 до +1. Знак + означает наличие прямой связи между показателями. Знак - — наличие обратной связи. Значение коэффициента от 0 до 1 характеризует степень приближения корреляционной зависимости между показателями и к функциональной. При р = 1 между показателями существует функциональная связь. При р = 0 линейная связь отсутствует. В целях упрощения расчетов на практике применяются и другие формулы коэффициента парной корреляции, представляющие собой некоторые преобразования исходной формулы. [c.280]
Корреляционная зависимость между названными показателями определяется при помощи группировки, которая позволяет выявить характер связи (прямая или обратная). Однако количественно измерить соотношение между объемом товарооборота и производительностью труда торговых работников можно лишь на основе корреляционного анализа. [c.305]
Параметры уравнения могут быть найдены рассмотренными выше способами. После нахождения параметров путем потенцирования, т. е. действия, обратного логарифмированию, переходят к искомому уравнению (1.37). Пример вывода формулы степенной корреляционной зависимости см. на стр. 83. [c.47]
Сущность корреляционной связи состоит в том, что "разным значениям одной переменной соответствуют различные средние значения другой. С изменением значения признака X закономерным образом изменяется среднее значение признака Y..." [21, с. 192]. Проецируя данное положение на финансовую отчетность, можно в принципе вывести взаимосвязи между всеми статьями, установив направление и тесноту связи. Например, в ф. № 1 "Бухгалтерский баланс" и ф. № 2 "Отчет о прибылях и убытках" между строкой 210 "Запасы"(ф. № 1) и строкой 010 "Выручка..."(ф. № 2) существует положительная (прямая) связь, теснота которой (значение коэффициента детерминации от 0 до 0,33 от 0,33 до 0,67 от 0,67 до 1) зависит от количественных значений, а между строкой 020 "Себестоимость..." (ф. № 2) и строкой 010 "Выручка..." (ф. № 2) существует отрицательная (обратная) связь (в обоих случаях элиминировано влияние прочих факторов). Однако устанавливать корреляционную зависимость следует не по формам отчетности, а на основании данных синтетического учета. Полученные результаты послужат подтверждением правильности данных финансовой отчетности. [c.31]
Коэффициент корреляции может принимать любые значения от 0 до 1. Если коэффициент корреляции равен нулю, то это означает отсутствие связи между х и у. Если его абсолютная величина составляет единицу, то, следовательно, существует полная зависимость между исследуемыми факторами, т, е, корреляционная зависимость совпадает с функциональной. Чем ближе коэффициент корреляции к единице, тем теснее зависимость между х и у чем ближе к нулю, тем связь слабее. Положительное значение коэффициента корреляции указывает на прямую зависимость, отрицательное значение — обратную. [c.115]
При изучении корреляции многих переменных могут встретиться как прямолинейные, так и криволинейные зависимости. Как правило, при наличии криволинейной зависимости стремятся преобразовать переменные функции и таким способом подойти к прямолинейной зависимости. Чтобы провести такое преобразование, рассматриваются не сами переменные, а некоторые их функции (логарифмы, обратные величины и т. д.). Например, корреляционная зависимость характеризуется следующим уравнением [c.124]
Анализ корреляционной зависимости экономических показателей от отдельных факторов более сложен. Степень влияния таких факторов при анализе определяется с помощью методов корреляции. Связь между корреляционным фактором и результативным показателем характеризуется прежде всего коэффициентом корреляции, который может изменяться от нуля до единицы. Чем ближе он к единице, тем теснее связь между анализируемыми показателями. Коэффициент корреляции с плюсом указывает на прямую связь, а с минусом — на обратную. Коэффициент корреляции вычисляют по формуле [c.43]
Факторы могут находиться во взаимной связи и взаимозависимости. Существуют два вида связи между взаимодействующими факторами и между факторами и показателями. Проще всего изучать функциональную, т, е. прямую или обратную зависимость, называемую также полной связью. Более сложной для исследования представляется корреляционная зависимость, называемая также неполной или частичной связью. Примером первого вида зависимости является связь между ценой товара и выручкой за товар. Примером второго — зависимость между иеной товара и его качеством. [c.23]
Регрессионный анализ - один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, х[,х2,...,хп у должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида [c.101]
При построении параметрических рядов машин, как и при любом экономическом анализе, недостаточно дать направление влияния (прямая, обратная связь) отдельных факторов на величину затрат, а необходимо знать и количественную сторону этого влияния. Конструкторы, чтобы изучить характер и степень влияния одних факторов на другие, производят наблюдения или опыт, измеряя значение одного фактора при разных значениях другого при условии постоянства значений прочих факторов. Экономист практически лишен возможности провести такой опыт. Поэтому только глубокий анализ отчетных и плановых данных позволяет ему выявить формы связи и степень влияния между факторами. Такой анализ может быть проведен с помощью методов математической статистики, а именно с помощью корреляционного анализа, который позволяет определить форму и степень влияния (тесноту связи) как отдельных факторов (в случае исследования парной зависимости), так и групп факторов (при исследовании множественной зависимости на исследуемую величину). [c.48]
Корреляционные связи в зависимых переменных не могут быть жесткими и носят характер неполных связей. Если в случае увеличении (или уменьшении) аргумента результирующий показатель (функция) также увеличивается (или соответственно уменьшается), то корреляционная связь называется прямой (положительной), а если наоборот — обратной (отрицательной). При отсутствии какой-либо зависимости функции от аргумента, корреляционная связь отсутствует. [c.230]
| Рисунок 3.9. Проекция Саммона 82 инвестиционных фондов, специализирующихся на инвестициях в развивающиеся рынки Исследование взаимосвязи между управленческим стажем менеджеров и оборачиваемостью активов выявило обратную корреляционную зависимость, означающую, что для фондов, управляемых менеджерами с шньшим стажем, характерна более высокая оборачиваемость (группы I и 111 в сравнении с группами II, IV и V) | 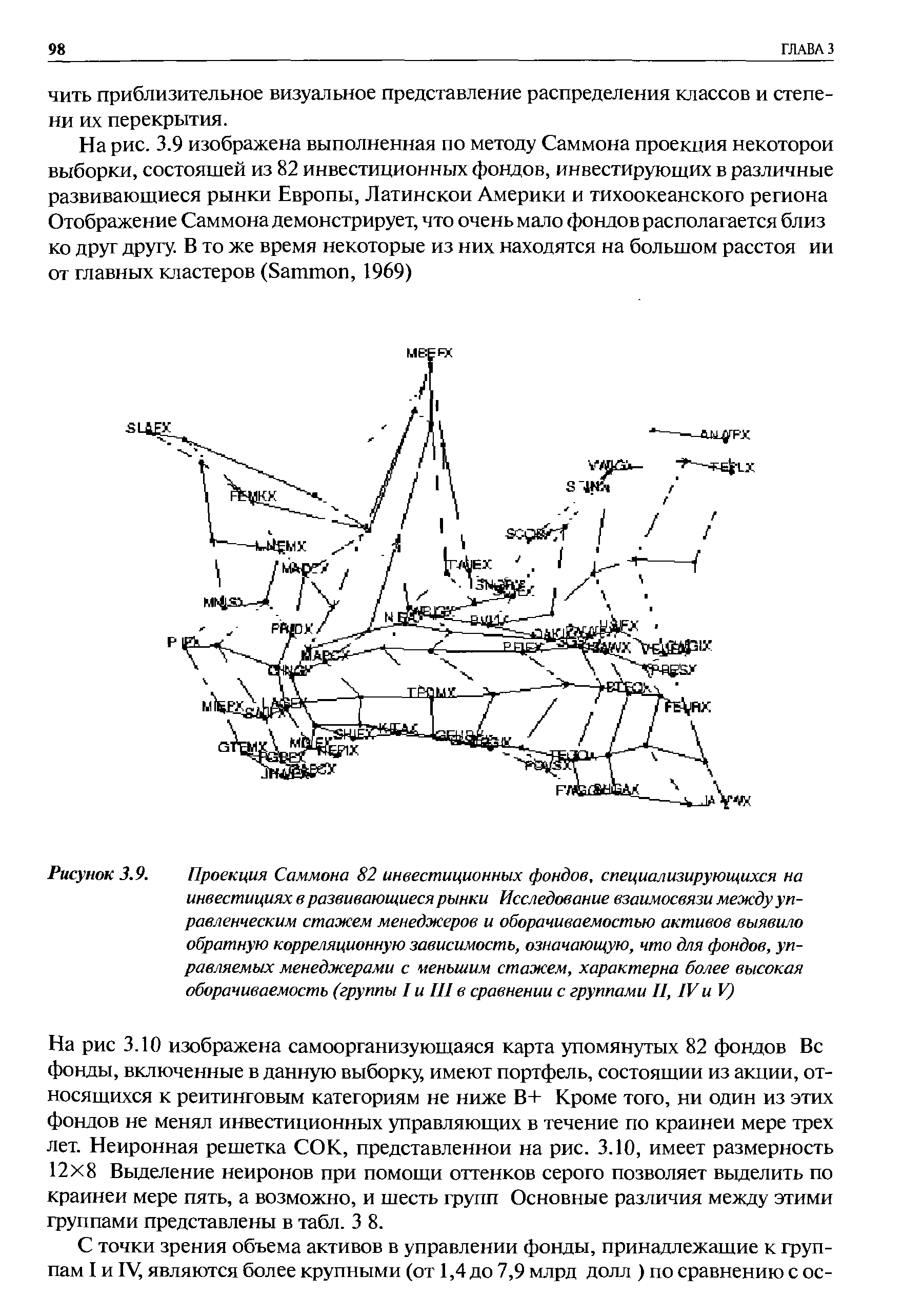 |
Самое большое стандартное отклонение внутри для всех трех групп имеет переменная "возраст". Объединенная межгрупповая корреляционная матрица указывает на некоторую корреляцию переменных и "размер семьи" с "доходом". Переменная имеет отрицательную корреляцию с "путешествием" (т.е. зависимость между путешествием и возрастом обратная). К тому эти корреляции находятся в нижнем ряду, указывая, что хотя муль-неарность и может иметь место, но она, вероятно, вызовет серьезной проблемы. Значимость соответствующих одномерных (отношений межгрупповой суммы квадратов к внутри указывает, что когда предикторы рассматриваются по отдельности, то при дифференциации двух групп только доход и путешествие значимы. [c.702]
Современная аналитическая наука имеет в своем арсенале достаточное число методов и моделей, с помощью которых исходные данные можно подвергать некоторой аналитической обработке с целью выявления закономерностей и тенденций, присущих этим данным или тем явлениям, которые они характеризуют (один из вариантов классификации приемов и моделей анализа деятельности фирмы см. в [Ковалев, 2001, с. 63-68]). В зависимости от вида анализа, поставленных целей, имеющейся информационной базы, различных ограничений, например по времени и инструментарию, могут применяться методы той или иной сложности, тех или иных апалитико-поз-навательных возможностей и др. Так, для выявления тенденции изменения выручки от продаж можно воспользоваться аппаратом корреляционно-регрессионного анализа (чисто инструментальный метод), а можно привлечь экспертов с последующим усреднением приведенных ими оценок (в этом случае имеет место комбинирование неформализованных и формализованных методов анализа). В данной главе мы рассмотрим лишь те методы, которые, на наш взгляд, представляются наиболее практичными при этом мы исходим из предпосылки, что сложность выбираемого метода или модели должна быть адекватной целям и имеющемуся информационному сырью. Говоря об адекватности, мы имеем в виду следующее сложность аналитического инструментария не всегда способствует получению более обоснованных и практичных выводов. В подтверждение приведем два примера. Для любого аналитика при известных навыках не составляет труда построить многофакторную жестко детерминированную модель для выявления причинно-следственных связей между показателями, однако неоправданное усложнение модели может иметь обратный эффект - полученные результаты будут в практическом плане бесполезными. Можно строить регрессионное уравнение по множеству из трех-четырех точек, однако прогностическая ценность подобного уравнения будет близка к нулю, а пользователь, которому будет предложена эта модель как инструмент прогнозирования, не будет испытывать ничего иного, кроме раздражения от ее бесполезности и бессмысленной наукообразности. [c.177]
