Цена акции ( ) Цена опциона ( ) Дельта опциона Гамма опциона [c.128]
К этому моменту читатель уже знает, каким образом время и волатиль-ность влияют на опционы колл, поэтому он в состоянии догадаться и об их влиянии на опционы пут. Как и в случае с опционами колл, течение времени и/или падающая волатильность приводят к тому, что кривая цены опциона пут начинает передвигаться ближе к изогнутой границе истечения срока. Совсем не обязательно нужно руководствоваться математической моделью, чтобы понять, как течение времени влияет на цены, дельты и гаммы опционов пут. Воздействие становится очевидным по мере перемещения кривых все ниже и ниже. Рисунок 6.3 показывает, как цены и ценовые чувствительности опциона пут меняются с течением времени. [c.130]
Мы можем применить эту аргументацию к еще одному, последнему параметру и выявить гамму опциона пут из гаммы опциона колл. Вспомните, что гаммой опциона является скорость изменения дельты, поэтому мы можем это применить к уравнению (6.10) следующим образом [c.143]
С этого мы и начали. Гаммы опционов пут и колл при одинаковых условиях идентичны, поэтому торговцы волатильностью рассматривают оба инструмента одинаково. Все из вышеперечисленных взаимосвязей, состоящих из цены, дельты и гаммы опционов пут, основывающихся на показателях опционов колл, возникают из утверждения, что устойчивая прибыль может быть получена только в том случае, если связи будут нарушены. [c.143]
Таблицы и Рисунки, полученные с помощью этого метода, показывают, как цена опциона, дельта, вега и т.д. изменяются относительно цены базовой акции. Совсем нетрудно показать, как эти свойства изменяются относительно любой другой переменной. Вводя различные значения волатильности, скажем 8%, 9%, 10%.., внутри диапазона (J12...J25) и указывая. значение в С6 (ячейка для ввода волатильности), можно увидеть, как все вышеуказанные результирующие значения зависят от волатильности данной акции. Рисунок А.2 показывает, как цена, дельта и гамма опциона колл изменяются вместе с волатильностью. [c.214]
С изменением условий на рынке величина гаммы также будет меняться. Гамма достигает наибольшей величины для опционов без выигрыша и уменьшается по мере того, как опцион все больше становится с выигрышем или проигрышем (см. рис. 77). Значение гаммы меняется с течением времени и вследствие изменения стандартного отклонения цены актива (см. стр. 78). Как следует из графиков, гамма опциона без выигрыша может резко возрасти при уменьшении времени до истечения контракта и уменьшении дисперсии цены актива. [c.215]
Пример. Инвестор сформировал дельта нейтральный портфель, гамма которого равна 120. Гамма опциона (100 акций) равна 1,2. Портфель будет гамма нейтральным, если инвестор откроет короткую позицию по 120 1,2 = 100 опционам. [c.216]
| Таблица 15.1 Гамма опционов на USD/СНГ с разными сроками и дельтами (%) |  |
Гамма показывает уровень риска опционной позиции. Высокая величина гаммы означает повышенный риск, поскольку стоимость опционного контракта может измениться быстрее. Но иногда, в зависимости от конкретной стратегии, высокий риск более предпочтителен. [c.143]
| Рисунок 4.8 Изгиб цены опциона — гамма | 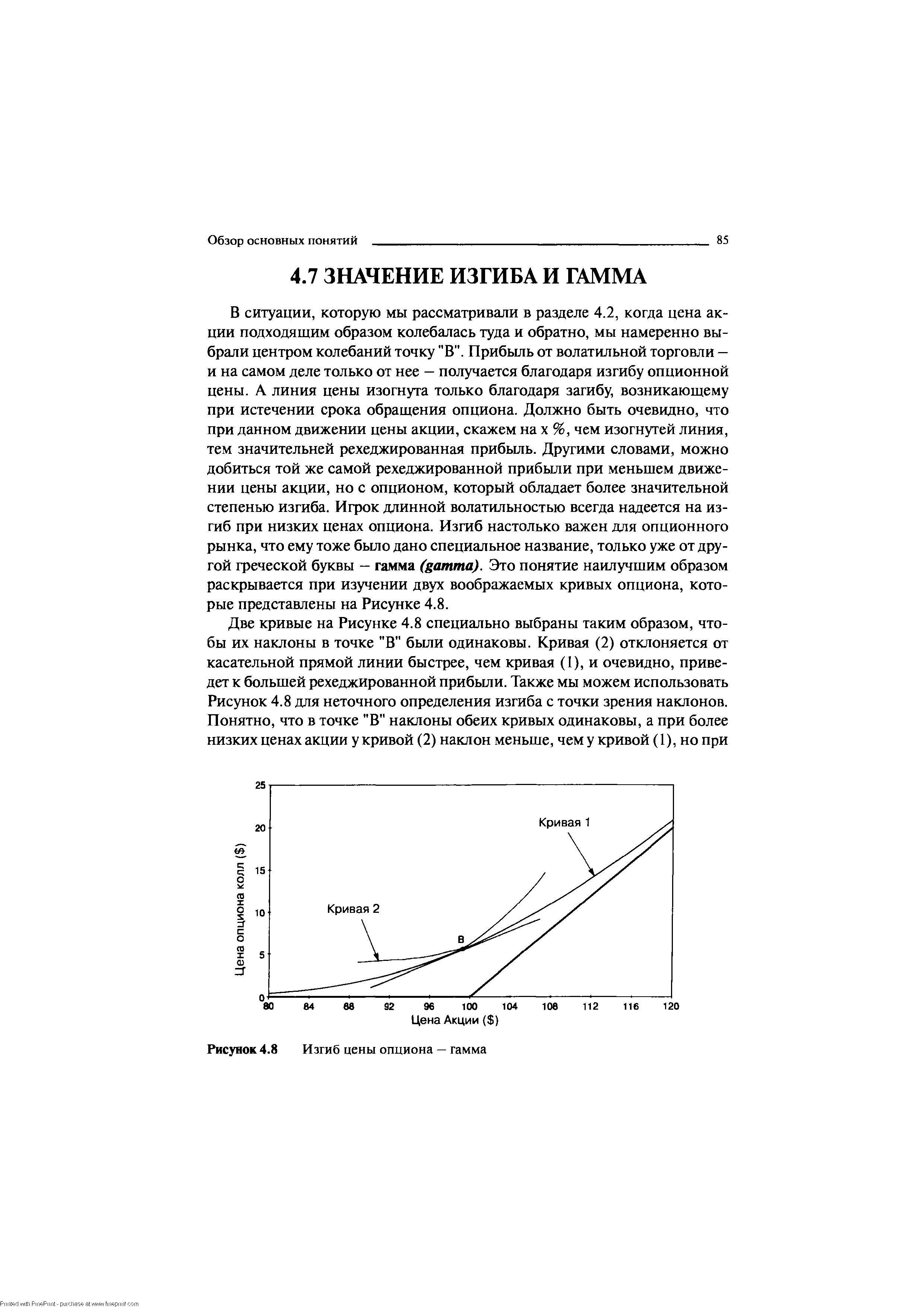 |
Цена Акции ( ) Рисунок 4.9 Цена опциона — дельта — гамма [c.87]
Посмотрим на строку 80, описывающую вывод значения гаммы. При этой цене 100 опционов требуют коротких позиций на 789 акций, чтобы полностью достичь дельта-нейтрального положения. При этой цене гамма равна 12,3 единицам, и маленькие ценовые изменения в 0,10 потре- [c.87]
| Таблица 4.5 Гамма одногодичного опциона колл | 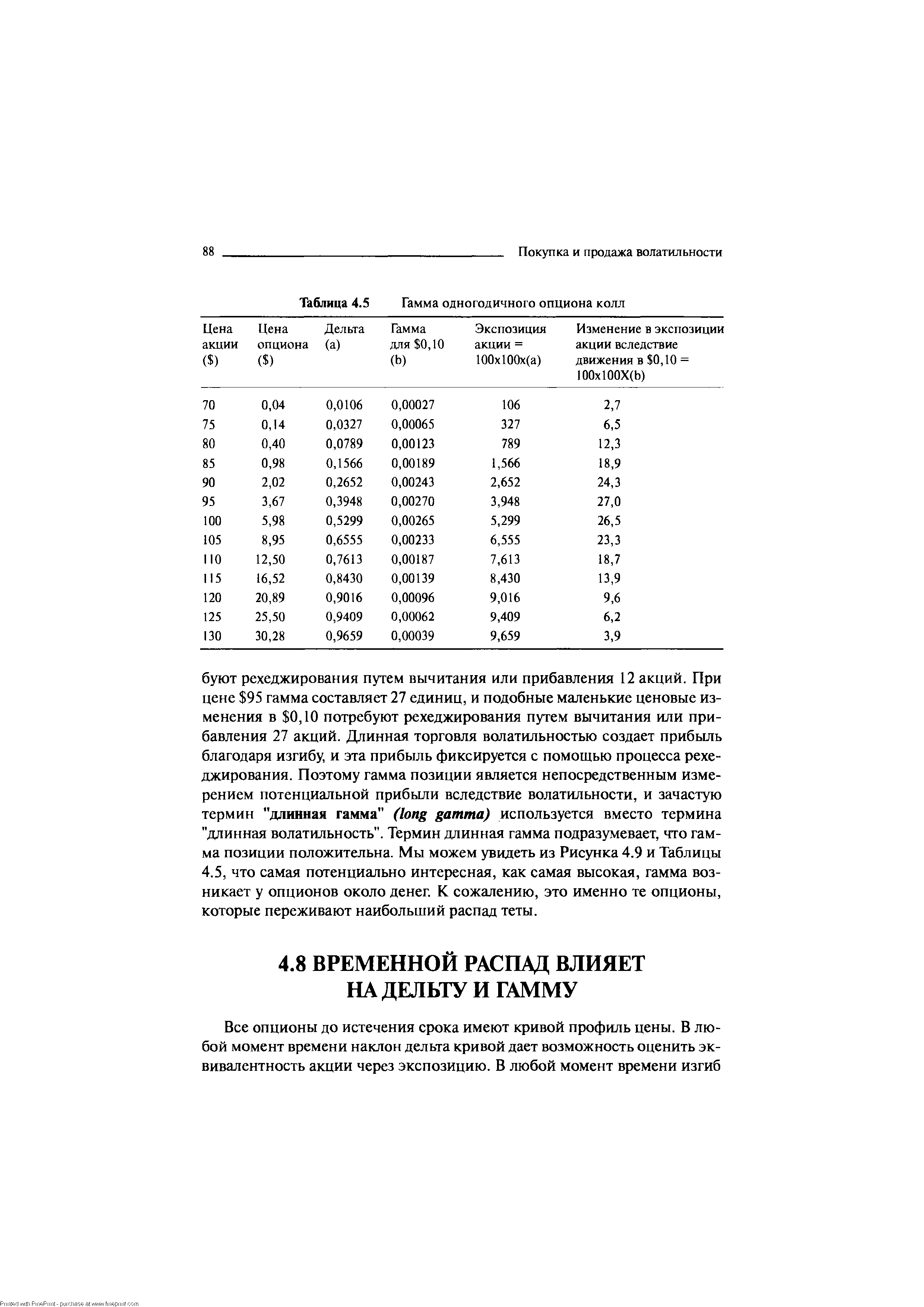 |
Течение времени приводит к постепенному увеличению наклона кривой. К моменту истечения срока опциона кривая совпадает с линией паритетности. В пределе дельта достигает 1,0 и опцион становится неотличимым от акции. Изгиб также постепенно уменьшается. Поэтому длинная волатильная позиция, находясь в деньгах и приближаясь к своему сроку истечения, приводит к постепенному увеличению степени хеджа акции до тех пор, пока при наступлении срока длинная и короткая позиции не совпадут друг с другом один к одному. Как и в случае с опционами без денег, при подходе срока истечения гамма уменьшается, поэтому и наклон рехеджирования тоже уменьшается. [c.90]
Самый интересный аспект опционов около денег при истечении срока заключается в том, что изгиб увеличивается по мере приближения все ближе и ближе к последнему изгибу, в результате чего наклон рехеджирования увеличивается. Таблица 4.6 перечисляет максимальные точки изгиба для различных опционов, представленных на Рисунке 4.10. При сроке в один год до истечения опциона максимальная гамма составляет 27 и соответствует цене 97. Когда остается одна неделя до срока истечения, она увеличивается до 192 и соотносится уже с ценой 99,8. При годовом сроке до истечения ценовое изменение на 0,10 потребует рехеджирования 27 акциями, но при одной неделе до срока истечения то же самое ценовое движение потребует 192 акции. Оканчивающие свой срок жизни опционы в состоянии около денег имеют большие гаммы, и это потому, что дельта может колебаться от 0,0, когда опцион совсем немного без денег, до 1,0, когда опцион немного в деньгах. В качестве экстремального случая рассмотрим опцион, заканчивающийся через минуту. Почти при любой цене, ниже 100, скажем 99,5, опцион должен быть абсолютно нечувствительным к ценовым изменениям акции, его дельта будет 0,0. Поч- [c.90]
Эти выводы подкрепляются графиками цен, дельты и гаммы различных опционов в трех "окошках" на Рисунке 4.11. [c.91]
Другим способом показать изменения дельты и гаммы во времени является карта контура дельты. На Рисунке 4.12 отмечены точки, определяющие цены акции в привязке к временной карте, на которой дельты опционов имеют фиксированные значения. Для ясности мы показываем [c.91]
Во всех вышеперечисленных ситуациях мы предполагали, что параметр волатильности, используемый профессионалами рынка, оставался фиксированным на протяжении всей жизни опциона. Но чаще всего так не бывает. В середине жизни опциона участники рынка могут вдруг осознать, что будущая волатильность собирается падать. В такой ситуации, при прочих равных условиях цена опциона будет придерживаться нижней кривой. Это показано на Рисунке 4.6, и на основании тщательного исследования кривых можно сделать вывод, что изменения в дельте и гамме вследствие движений волатильности почти сходны с изменениями, происходящими под влиянием времени. [c.97]
Опционы далеко без денег будут иметь уменьшающиеся дельты и уменьшающиеся гаммы. [c.98]
Опционы глубоко в деньгах будут иметь увеличивающиеся дельты и уменьшающиеся гаммы. [c.98]
Опционы около денег будут иметь увеличивающиеся гаммы. [c.98]
Опционы далеко без денег будут иметь увеличивающиеся дельты и увеличивающиеся гаммы. [c.98]
Опционы глубоко в деньгах будут иметь уменьшающиеся дельты и увеличивающиеся гаммы. [c.98]
Понимание всех сложностей влияния цены акции, времени до истечения срока действия опциона и волатильности на цену опциона, дельту и гамму является существенным моментом в управлении волатильной стратегией. Простая длинная стратегия волатильности может принести прибыль при хороших обстоятельствах, равно как и убыток при плохих обстоятельствах. Хорошие обстоятельства — это покупка опционов с относительно низкой подразумеваемой волатильностью, а в последующем - развитие ситуации с высокой волатильностью. Это может означать покупку 25% волатильности и получение в дальнейшем 35% волатильности [c.98]
Величина гамма (у) измеряет, насколько изменится дельта опциона при малом изменении цены акции. Следовательно, гамма опциона — это вторая производная его цены по цене основной акции. Гамма, как правило, бывает большой для at-the-money опционов. Эта величина показывает, насколько существенное уточнение позиций по опционам происходит при изменении цены акций. Большое значение у говорит о том, что изменение цены акций вызовет большие изменения в позициях по опционам. Такое уточнение позиций может повлиять на интенсивность торгов и на цену, поэтому изменения величины гамма имеют определенное значение для прогнозирования объема торговли и цен на рынке акций. [c.126]
Вы будете получать прибыль на движении курса spot и нести убытки на изменении волатильности. Поскольку курс spot растет, у вас будет длинная гамма, т.к. гамма опциона пут, который вы продали, будет уменьшаться, а гамма опциона кол, который вы купили, будет расти. То же самое будет происходить и с вегой. Однако, чем меньше неопределенности на рынке по поводу направления движения, тем ниже ожидаемая волатильность. Таким образом, поскольку ваша позиция становится более положительной в терминах веги, а волатильность снижается, вы начинаете терять деньги на веге и тете, в то время как выигрываете на гамме. Это объяснение относится к захеджированным позициям. [c.209]
Трейдеры могут быть не в состоянии гарантировать цены рынках спотов, необратимых форвардов или фьючерсов, временно оставляя позицию Дельта не застрахованной (unhedged). Чтобы избежать высокой стоимости страховки и риска наступления необычно высокой волатильности, трейдер может застраховать позиции исходного опциона другими опционами. Такие методы нейтрализации риска называются страхоками Гамма или Вега . [c.34]
Гамма (Г) известна также как искривление опциона ( urvature of the option). Это вторая производная модели ценообразования опциона (МЦО) и представляет собой степень изменения Дельты опциона, или чувствительность Дельты . Например, опцион с А=0.5 и Г=0.05 предположительно должен иметь А=0.55, если цена валюты поднимется на 1 очко, или А=0.45, если цена упадет на 1 очко. Гамма изменяется в пределах от 0 до 100%. Чем выше Гамма , тем выше чувствительность Дельты . Поэтому может оказаться целесообразным трактовать Гамму как показатель ускорения опциона по отношению к движению валюты. [c.34]
Использование фьючерсов в рамках данной тактики осложняется тем, что рынок фьючерсов не следует точно за наличным рынком. Далее, портфель, против которого вы продаете фьючерсы, может не вполне точно отслеживать сам индекс, лежащий в основе фьючерса. Такой дисбаланс может внести свой вклад в неустойчивость страхования портфеля. Более того, когда имитируемый опцион очень близко подходит к сроку своего истечения и стоимость портфеля приближается к цене исполнения, гамма этого опциона астрономически вырастает. Гамма — это текущая скорость изменения дельты, или степени хеджирования. Другими словами, гамма — это дельта дельты. Когда дельта изменяется очень быстро (т. е. если имитируемый опцион имеет высокую гамму), проведение страхования портфеля все больше осложняется. Есть множество способов справиться с этой проблемой, некоторые из которых весьма изощренные. Один из простейших опирается на концепцию бессрочного опциона. Вы, например, всегда можете предположить, что опцион, который вы имитиру- [c.223]
В ситуации, которую мы рассматривали в разделе 4.2, когда цена акции подходящим образом колебалась туда и обратно, мы намеренно выбрали центром колебаний точку "В". Прибыль от волатильной торговли — и на самом деле только от нее — получается благодаря изгибу опционной цены. А линия цены изогнута только благодаря загибу, возникающему при истечении срока обращения опциона. Должно быть очевидно, что при данном движении цены акции, скажем на х %, чем изогнутей линия, тем значительней рехеджированная прибыль. Другими словами, можно добиться той же самой рехеджированной прибьыи при меньшем движении цены акции, но с опционом, который обладает более значительной степенью изгиба. Игрок длинной волатильностью всегда надеется на изгиб при низких ценах опциона. Изгиб настолько важен для опционного рынка, что ему тоже было дано специальное название, только уже от другой греческой буквы — гамма (gamma). Это понятие наилучшим образом раскрывается при изучении двух воображаемых кривых опциона, которые представлены на Рисунке 4.8. [c.85]
Точным математическим определением гаммы является мгновенная скорость изменения дельты. На практике легче всего рассматривать изменения дельты, вызванные небольшими изменениями цены акции. Реальная польза гаммы для опционного трейдера и игрока волатильностью — в оценке будущих результатов рехеджирования. Гамма является изменением дельты, связанной с изменением цены базового инструмента, поэтому гамма также является способом измерения скорости, с которой мы рехеджируем дельта-нейтральную позицию. Таблица 4.5 демонстрирует ситуацию с портфелем, содержащим 100 опционов. Каждый опцион может быть исполнен на 100 акций, поэтому для этого портфеля все дельты и гаммы помножены на 100x100=10.000. Мы произвольно определяем здесь гамму, основываясь на изменении в дельте, которое происходит при движении в 0,10 в базовом инструменте. [c.86]
Цена акции ( ) Цена опциона ( ) Дельта (а) Гамма для 0,10 (Ь) Экспозиция акции = ЮОхЮОх(а) Изменение в экспозиции акции вследствие движения в 0,10 = ЮОхЮОХ(Ь) [c.88]
Для игрока длинной волатильностью это может быть или хорошей, или плохой новостью. Какова бы ни была ситуация, портфель будет переживать немедленную переоценку потерь вследствие падения цены опциона. Однако если цена акции близка к цене исполнения, тогда увеличение гаммы фактически может означать больший простор для рехеджи-рования, чем раньше. Несмотря на то, что могут возникнуть и первоначальные убытки, они способны быть больше, нежели компенсация от возросшей вероятности будущего рехеджирования. Мы говорили о спаде в волатильности. А что произойдет, если будет наблюдаться неожиданный подъем волатильности [c.98]
