Вычислим структурные коэффициенты модели [c.110]
Определите структурные коэффициенты модели. [c.134]
Структурная форма модели в правой части содержит при эндогенных и экзогенных переменных коэффициенты bt и о, (й, — коэффициент при эндогенной переменной, о, - коэффициент при экзогенной переменной), которые называются структурными коэффициентами модели. Все переменные в модели выражены в [c.181]
Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели. [c.182]
Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели ввиду слабой взаимосвязи признаков с эндогенной переменной из левой части системы равны нулю. Тем самым уменьшится число структурных коэффициентов модели. Так, если предположить, что в нашей модели а13 = 0 и а21 = 0, то структурная модель примет вид [c.186]
В такой модели число структурных коэффициентов не превышает число коэффициентов приведенной модели, которое равно 6. Уменьшение числа структурных коэффициентов модели [c.186]
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема. Рассмотренная выше структурная модель (4.4) с двумя эндогенными и тремя экзогенными (предопределенными) переменными, содержащая шесть структурных коэффициентов, представляет собой идентифицируемую модель. [c.187]
Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной Pi = 8п хх + да х2 +. .. + 8у Xj и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных. [c.200]
Определяются структурные коэффициенты модели по данным [c.33]
Одним из случаев успешного применения МНК для оценки структурных коэффициентов модели является его использование для рекурсивных (треугольных) моделей. В этих моделях эндогенные переменные последовательно (рекурсивно) связаны друг с другом. А именно, первая эндогенная переменная YI зависит лишь от экзогенных переменных Хь i = 1, 2,. .., m и случайного отклонения Si. Вторая эндогенная переменная Y2 определяется лишь значениями экзогенных переменных Х i = 1, 2,. .., m случайным отклонением 82, а также эндогенной переменной YI. Третья эндогенная переменная Y3 зависит от тех же переменных, что и Y2, случайного отклонения з, а также от предыдущих эндогенных переменных (Yi, Y2) и т. д. [c.326]
| Рис. 1.4. Структурно-логическая модель факторной системы коэффициента текущей ликвидности. |  |
| Рис. 1.5. Структурно-логическая модель факторной системы коэффициента прибыльности общих активов. | 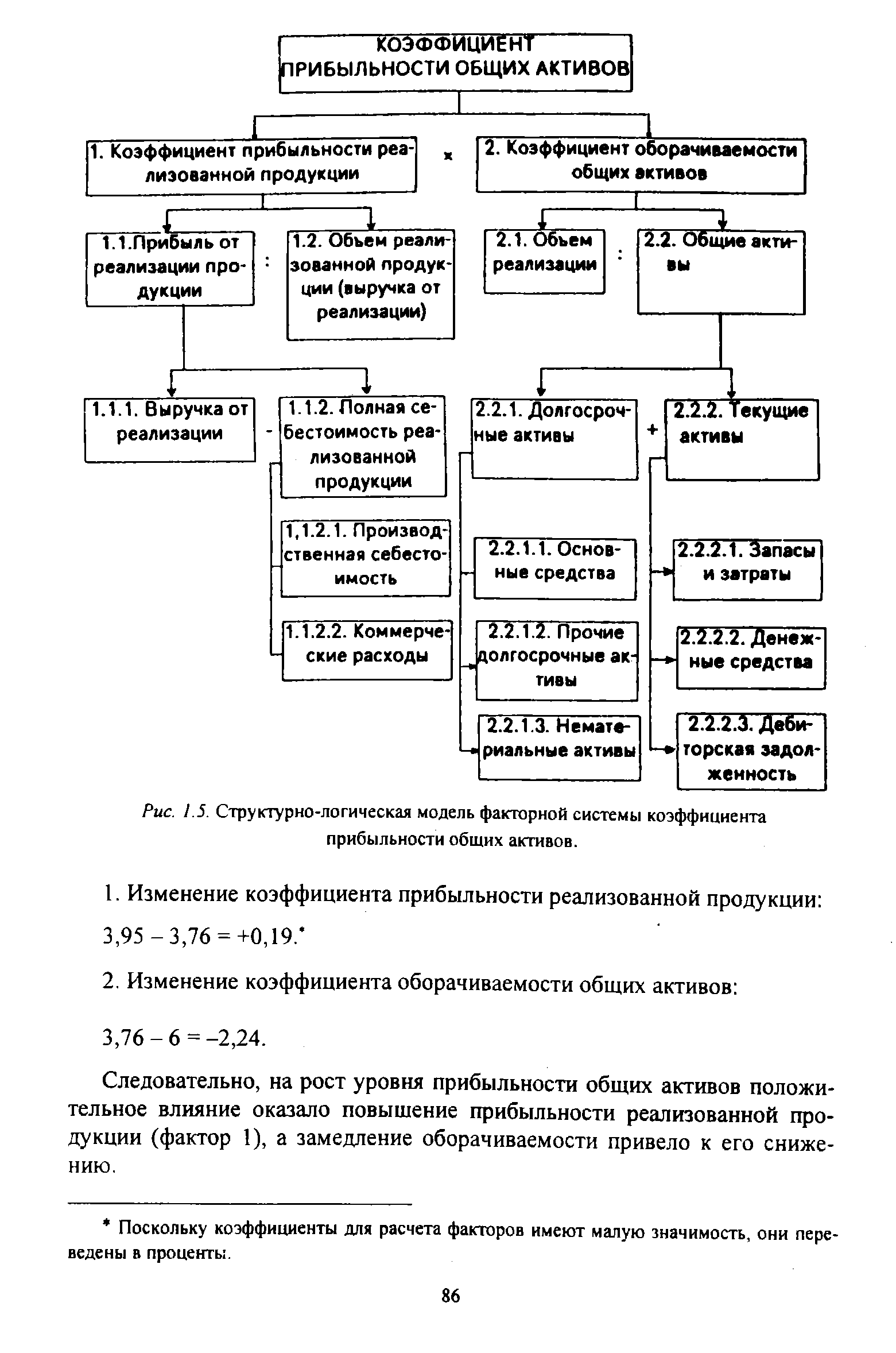 |
Какие структурные параметры модели можно найти через приведенные коэффициенты. Ответ обоснуйте. В качестве примера найдите параметры какого-либо одного структурного уравнения. [c.134]
Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели (5/j) через коэффициенты структурной модели Ц- и bt). Для упрощения в модель не введены случайные переменные. [c.182]
Из уравнения следует, что коэффициенты приведенной формы модели представляют собой нелинейные соотношения коэффициентов структурной формы модели, т. е. [c.183]
Аналогично можно показать, что коэффициенты приведенной формы модели второго уравнения системы (<521 и Ь 2) также нелинейно связаны с коэффициентами структурной модели. Для этого выразим переменную ух из второго структурного уравнения модели как [c.183]
Она позволяет получить значения эндогенной переменной с через переменную х. Рассчитав коэффициенты приведенной формы модели (Aq, А,, Во, В,), можно перейти к коэффициентам структурной модели аи Ь, подставляя в первое уравнение приведенной формы выражение переменной х из второго уравнения приведенной формы модели. Приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, аналитически уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи между эндогенными переменными. [c.185]
Наличие двух вариантов для расчета структурных коэффициентов одной и той же модели связано с неполной ее идентификацией. Структурная модель в полном виде, состоящая в каждом [c.185]
Как видим, модель содержит восемь структурных коэффициентов, что соответствует выражению я (л — 1 + т). [c.186]
На основе шести коэффициентов приведенной формы модели требуется определить восемь структурных коэффициентов рассматриваемой структурной модели, что, естественно, не может привести к единственности решения. В полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно я (л — 1 + т) параметров структурной модели не могут быть однозначно определены из пт параметров приведенной формы модели. [c.186]
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Структурная модель в полном виде (4.1), содержащая л эндогенных и т предопределенных переменных в каждом уравнении системы, всегда неидентифицируема. [c.187]
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Так, если в структурной модели полного вида (4.1) предположить нулевые значения не только коэффициентов я13 и а21 (как в модели (4.2)), но и а22 — 0, то система уравнений станет сверхидентифицируемой [c.187]
В силу наличия тождества в модели (второе уравнение системы) структурный коэффициент Ь не может быть больше 1. Он характеризует предельную склонность к потреблению. Так, если Ь = 0,65, то из каждой дополнительной тысячи дохода на потребление расходуется в среднем 650 руб. и 350 руб. инвестируется, т. е. С и у выражены в тыс. руб. Если Ь > I, то у < С + I, т. е. на потребление расходуются не только доходы, но и сбережения. Параметр а Кейнс истолковывал как прирост потребления за счет [c.205]
Иначе говоря, проблема идентифицируемости структурных параметров — это проблема достаточности эмпирических данных для оценки всех коэффициентов модели. Необходимым условием идентифицируемости уравнения является отсутствие среди линейных комбинаций оставшихся уравнений, таких, которые удовлетворяли бы всем ограничениям модели, накладываемым на исследуемое уравнение. [c.220]
Модель идентифицируема - если все ее структурные коэффициенты [c.32]
Модель неидентифицируема - если число структурных коэффициентов [c.32]
Структурная форма модели преобразуется в П.ф.м. путем последовательных подстановок, и все коэффициенты параметры) последней представляют собой некоторые функции первоначальных коэффициентов структурной формы модели. [c.280]
| Рис. 25.2. Структурно-логическая модель факторного анализа коэффициента текущей ликвидности | 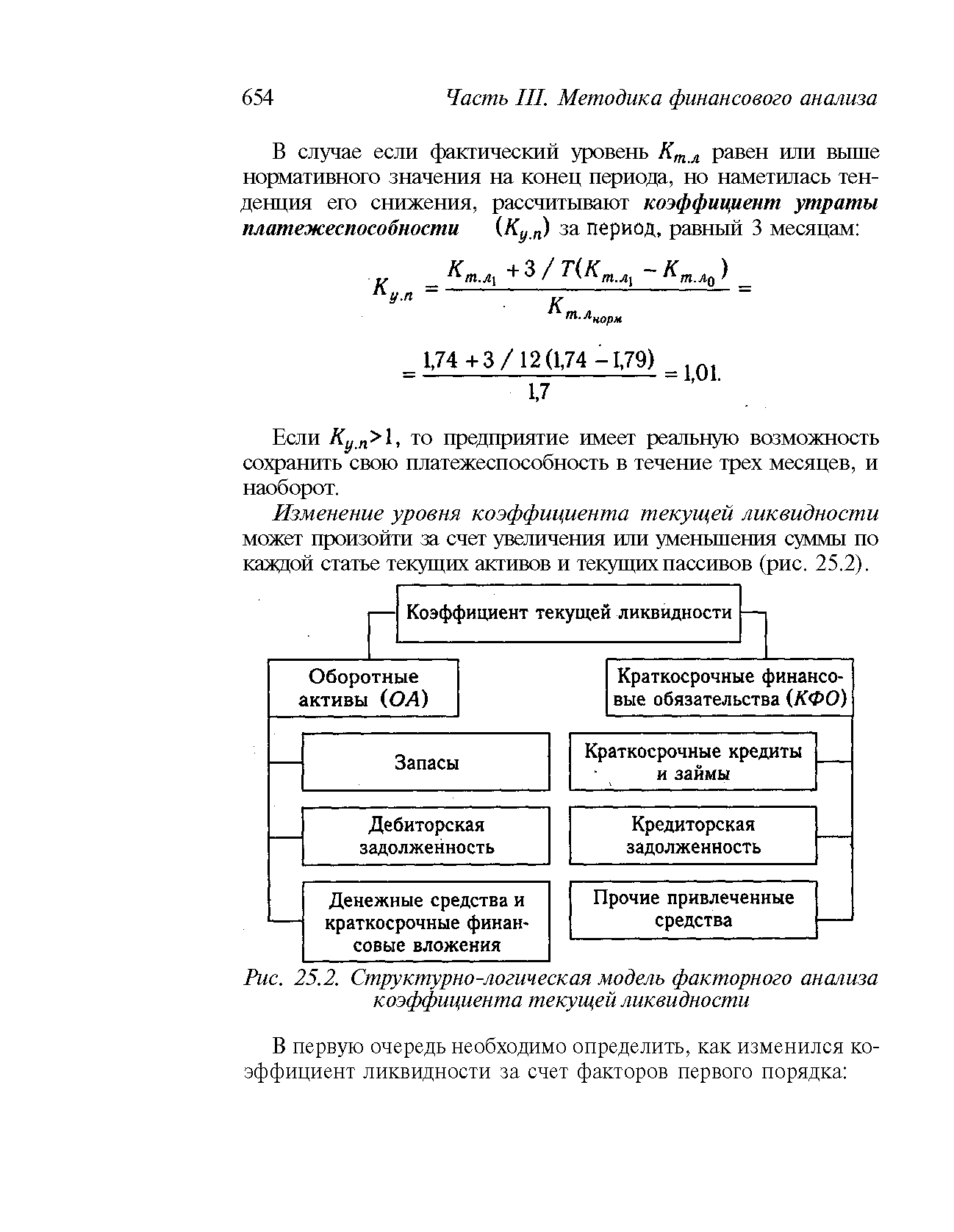 |
Различия между коэффициентами регрессии и структурными коэффициентами модели численно могут быть и менее существенными. Так, например, Г.Тинтнер, рассматривая статическую [c.198]
Очевидно, что выводы, сделанные на основе исследования эколого-экономическои модели региона, имели рекомендательный характер, а достоверность результатов во многом зави-сила от точности определения структурных коэффициентов модели и возможности реализации в ней предположений, положенных в основу того или иного варианта развития. [c.234]
Матрица А имеет порядок G X (G+K) и содержит все структурные коэффициенты модели, а матрица W порядка (G+KJxK, ее ранг равен К-Лервое из уравнений (12.36) можно записать [c.356]
Кроме того, коэффициенты приведенной формы могут быть оценены г тем непосредственного применения обыкновенного метода наименьш квадратов к каждому уравнению приведенной формы в отдельное Этот метод не позволяет принять в расчет какие-либо ограничения коэффициенты приведенной формы, а следовательно, и на структурн коэффициенты модели, т.е. на элементы матриц В и Г. Он известен к метод наименьших квадратов без ограничений. Заметим, что метод нг меньших квадратов без ограничений и обыкновенный метод найме ших квадратов — два разных метода оценивания параметров при] [c.421]
При сравнении результатов, полученных традиционным МНК и с помощью КМНК, следует иметь в виду, что традиционный МНК, применяемый к каждому уравнению структурной формы модели, взятому в отдельности, дает смещенные оценки структурных коэффициентов. Как показал Т. Хаавельмо, рассматривая две взаимосвязанные рефессии [c.199]
Компьютерная программа применения КМНК предполагает, что система уравнений содержит в правой части в каждом уравнении как эндогенные, так и экзогенные переменные. Между тем могут быть системы, в которых в одном из уравнений, например, отсутствуют экзогенные переменные. Так, в п. 4.3 рассматривалась модель экономики страны с четырьмя эндогенными и двумя экзогенными переменными, в которой в первом уравнении системы не содержалось ни одной экзогенной переменной. Для такой модели непосредственное получение структурных коэффициентов невозможно. В этом случае сначала определяется система приведенной формы модели, решаемая обычным МНК, а затем путем алгебраических преобразований переходят к коэффициентам структурной модели. [c.200]
Решение сверхидентифицируемой модели на компьютере построено на предположении, что при каждой переменной в правой части системы имеется свой структурный коэффициент. Если же в модель вводятся ограничения на параметры, как в рассмотренном примере Ьп = ап, то программа DSTAT не работает. Структурная модель может принимать любой вид, но без ограничений на параметры. При этом должно выполняться счетное правило идентификации D + 1 > Н. Так, если структурная модель имеет вид [c.203]
Рассматриваемая модель Кейнса точно идентифицируема, и для получения величины структурного коэффициента Ь применяется КМНК. Это значит, что строится система приведенных уравнений [c.206]
СТРУКТУРНАЯ ФОРМА МОДЕЛИ [stru tural form of a model] — такая форма представления эконометрической модели, в которой в виде уравнений и тождеств записаны закономерные и случайные (стохастические) соотношения между текущими и лаговыми переменными модели, отражающими наблюдаемые исследователем экономические явления и процессы, а также другие ограничения модели и стохастические компоненты (см. Помехи). Коэффициенты уравнений при этом называются структурными коэффициентами. С.ф. для решения модели обычно преобразуется в приведенную форму модели. [c.351]
Модель приведенной формы (redu ed-form of model) — система уравнений, в которой каждая из текущих эндогенных переменных непосредственно выражена как функция предопределенных переменных. Иными словами, каждое уравнение представляет собой решение системы уравнений модели, заданной в структурной форме, относительно каждой текущей эндогенной переменной. Число уравнений модели равно числу текущих эндогенных переменных. Структурная форма модели преобразуется в приведенную путем последовательных подстановок, и все параметры последней представляют собой некоторые функции первоначальных коэффициентов. Например, если структурная модель включает уравнения, объясняющие спрос на деньги и их предложение, то приведенная форма модели содержит только одно уравнение, показывающее, как переменная денег связана с другими показателями, например ценами. [c.196]
Заметим, что если в каждое из структурных уравнений модели "спрос - предложение" наряду с ценой товара будет добавлено по одной объясняющей (экзогенной или предопределенной) переменной (например, it в функцию спроса и pt i в функцию предложения), то коэффициенты структурных уравнений могут быть оценены однозначно. В этом случае модель является однозначно определенной (идентифицируемой). [c.322]
