Здесь ряд yt представлен в виде композиции детерминированной составляющей а + (3t (линейный тренд) и случайной составляющей et, являющейся стационарным временным рядом с нулевым средним. Часто встречаются другие примеры тренда квадратичный, а + j3t + 7 2 экспоненциальный ае 1 и т. п. [c.285]
В разделе 2.7.1 приведены примеры трендов. [c.40]
Id. Пример тренда вверх на часовых свечках [c.42]
| Рис. 7.1. Пример тренда 7.1. Сущность и основные формы трендов | 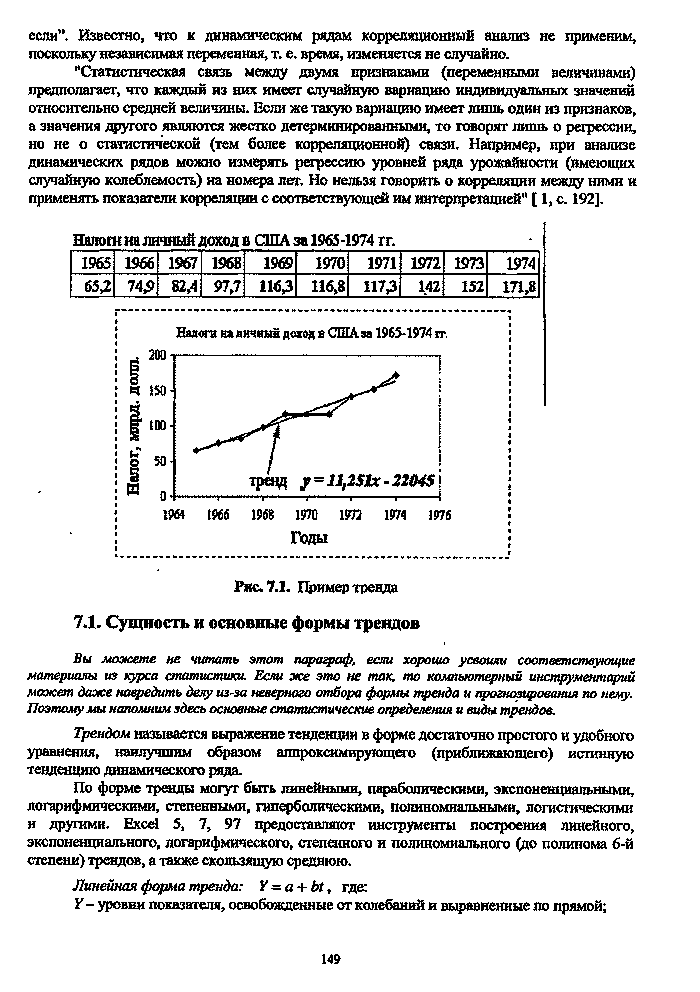 |
Пример 14.6. Построим линейный тренд процентных ставок по кредитам на основе статистических данных, опубликованных в Бюллетене банковской статистики № 4 (47) за 1997 г. [c.612]
Пример 14.7. Предполагая наличие циклических колебаний, проведем гармонический анализ динамики отклонений от линейного тренда данных о ставках по кредитам (у, — у,). [c.617]
Для того чтобы нагляднее представить показатели, характеризующие тенденцию, следует абстрагироваться от колеблемости и выявить динамический ряд в форме чистого тренда при отсутствии колебаний. Пример такого ряда представлен в табл. 9.2. [c.304]
Проверка гипотез о других типах тенденций динамики, рассмотренных в п. 9.4, сложнее и здесь излагаться не будет. Итак, в нашем примере принято решение считать тренд линейным, и следует Приступить к вычислению его параметров. [c.329]
Как видно в табл. 9.4, при вычислении параметров тренда уровни исходного ряда входят с разными весами - значениями // и их квадратов. Поэтому влияние колебаний уровней на параметры тренда зависит от того, на какой номер года приходится урожайный либо неурожайный год. Если резкое отклонение приходится на год с нулевым номером (/, = 0), то оно никакого влияния на параметры тренда не окажет, а если попадет на начало и конец ряда, то повлияет сильно. Следовательно, однократное аналитическое выравнивание неполно освобождает параметры тренда от влияния колеблемости, и при сильных колебаниях они могут быть сильно искажены, что в нашем примере случилось с параболой. Для дальнейшего исключения искажающего влияния колебаний на параметры тренда следует применить метод многократного скользящего выравнивания. [c.334]
Наиболее точную и полную методику анализа с разложением ряда динамики на три компонента тренд, сезонную колеблемость и случайную колеблемость рассмотрим на примере динамики импорта КНР по кварталам за 1993 - 1995 гг. (табл. 9.10). [c.349]
Это означает, что в среднем за период отклонение себестоимости от тренда было противоположно по знаку и составляло 0,124 отклонения урожайности от своего тренда. Если, например, урожайность в 1993 г. окажется на 20 ц/га ниже уровня тренда для этого года, составляющего 119,9 + 3,81 10 = 158 ц/га, то себестоимость надо ожидать на-20 (-0,124) = 2,48 руб. за 1 ц выше уровня тренда, который для 1993 г. равен 31,2 руб. за 1 ц, т. е., учитывая и тренды, и предполагаемый плохой урожай в 1993 г., себестоимость картофеля составила бы 31,2 + 2,48 = 33,66 руб./ц. Естественно, что этот прогноз всего лишь пример, как пользоваться уравнением регрессии отклонений от тренда. В нашем случае метеорология не дает оснований для прогноза урожайности, а сильнейшая инфляция делает вообще невозможным любой прогноз себестоимости без использования дефлятора (см. гл. 10). [c.365]
Другим приемом измерения корреляции в рядах динамики может служить корреляция между теми из цепных показателей рядов, которые являются константами их трендов. При линейных трендах - это цепные абсолютные приросты. Вычислив их по исходным рядам динамики (axl, ayi), находим коэффициент корреляции между абсолютными изменениями по формуле (9.52) или, что более точно, по формуле (9.51), так как средние изменения не равны нулю в отличие от средних отклонений от трендов. Допустимость данного способа основана на том, что разность между соседними уровнями в основном состоит из колебаний, а доля тренда в них невелика, следовательно, искажение корреляции от тренда очень большое при кумулятивном эффекте на протяжении длительного периода, весьма мало - за каждый год в отдельности. Однако нужно помнить, что это справедливо лишь для рядов с с-показателем, существенно меньшим единицы. В нашем примере для ряда урожайности с-по-казатель равен 0,144, для себестоимости он равен 0,350. Коэффициент корреляции цепных абсолютных изменений составил 0,928, что очень близко к коэффициенту корреляции отклонений от трендов. [c.366]
Как видно из графика на рис. 6.3, имеются существенные колебания показателей объема продаж. Однако отмечается видимая тенденция к увеличению объема продаж, и соответствующий тренд можно выделить с помощью методов регрессии. Линия регрессии показана на графике (рис. 6.3). Из графика видно, что зависимость определена не столь четко, как в предыдущем примере. Так, коэффициент корреляции для этих данных будет значительно меньше по величине, и вообще может оказаться незначимым. Долговременный тренд может быть линейным или нелинейным. Эти данные трудно анализировать из-за сильных расхождений между соседними значениями. Часто, когда мы имеем дело с такого рода данными, необходимо сгладить колебания, и только потом можно сделать какой-либо имеющий смысл прогноз. Методы сглаживания данных временных рядов будут более подробно рассмотрены в последующих разделах. [c.188]
При анализе расхождений результатов применения двух сглаживающих констант при выделении тренда следует обратить внимание на два момента. Во-первых, временной лаг, который очевиден при а=0.1, гораздо менее выражен при а=0.3. В целом, чем больше значение при вычислении сглаженных значений, тем последние более чувствительны к изменениям в последних значениях временного ряда. То есть в этом случае сглаженные значения отстают от значений временного ряда не столь сильно, как это происходит при более малых значениях сглаживающей константы. Этот фактор не играет никакой роли, если отсутствует существенное изменение в общем тренде временного ряда. Однако он крайне важен при составлении прогнозов, когда отмечается значимое восхождение или нисхождение общего тренда временного ряда. Значения, полученные в нашем примере при <х=0.3, лучше отражают общий тренд, чем те, которые рассчитаны при а=0.1, что видно из рис. 6.7. [c.195]
Графики, представленные на рис. 6.8, показывают два временных ряда и соответствующие линии тренда. На рис. 6.8 (i) отклонения от тренда относительно постоянны, а на рис. 6.8 (ii) отклонения нарастают по мере восхождения тренда. На этих простых примерах видно, что в первом случае (i) следует применить метод сложения, а во втором (ii) — метод умножения. [c.198]
В этом примере мы рассмотрим ситуацию, когда при вычислении скользящих средних берется четное число значений. В этом случае для определения тренда временного ряда мы будем пользоваться значениями центрированных скользящих средних. В таблице ниже представлены данные по двухмесячному объему производства среднего предприятия обрабатывающей отрасли промышленности, расположенного в Дублине. (Цифры общего объема производства за каждые два месяца даны в тоннах.) [c.203]
Другими словами, сезонную составляющую можно рассчитать путем деления тренда и исходного значения временного ряда. В одном из методов при выделении тренда мы берем скользящие средние. То есть если поделить исходные значения на скользящие средние, то мы получим оценочные значения сезонного отклонения. Все это мы покажем на последующих примерах. [c.206]
Этот пример вновь демонстрирует сильное присутствие сезонной составляющей. Часто на практике трудно решить, какой метод применить сложения или умножения. В принципе, если колебания остаются неизменными, то лучше применять метод сложения. В этом случае, который мы рассматриваем сейчас, колебания увеличиваются по мере восхождения тренда. Давайте рассмотрим размер значений в 1993 г. (100 в мае—августе и 121 в сентябре—декабре) и аналогичный размер в 1997 году (175 в мае—августе и 206 в сентябре—декабре). Мы видим, что внешне разрыв увеличивается, и поэтому можно воспользоваться методом умножения, который в этом случае, вероятно, более приемлем. [c.206]
Выявление циклической составляющей временного ряда может оказаться крайне сложным. И обычно это возможно только тогда, когда имеются данные за продолжительный период времени. Метод сглаживания ряда значений с помощью скользящих средних или экспоненциального сглаживания устраняет сезонные и случайные колебания данных, а оставшиеся значения складываются из тренда и циклических составляющих. Данное пособие не имеет своей целью отдельно рассмотреть вопросы, связанные с циклическими колебаниями. Большинство методов анализа рассматривают тренд и циклические составляющие как единое целое. Однако все же целесообразно проанализировать пример, в котором данные с очевидностью выказывают циклические колебания. [c.210]
В одном из предыдущих примеров мы рассмотрели прогноз по объему производства за два месяца некой компании из Дублина. Были получены оценки на 1997 год, при этом использовался линейный тренд и метод сложения. Прогнозные значения даны в тоннах [c.213]
Точность прогноза однозначно зависит от применяемой модели. Однако, вышесказанное не означает, что при составлении того или иного прогноза приемлема только какая-нибудь одна модель. Вполне возможно, что в ряде случаев несколько различных моделей выдадут относительно надежные оценки. В любой модели прогнозирования основным элементом является тренд. В большинстве рассмотренных в этой главе примеров предполагается, что тренд является линейным. Но это может быть и не так, и многие временные ряды, связанные с хозяйственной и финансовой деятельностью, выказывают нелинейный тренд. Другими элементами модели прогнозирования являются сезонные и циклические колебания, а также случайные колебания, которые невозможно предсказать в определенные временные точки. [c.215]
Большая часть примеров, приведенных в данной главе, описывают основные методы выработки моделей прогнозирования. Во-первых, в большинстве случаев предполагается, что тренд — линейный. Далее, стандартный метод выделения тренда основывается на скользящих средних, хотя мы осветили и другие методы, в том числе экспоненциального сглаживания. Во-вторых, при получении прогнозных данных использовались все имеющиеся значения, тогда как на практике это может быть не лучшим вариантом, особенно в тех случаях, когда собранные данные включают некоторые нетипичные значения. На примерах этого раздела мы рассмотрим некоторые вопросы, связанные с практическим прогнозированием, при этом предполагается, что вы уже достаточно хорошо усвоили основные методы прогнозирования, в частности знаете, как выделять тренд и выявлять и вычислять сезонные составляющие. [c.217]
Рассмотрим движение цен на акции на рис. 6.18. На графике представлено движение фондового индекса в период с 1977 по 1994 гг. Цены фиксировались и заносились на график в конце каждого квартала в течение всего указанного периода. Фондовый индекс в начале 1977 г. принят за 100. Как можно видеть, к 1994 г. фондовой индекс почти достиг отметки в 1000. Это говорит о том, что за восемнадцать лет цены на акции выросли практически в 10 раз. График показывает устойчивый рост цен на акции в период между 1977 г. и началом 1987 г. и сильный рост в последующие годы. Таким образом, общий тренд похоже соответствует кривой, которую мы рассматривали в предыдущем примере (см. рис. 6.16). Цены на акции росли очень плавно до краха в конце 80-х годов. В октябре 1987 г. цены на акции на Лондонской фондовой бирже упали в среднем на 30%. Это отражено на графике на рис. 6.18. [c.219]
Проще всего это можно проиллюстрировать на примере планирования оборота. Тот, кто осуществляет у себя этот процесс способом прибавления, например, 10% к прошлогоднему уровню для получения плана на предстоящий год, занимается прогнозированием. В принципе, прогноз - это не что иное, как продолжение тренда по обороту из прошлого в будущее. Важен тот факт, что все математические и статистические расчеты по улучшению прогнозов и повышению степени точности предсказаний еще остаются в области прогнозирования Например, речь может идти о том, чтобы выявить определенную закономерность в динамике оборота за последние годы и разработать некую модель роста. Если это удастся сделать, то при составлении прогнозов будет обеспечена большая их надежность. Однако модели предсказаний, построенные-с использованием математико-статистических методов, а также с помощью компьютера, не заменяют настоящее планирование (хотя часто такая замена очень удобна). [c.193]
Пример 6.4. По данным табл. 6.1 дать точечную и с надежностью 0,95 интервальную оценки прогноза среднего и индивидуального значений спроса на некоторый товар на момент t= 9 (девятый год). (Полагаем, что тренд линейный, а возмущения удовлетворяют требованиям классической модели (см. дальше, пример 7.8.) [c.145]
Решение. В примере 6.2 получено уравнение тренда у, = 181,32 + 25,679 (ед.). В табл. 7.1 приведен расчет сумм, необходимых для вычисления -статистики. [c.173]
Продолжим пример. Данные о динамике продажи товара за 6 месяцев из табл. 4.17 перенесены в табл. 4.18. В нее же включены данные, полученные после подстановки в уравнение тренда значений времени (t) [c.160]
| Рис. 4.1. Пример бычьего тренда на графике японской иены. | 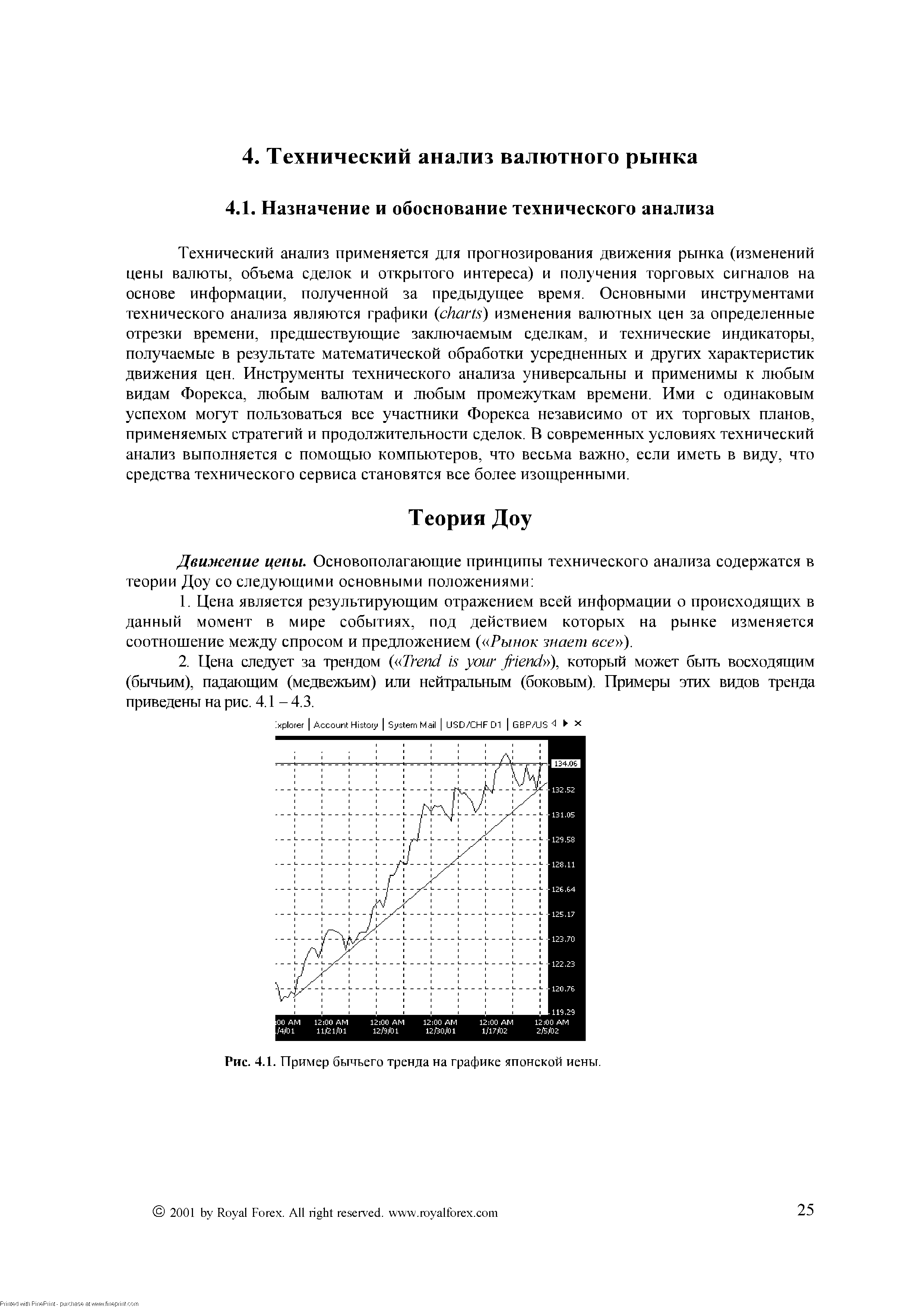 |
| Рис. 4.2. Пример медвежьего тренда и его прорыва на графике евро. | 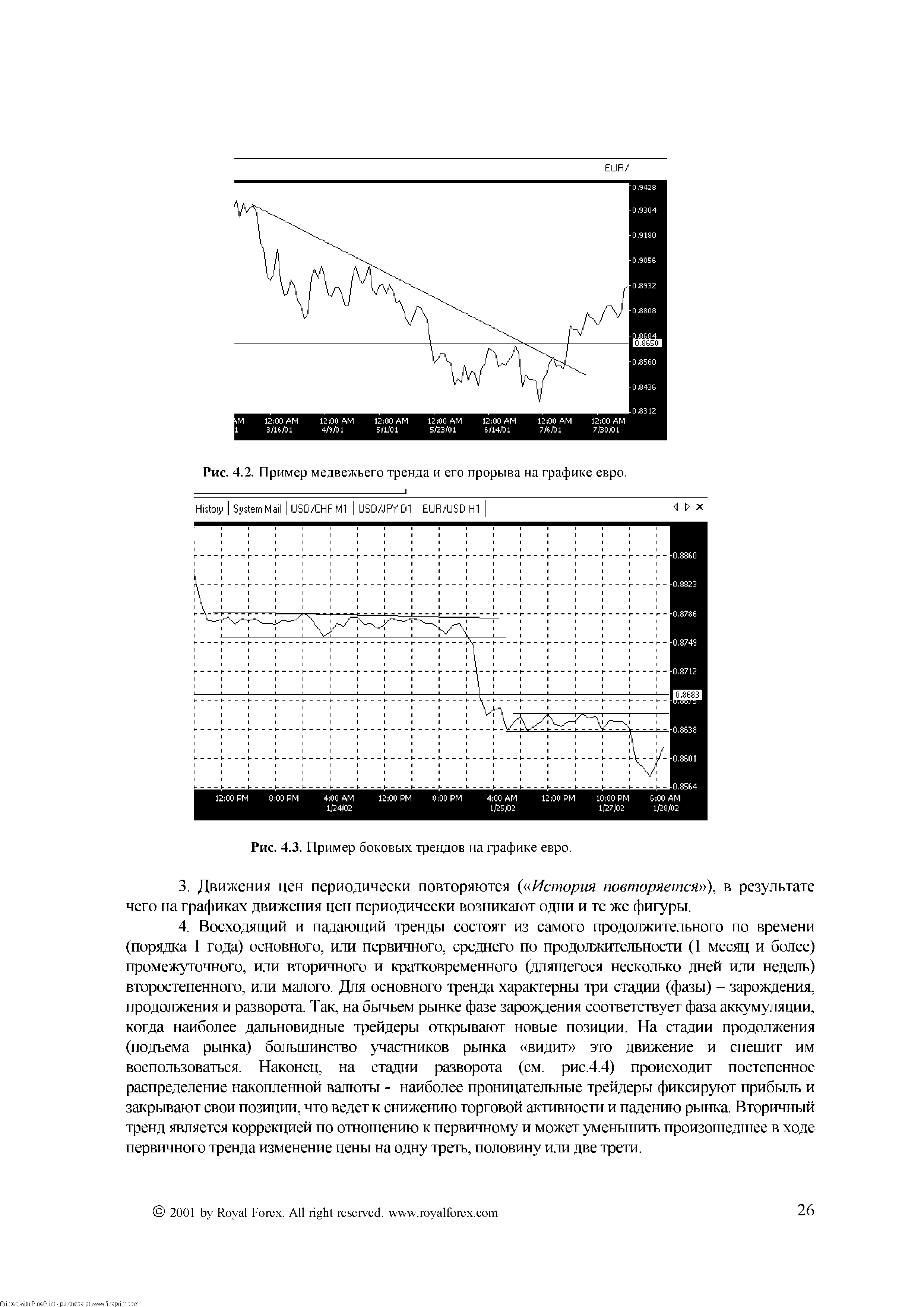 |
| Рис. 4.3. Пример боковых трендов на графике евро. | 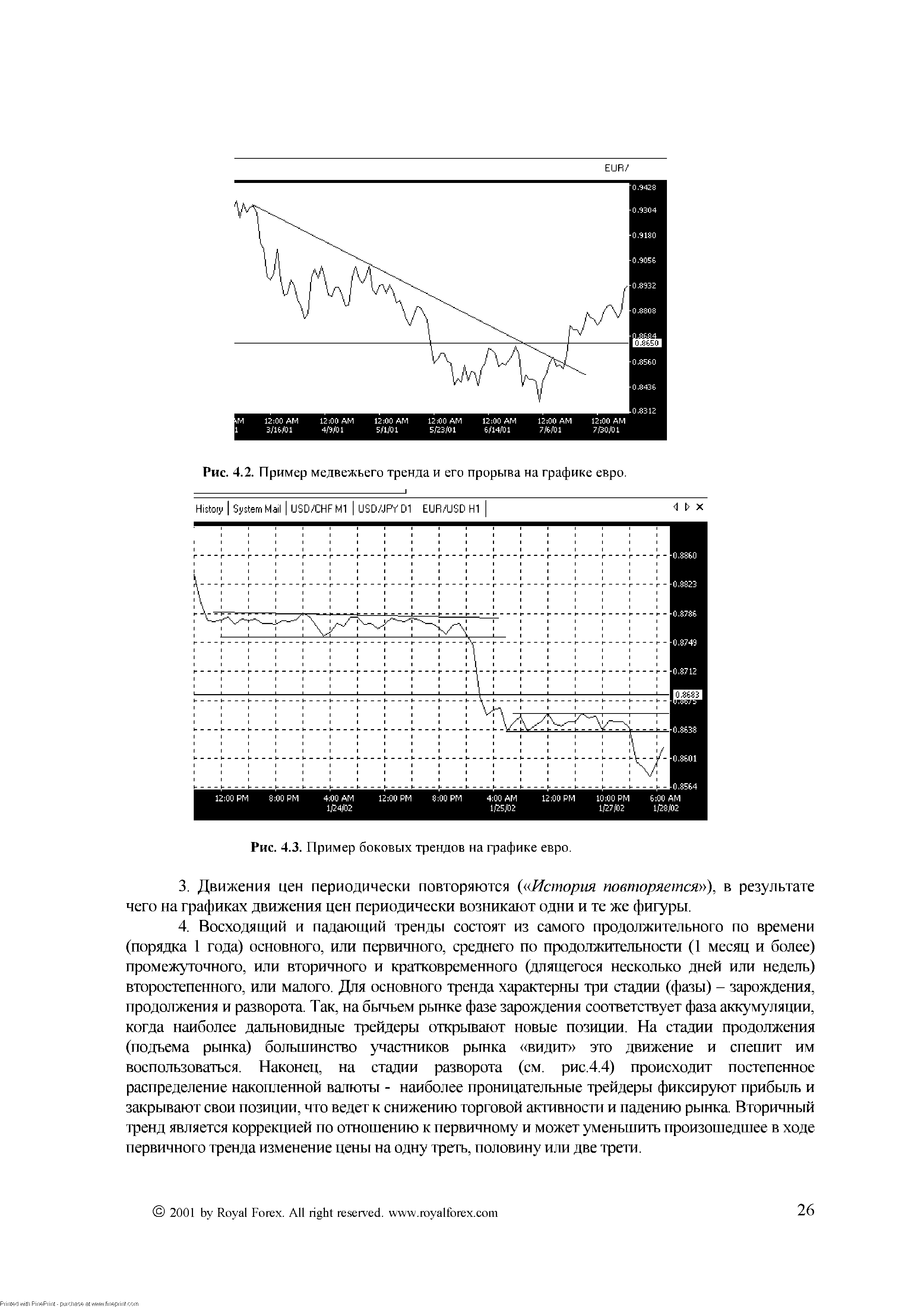 |
| Рис. 4.29. Диаграммы фигуры Медвежий флаг Пример реальных флагов на бычьем тренде показан на рис. 4.30. | 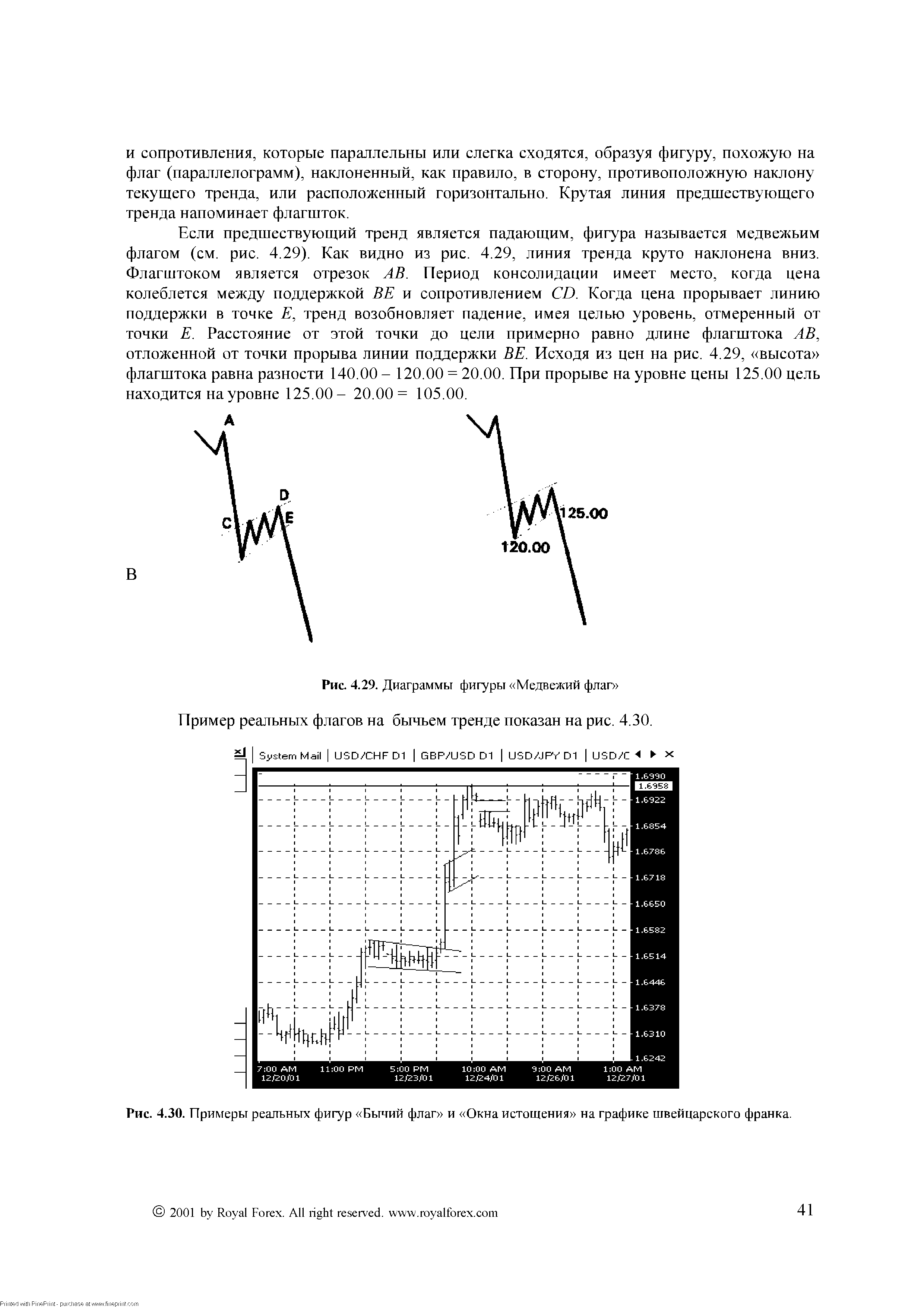 |
В данном примере для прогнозной оценки объемов продаж по сезонам 2000 г. использован метод сложения. Тренд выделен с помощью трехточечных скользящих средних, а значения 2000 г. рассчитаны уравнением регрессии. Прогнозируемые объемы продаж в каждом из периодов 2000 г. исчислены как сумма оценочных показателей тренда и средних значений сезонных колебаний в каждом сезоне (табл. 4.5). Например, среднее отклонение (колебание) за май — август 1997—1999 гг. определяется так (9,33 + + 11,67 + 12,33 3= 11,И) и т.д. [c.80]
Пример. Дадим прогноз валового национального продукта США на 1979—1980 гг. в текущих ценах по данным4 за предшествующие 50 лет. Используем систему STADIA 5.O. Используя блок статистики системы и процедуру Простая регрессия (тренд) , получим оценки полиномиальной модели. Точность модели повышалась, пока степень полинома не достигла пятой [c.102]
Первым этапом построения тренда является выбор типа аналитической функции. В нашем примере основанием для применения линейного уравнения в качестве трендовой модели является существующая тенденция снижения уровня процентных ставок без наличия каких-либо осциллятивных колебаний. [c.612]
На рис. 9.1 достаточно хорошо видно, что тренд урожайности выражен прямой линией. Исходный ряд уровней короткий, поэтому на данном примере нельзя использовать другие приемы. Применим их к анализу динамики индекса цен на нетопливные товары развивающихся стран за 1979 - 1995 гг.1 [c.326]
Для выявления типа колебаний воспользуемся приемом, предложенным М. Кендалом. Он состоит в подсчете так называемых поворотных точек в ряду отклонений от тренда м,, т. е. локальных экстремумов. Отклонение, либо большее по алгебраической величине, либо меньшее двух соседних, отмечается точкой. Обратимся к рис. 9.2. При маятниковой колеблемости все отклонения, кроме двух крайних, будут поворотными , следовательно, их число составит п - 2. При долгопериодических циклах на цикл приходятся один минимум и один максимум, а общее число точек составит 2(и /), где / - длительность цикла. При случайно распределенной во времени колеблемости, как доказал М. Кендэл, число поворотных точек в среднем составит 2/3 (п - 2). В нашем примере при маятниковой колеблемости было бы 15 точек, при связанной с 11-летним циклом было бы 2-(17 11) 3 точки, при случайно [c.343]
Рассмотрим методику прогнозирования по тренду с учетом колеблемости на примере цен на нетопливные товары развивающихся стран, тренд и колеблемость которых была измерена в параграфах 9.6 и 9.7 (табл. 9.4 и 9.7). За основу прогнозов возьмем параметры, полученные методом многократного скользящего выравнивания. Параллельно будет показана и методика расчетов при однократном выравнивании. [c.358]
Из этой вступительной части вы должны уяснить, что увеличение числа точек при вычислении скользящих средних ведет к большему сглаживанию линии тренда. Поэтому можно утверждать, что чем больше точек взято для вычисления скользящих средних, тем линия тренда лучше . Но при этом может возникнуть вопрос а почему не рассчитать средние по 10, 11 или даже 15 точкам Дело в том, что чем больше точек мы берем для вычисления скользящих средних, тем меньше конечных значений мы получаем. Так, сравним два набора скользящих средних, рассчитанных в нашем примере. Мы получили 13 трехточечных скользящих средних и только девять семиточечных скользящих средних. [c.191]
Как и в предыдущем примере, когда мы применяли метод сложения, тренд можно определить графически по средним скользящим. На графике (рис. 6.12) показаны данные по стоимости аренды, а также трехточечные скользящие средние. Линия тренда проведена через скользящие средние и продолжена дальше, с тем чтобы получить прогнозные показатели по каждому периоду 1998 г. Согласно графику, эти показатели на 1998 г. таковы [c.207]
Наиболее распространенным примером выявления наличия автокорреляции в отклонениях от тренда или от регрессионной модели является использование критерия Дарбина—Уотсона (d), который рассчитывается по формуле [c.86]
Цена следует за трендом ( Trend is your friend ), который может быть восходящим (бычьим), падающим (медвежьим) или нейтральным (боковым). Примеры этих видов тренда приведены на рис. 4.1 - 4.3. [c.25]
Линия тренда. Линия тренда является главным исходным элементом при анализе графика цены. Поскольку рынок в любом направлении движется не по прямой линии, а зигзагами, взаимное расположение верхних и нижних точек этих зигзагов позволяет, используя технические инструменты компьютерной программы, провести линию, соединяющую самые нижние или самые верхние точки зигзагов графика цены (см. рис. 4.1-4.3). Чтобы провести линию тренда, достаточно иметь две точки, через которые она проводится, и еще одну точку для подтверждения тренда. На графике бычьего тренда линии тренда проводят черех точки, выступающие вниз, а на графике медвежьего - вверх. Линия тренда и примерно параллельная ей линия, проведенная через наиболее выступающие по отношению к другим точки противоположной стороны графика, образуют торговый канал и являются границами этого канала. Примеры торговых каналов приведены на рис. 4.9,4.10. [c.30]
Смотреть страницы где упоминается термин Примеры трендов
: [c.40] [c.197] [c.199] [c.219]Смотреть главы в:
Внутридневная торговая система 5 баллов за успех -> Примеры трендов
