Как скажется нелинейность функции полезности на изложенном в этой главе анализе двухуровневой системы хранения запасов [c.167]
В заключение настоящего раздела сделаем следующее замечание. Основные технические трудности анализа механизмов страхования возникают из-за нелинейности функции полезности страхователя. В то же время, именно эта нелинейность, отражающая его несклонность к риску, делает страхование возможным и взаимовыгодным для страхователя и страховщика. Поэтому для упрощения моделей рассмотрим возможные способы учета несклонности страхователя к риску, не использующие в явном виде функции полезности. Для этого введем в его целевую функцию рисковую премию, отражающую ценность страхового возмещения, получаемого при наступлении страхового случая. [c.49]
Стоимость информации трудно оценить, так как во многих случаях она выражается существенно нелинейной функцией и иногда одна и та же информация имеет значение одновременно для нескольких проектов, находящихся на рассмотрении фирмы. Более того, наличие некоторых видов информации может иногда побудить фирму искать именно такие проекты, для которых эта информация оказалась бы полезной. [c.126]
Как изменились бы рассуждения настоящей главы, если бы функция полезности была нелинейной [c.143]
В приведенной постановке задача потребительского выбора является задачей нелинейного программирования - см. главу 8, раздел 3. Однако если на каком-то потребительском наборе (x,,Xj) бюджетное ограничение р +р < I будет выполняться в виде строгого неравенства, то мы можем увеличить потребление какого-либо из продуктов и тем самым увеличить функцию полезности. Следовательно, набор (х,0 0), максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е. рр +рр =1. Графически это означает, что решение (xt°,x2°) задачи потребительского выбора должно лежать на бюджетной прямой (см. рис. 9.3), которую удобнее всего провести через точки пересечения с осями [c.141]
В более сложных случаях (например, при нелинейной зависимости функции полезности от потребления прочих товаров) спрос на табачные изделия при 0< <1 будет также зависеть от доходов потребителей. [c.158]
Оптимизация портфелей, содержащих нелинейные инструменты, чаще его осуществляется с использованием функций полезности. [c.715]
После определения характеристик следует выбрать подходящие уровни. Их число определяет число оцениваемых параметров, а также влияет на число объектов, которые будут оцениваться респондентами. Чтобы облегчить задачу, стоящую перед респондентами, и при этом оценивать параметры с достаточной точностью, желательно ограничить число уровней. Функции полезности или частной ценности для уровней характеристики могут оказаться нелинейными. Например, потребитель предпочитает средний по размеру автомобиль маленькому или большому автомобилю, Аналогично и функция полезности для цены может носить нелинейный характер. Потеря полезности при переходе от дешево го автомобиля к автомобилю средней цены может быть намного меньше, чем потеря полезности при переходе от автомобиля средней цены к дорогому. В этих случаях используют, по крайней мере, три уровня. Для некоторых характеристик естественно наличие двух уровней — может иметь или не иметь люк в крыше, [c.794]
Эта функция полезности является линейной относительно у и нелинейной относительно х. [c.33]
Если функция полезности является линейной относительно х и нелинейной относительно у, то можно в общем виде представить ее следующим образом [c.33]
| Рис. 2.11. Функция полезности нелинейна относительно х | 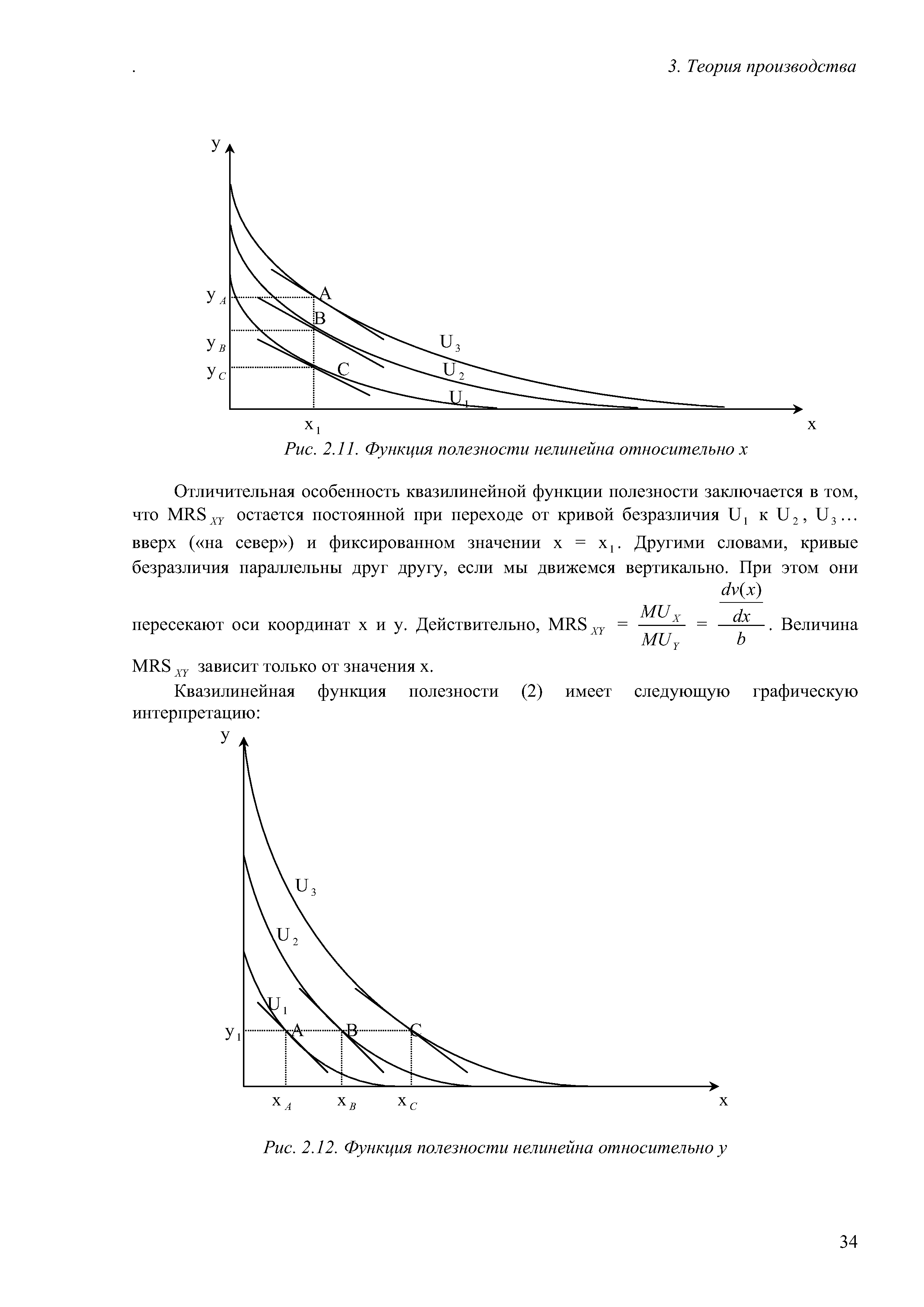 |
| Рис. 2.12. Функция полезности нелинейна относительно у | 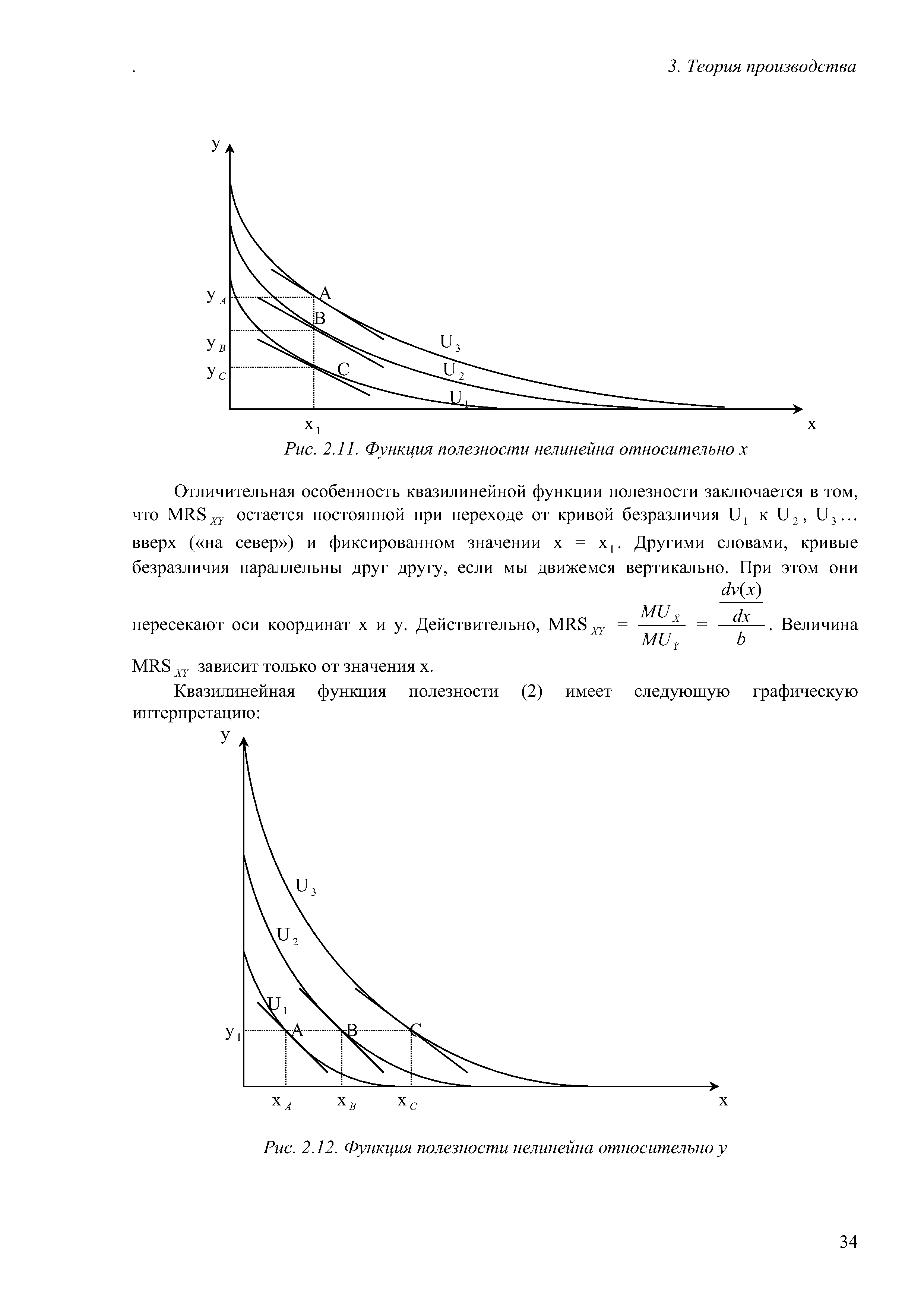 |
Графическое изображение соотношения между экономией от повышения качества дизельного топлива и сопутствующими ему затратами приведено на рис. 4.1 в форме т.н. коробки качества - совмещенном графике, по ординате которого показаны одновременно дополнительные расходы по сероочистке и получаемая от этого экономия, а по абсциссе - содержание серы. Рис. 4.1 и табл. 4.1 подтверждают основные из упомянутых ранее закономерностей. Это -нелинейность зависимости экономии и затрат от значений качественных параметров, наличие предела насыщения, снижающаяся предельная полезность качества, повышающиеся предельные затраты на дополнительный прирост качества. Отсюда вывод не существует постоянных коэффициентов значимости качественных характеристик продукции. Они являются функциями оцениваемых свойств. Поэтому, строго говоря, все способы синтеза комплексного показателя качества продукции, основанные на применении фиксированных коэффициентов значимости единичных показателей по формулам (3.14), (3.15), (3.16) искажают действительность. Избежать этого можно, применяя прямой, экономически прозрачный показатель полезности продукта. В самом способе его расчета и в структуре его компонентов заключена возможность учета нелинейности и всех других особенностей реального соотношения эффекта повышения качества и затрат по его обеспечению. Полностью отвечает сложной природе качества такой расчет его уровня, при котором непосредственно соизмеряются полезность продукции и затраты на её изготовление и эксплуатацию. Такой показатель называется интегральным. [c.86]
РИС. 3.3 представляет собой схематическое изображение соотношения между доходностью и ценой облигации. Кривая, известная как кривая цены-доходности облигации, нелинейна и имеет отрицательный наклон. Моделирование изменения цены в результате изменения доходности облигации может оказаться очень сложным. Тем не менее, исходя из нашего понимания разложения рядов Тейлора, мы должны быть способны приблизиться к функции "цена-доходность" на определенном этапе разложения рядов Тейлора. Можно, например, применить первую производную цены облигации по доходности, вторую, третью и т.д. Фактически мы увидим далее, что применение рядов Тейлора всего лишь первых двух порядков прекрасно позволяет оценить изменение в цене облигации при малом изменении доходности. Более того, если мы разделим разные элементы рядов Тейлора на цену облигации, то получим очень полезный результат, показывающий волатильность цены облигации. [c.139]
Решение этой системы и будет являться начальным приближением параметров. Очевидно, для того чтобы данный метод работал , необходимо, чтобы эта система нелинейных уравнений решалась довольно легко, например аналитически. 9.6.4. Разложение в ряд Тейлора по независимым переменным. Основой итеративной минимизации суммы квадратов является разложение функции регрессии в ряд Тейлора до линейных членов по параметрам. Для нахождения грубого начального приближения иногда бывает полезна процедура аппроксимации регрессии путем разложения ее в ряд Тейлора по независимым переменным Хг. Будем для простоты считать [c.315]
В общем случае функция Ц(х) — нелинейна, так как, во-первых, возможно замещение продуктов, во-вторых, полезность измеряется, как правило, в порядковой шкале. Будем для простоты предполагать вогнутость функции U(x) и существование оптимального решения задачи планирования. [c.60]
Лично я нахожу работы Вентуорта в этой области весьма интересными. В них содержится ряд довольно любопытных положений. В первую очередь они напрямую атакуют классическую теорию полезности, что автоматически ожесточает против них всех профессионалов из исследовательских подразделений в области методов управления. Нелинейность функции полезности капитала, лежащая в основе классической теории, для этих людей священна. Вентуорт же проводит параллель между максимизацией моды и эволюцией. На этом он основывает свою гипотезу выживания. Краткий сравнительный обзор этих двух подходов выглядит следующим образом [c.118]
Теперь обратимся к случаю нелинейной зависимости функции полезности F от качественного параметра Kf. ПриК ,= 1 F0=l+0,5 l°-5=l,5. [c.50]
Представления (6) и (7) показывают, что AI и Ап (две нелинейных функции от А) можно представить как огибающую линейных функций от А. Эта техника называется квазилинеаризацией правые части (6) и (7) суть квазилинейные представления AI и Ап. Мы еще будем встречаться с некоторыми полезными применениями этой техники в следующих параграфах. [c.261]
Идея анализа в модели Харбергера состоит в том, чтобы проводить исследование в системе общего равновесия на основе малых приращений. В этих условиях нелинейные соотношения могут быть линеаризованы, и конечный результат состоит в решении системы линейных уравнений, где влияние изменений в налоговой системе на цены, объемы потребления факторов производства и полезность потребителя может быть выражено через эластичности функции полезности и производственных функций. [c.75]
