Дополнительные настройки оптимизации выполняются в диалоговом окне Параметр поиска решения. В частности, можно ограничить время выполнения поиска решения и выполнения промежуточных вычислений, максимальное время — не более 9 часов, точность, с которой найденное решение соответствует целевому значению, допустимое отклонение для переменных от оптимального значения. Для задач с нелинейной целевой функцией задается параметр сходимости, который влияет на прекращение поиска. Если относительные изменения значения целевой функции за последние пять итераций меньше указанного числа, поиск прекращается. Выполняется установка типа модели — линейная, если целевая функция линейная. Можно выводить результаты итераций, выполнять автоматическое масштабирование параметров модели. [c.457]
При решении задачи можно выбрать метод экстраполяции оценок переменных для каждого шага поиска — линейная или квадратичная (для задач с нелинейной целевой функцией), метод численного дифференцирования для целевой функции — прямые или центральные разности (для задач с нелинейной целевой функцией), метод поиска — метод Ньютона (требуется много оперативной памяти) или метод сопряженных градиентов (больше итераций). Основным ограничением модели является максимальное число переменных — 200. Несколько оптимизационных моделей на одном листе можно сохранять и загружать по мере необходимости. [c.457]
Среди параметров имеются дискретные (в том числе целочисленные )-диаметр, количество насосов и перекачивающих станций, намывных машин и их секций, а среди ограничений - линейные и нелинейные. Целевая функция является разрывной. [c.65]
Нелинейность выходной функции активации /( ) принципиальна. Если бы нейроны были [c.43]
Соболев А.И. (1978). Нелинейные аналоги функции Шеп- [c.312]
Для определения корреляционной связи в нелинейных моделях используют множественное корреляционное отношение, при этом для вычисления остаточной дисперсии используется нелинейная форма функции отклика у. [c.120]
Основное назначение машины — исследование различных систем методом электрического моделирования (в частности, исследования в натуральном масштабе времени совместно с реальными приборами автоматического регулирования). На ней можно решать дифференциальные уравнения, содержащие до шести нелинейных зависимостей функции от одной переменной или перемножения двух переменных (при любом сочетании этих зависимостей по количеству в пределах шеста). [c.125]
К моделям нелинейного программирования относятся задачи с нелинейной целевой функцией и линейными ограничениями [c.247]
Экстремальные задачи, в которых либо ограничения, либо целевая функция, либо и то и другое нелинейны, называются задачами нелинейного программирования (в нашей задаче нелинейна целевая функция). К сожалению, пока не имеется общих методов, подобных методу последовательного улучшения плана или симплекс-методу в линейном программирования, которые позволяли бы решать любые задачи нелинейного программирования. Поэтому здесь будут указаны возможности решения лишь для некоторых, впрочем, весьма важных частных случаев. [c.97]
В том случае, когда нелинейна целевая функция, возникают другие затруднения. В первой главе было указано, что решение задачи линейного программирования обязательно находится в некоторых (возможно, в нескольких) крайних точках множества допустимых планов. Но при нелинейной целевой функции экстремум может достигаться не только на границе, но и внутри допустимой области (рис. 9). [c.98]
Линейное и нелинейное — отличаются функциями. Динамическое программирование служит для выбора наилучшего плана выполнения многоэтапных действий, когда результат каждого последующего этапа зависит от предыдущего. [c.262]
В более сложных случаях (например, при нелинейной зависимости функции полезности от потребления прочих товаров) спрос на табачные изделия при 0< <1 будет также зависеть от доходов потребителей. [c.158]
Сбережения в коротком периоде тоже являются нелинейной возрастающей функцией от дохода. При низком уровне дохода предельная склонность к сбережению относительно велика, так как существует стремление людей за счет сбережений перейти на более высокий уровень благосостояния. И когда уровень благосостояния стабилизируется, люди снижают долю сберегаемого дохода. [c.55]
В зависимости от этого выбора устанавливается способ расчета затрат на хранение и штрафы. При минимизации расходов за период эти затраты чаще всего исчисляются по ожидаемому остатку (дефициту) к концу периода. В противном случае предпочтителен расчет по импульсу этих величин — произведению средней недостачи (запаса) на время ее (его) существования. Этот же подход применяется в моделях с повышенной ролью фактора времени, где необходимо учитывать время простоя потребителей. Иногда величина штрафа не зависит не только от момента появления недостачи, но и от ее величины, так что некоторая постоянная сумма выплачивается при первом же необслуженном требовании. В этом случае штраф определяется вероятностью недостачи. Как правило, затраты на хранение или штрафы являются линейной функцией упомянутых величин. Применительно к особо ответственным системам (объекты энергетики, жизнеобеспечения, системы военного назначения) строятся специфические (обычно нелинейные) штрафные функции. [c.43]
Если целевая функция является некоторой функцией найденных значений переменных, то для решения задачи применяют методы нелинейного программирования, в частности, его простейшую форму — квадратичное программирование. [c.153]
Таким образом, целевая функция (2.9) вместе с ограничениями (2.11), (2.17) и (2.18) представляет собой экономико-математическую модель задачи необходимо найти такие значения темпов выполнения работ сетевой операционной модели (количества добавляемых на процессы технологических звеньев), которые обеспечивают строительство объекта в плановые сроки при минимуме затрат на передислокацию строительно-монтажных подразделений. Данная задача относится к классу нелинейных задач целочисленного программирования. Даже в упрощенном варианте организации строительства без учета сменности работ решение задачи представляет определенную трудность. [c.50]
Зависимость отдельных составляющих целевой функции от числа пунктов разгрузки, включенных в какой-либо вариант внешнего транспортного обеспечения и условно рассматриваемых как непрерывные функции в области целочисленных величин числа пунктов разгрузки пгв, представлена на рис. 27. Как видно из рисунка, с увеличением числа пунктов разгрузки возрастают суммарные затраты на их организацию и уменьшаются транспортные расходы по доставке труб к месту работ. Следовательно, целевая функция как сумма указанных составляющих имеет экстремум при некотором значении числа пунктов разгрузки. Учитывая нелинейную зависимость функционала и его отдельных составляющих от числа вводимых пунктов разгрузки и искомых переменных, для решения поставленной задачи не могут быть применены классические методы математического программирования (например,. линейного). Как известно из курса высшей математики, математическое программирование — область математики, разрабатывающая теорию и методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных. Само название программирование взято из линейного программирования, где оно обычно обозначает распределение наилучшим образом ограниченных ресурсов для достижения поставленных целей. Следовательно, термин программирование здесь можно заменить термином планирование . [c.145]
Налицо, хотя и небольшая, но явная погрешность расчета по формуле (3.21). При более сложных формах нелинейных функций полезности она может совершенно исказить действительную величину комплексного показателя. Избежать этого можно введением фактора нелинейности в формулу (3.21) в виде показателя степени ai при (К,-1)- Тогда [c.50]
Графическое изображение соотношения между экономией от повышения качества дизельного топлива и сопутствующими ему затратами приведено на рис. 4.1 в форме т.н. коробки качества - совмещенном графике, по ординате которого показаны одновременно дополнительные расходы по сероочистке и получаемая от этого экономия, а по абсциссе - содержание серы. Рис. 4.1 и табл. 4.1 подтверждают основные из упомянутых ранее закономерностей. Это -нелинейность зависимости экономии и затрат от значений качественных параметров, наличие предела насыщения, снижающаяся предельная полезность качества, повышающиеся предельные затраты на дополнительный прирост качества. Отсюда вывод не существует постоянных коэффициентов значимости качественных характеристик продукции. Они являются функциями оцениваемых свойств. Поэтому, строго говоря, все способы синтеза комплексного показателя качества продукции, основанные на применении фиксированных коэффициентов значимости единичных показателей по формулам (3.14), (3.15), (3.16) искажают действительность. Избежать этого можно, применяя прямой, экономически прозрачный показатель полезности продукта. В самом способе его расчета и в структуре его компонентов заключена возможность учета нелинейности и всех других особенностей реального соотношения эффекта повышения качества и затрат по его обеспечению. Полностью отвечает сложной природе качества такой расчет его уровня, при котором непосредственно соизмеряются полезность продукции и затраты на её изготовление и эксплуатацию. Такой показатель называется интегральным. [c.86]
Нелинейное программирование - обобщение случая линейного программирования, когда критерий — нелинейная функция решений с нелинейными ограничениями. Общих методов решения здесь не существует. Более или менее приемлемые способы решения имеются для случая, когда функция критерия К и ограничения — вогнутые функции и когда К — квадратичная функция решений, а ограничения линейны (квадратичное программирование). [c.308]
Графики на рис. 2.3(Ь) и 2.3(с) показывают криволинейную функцию затрат, подразумевающую, что изменение суммы удельных переменных затрат непрерывно изменяется по мере увеличения/уменьшения объема деятельности. На рис. 2.3(Ь) наклон кривой совокупных затрат уменьшается по мере роста объема деятельности, указывая на то, что удельные переменные затраты снижаются, а непрерывно возрастающий наклон кривой на рис. 2.3(с) указывает на увеличение удельных переменных затрат. Вам следует отметить, что и на рис. 2.3(Ь), и на рис. 2.3(с) темпы увеличения/уменьшения удельных переменных затрат непостоянны. В следующей главе мы будем обсуждать одну из возможных причин нелинейного поведения затрат. [c.76]
Переменные. Лицензионные платежи и компьютерные дискеты — чем больше объем выпуска, тем выше их общая величина. Поскольку лицензионные платежи имеют фиксированную ставку платежа за каждый заказ, функция затрат будет линейной. Исходя из того, что различные заказы могут потребовать разное количество дискет, функция затрат будет нелинейной, поскольку [c.78]
Линейное программирование позволяет глубоко проанализировать задачу, и все же оно предполагает те же пять допущений, о которых говорилось выше при обсуждении метода анализа вклада в расчете на единицу ограничивающего фактора, а именно наличие определенности линейность функции затрат линейность функции выручки равенство объема реализации объему выпуска и независимость продуктов. Кроме того, мы предположили, что продукты делимы, т.е. можно произвести и продать нецелое их количество, что не всегда соответствует действительности. (Это предположение в неявной форме было присуще и методике анализа вклада/релевантных затрат на единицу ограничивающего фактора.) Данные недостатки преодолеваются в более совершенных методах анализа, например, в нелинейном или целочисленном программировании. Но даже и такие методы не полностью гарантируют точность результатов, а их чрезмерная сложность может помешать их пониманию и эффективному использованию. [c.376]
Если ввести новые переменные vh = q>h(x), то для нахождения параметров понадобится решать ту же самую задачу, что и для (5.2). В некоторых случаях к виду (5.2) удается свести функции, нелинейные относительно параметров. Например, степенная производственная функция (3.1) сводится логарифмированием к линейной относительно параметров [c.111]
Теперь обратимся к случаю нелинейной зависимости функции полезности F от качественного параметра Kf. ПриК ,= 1 F0=l+0,5 l°-5=l,5. [c.50]
Форма зависимости в соответствии с характером изменения результативного признака может быть линейной или нелинейной. Нелинейная функция может быть линеаризована (приведена к линейному виду с помощью логарифмирования). Чаще других в маркетинге используются следующие уравнения регрессии (табл. 5.6). [c.202]
| Рисунок 12. Выявление нелинейной составляющей функции у = 1 Ох + зш(л") + 0.5// после вычитания линейной зависимости у = 1 O.Y . ( Здесь г) - гауссовый случайный шум) | 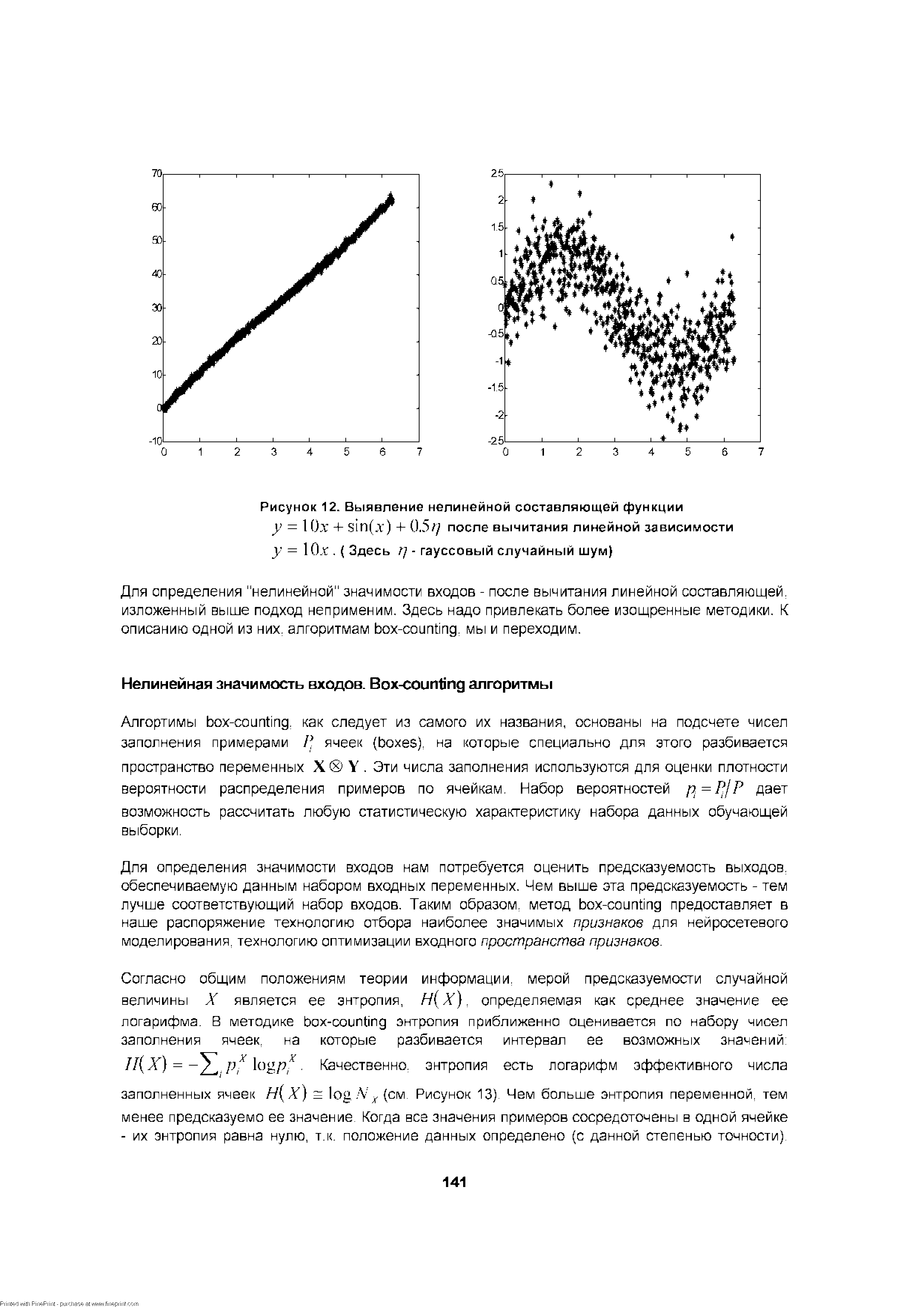 |
Отметим, что впервые в экономике работы по построению и использованию производственных функций были осуществлены в США для анализа состояния сельскохозяйственного производства. В 1909 г. Митчерлих предложил нелинейную производственную функцию удобрения — урожайность. Независимо от него Спиллман предложил показательное уравнение урожайности. В 1928 г. Ч. Кобб и П. Дуглас на основе данных по обрабатывающей промышленности США за период 1899—1922 гг. (т. е. по несельскохозяйственным отраслям) представили функцию [c.138]
Соболев А.И. (1978). Нелинейные аналоги функции Шепли / В кн. Теоретико-игровые вопросы принятия решений. 9-18. Л. Наука. [c.237]
Наблюдавшиеся в период с 1992 по март 1995 г. изменения рынка были средними по масштабу. Компоненты цены были масштабированы относительно слабо для того, чтобы можно было получить средние цены за весь период. Другая причина использования слабого масштабирования цен заключается в стремлении найти цену для нового объекта с учетом других компонент. Наблюдения были разделены на временные окна для 1992, 1993 и 1994 гг. Анализ чувствительности выявляет изменение цен на двухкомнатные квартиры в центре Хельсинки (табл. 8.1). Нелинейность формы функции прослеживается достаточно ясно. [c.181]
Лх . Для нелинейных функций (как в нашем случае) и значительных Дх] правильнее будет брать средние значения частных производных и вычислять AKUXj по формуле [c.71]
Для района в целом также имеет место выпуклость функции "затраты — выпуск". Но она обусловлена также и необходимостью перехода на экономически менее эффективные объекты разработки в целях получения дополнительной добычи. И для отрасли в целом эта функция выпукла вниз, что обусловлено еще одним фактором — фактором географической отдаленности. Для получения новых мощностей по добыче отрасль вынуждена переносить фронт работ во все более отдаленные и необустроенные районы. Здесь уже имеет место нелинейность экстенсификации. Таким юбразом, на всех трех уровнях прослеживается рост удельных ных вложений в новые мощности с увеличением [c.68]
На рисунке 10.1 показана взаимосвязь между чистой приведенной стоимостью (NPV) и внутренней нормы прибыли (IRR) — чем больше ставка дисконтирования, тем меньше NPV. Обратите внимание, что указанная зависимость нелинейна. Точка, в которой график NPVпересекает ось абсцисс, дает внутреннюю норму прибыли это и есть ставка дисконтирования, при которой NPV равна нулю. Подобный график можно было бы использовать для определения IRR, но чертить его вручную — занятие утомительное, так как для достаточно точного построения функции потребовалось бы рассчитать несколько значений NPV при разных ставках дисконтирования. [c.455]
