| Рис. 67. Графики спуска бурильной колонны при использовании различных критериев оптимальности процесса (для условий СКВ. 189) | 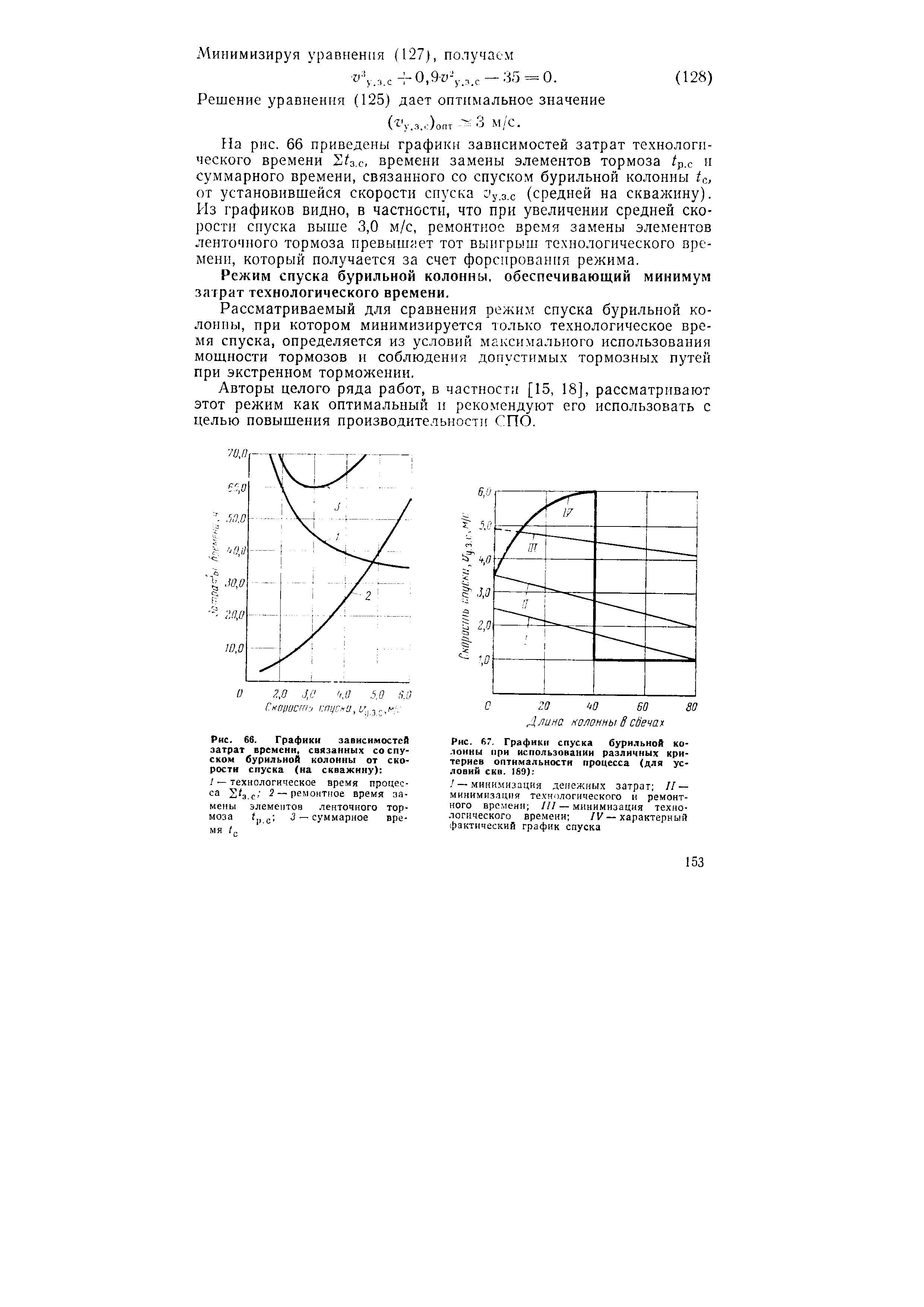 |
Для обеспечения оптимального процесса разработки нефтяного месторождения в результате экономического анализа должно быть установлено рациональное распределение капитальных вложений на бурение эксплуатационных скважин и создание объектов внутри-контурного заводнения. [c.71]
Особым видом относительных статистических показателей являются отношения фактически наблюдаемых величин признака к его нормативным, плановым, оптимальным или максимально возможным величинам. Это широко распространенные на производстве показатели выполнения норм выработки, норм расхода материалов и других ресурсов. Отношения наблюдаемых величин признака к оптимальным или плановым характеризуют приближение изучаемого процесса к идеалу. Так, если оптимальная норма потребления мяса взрослым мужчиной на Северо-Западе России составляет 80 кг в год, а фактическое среднедушевое потребление составило в 1992 г. 58 кг, то ясно, что размер и структура потребления далеки от оптимальной всего 72%. Всякое превышение или недобор до оптимальной величины, всякое отклонение от 100% такого относительного показателя (в любую сторону) означают нарушение оптимальности процесса, даже перевыполнение плана, если план не лозунг, а научно обоснованная, взаимосвязанная система объемов производства отдельных видов продукции. В этом случае превышение планового выпуска одного вида продукции, например выплавки стали без согласованного изменения производства станков, прокатных станов, других средств обработки металла, есть попросту омертвление затрат и бесполезный перерасход природных ресурсов, труда. [c.49]
Однако САПР как систему автоматизированного проектирования отличают от других разновидностей АС ряд особенностей, обусловленных ее назначением. Подход к созданию САПР должен основываться на том, что в ней реализуется установившийся оптимальный процесс генерирования технических документов, обеспечивающий непрерывное воплощение новых идей и выполнение новых заказов. [c.29]
Математическая теория оптимальных процессов / Л. С. Понтрягин, [c.221]
Е. В. Математическая теория оптимальных процессов. - М. Наука. - [c.30]
Для построения оптимального процесса изменений важно учитывать индивидуальные способы принятия изменений (типичные для каждого механизма). Можно выделить следующие индивидуальные механизмы принятия изменений [c.183]
Часто высказывается мнение, что хороший разработчик должен уметь проектировать оптимальный процесс с нуля и что исследование существующей практики идет во вред оптимальной организации. Это, возможно, и правда, но хороших разработчиков не так много, а улучшение существующих методов работы может хотя и не вести к идеальной организации, но обходится дешевле, чем новая разработка. Подробный учет практики работы позволяет по крайней мере удостовериться, что предлагаемые нововведения вообще возможны. При этом ведется пристальное наблюдение за суще- [c.121]
Принцип двойственности как ключ к решению широкого класса экстремальных задач распространяется также на ряд других областей математического программирования, на математическую теорию оптимальных процессов, [c.71]
В математической теории оптимальных процессов — совокупность управляющих параметров, переводящих систему из одного фазового состояния в другое. [c.369]
Математическая теория оптимальных процессов 185 [c.472]
Ф методы математической кибернетики математическая теория оптимальных процессов. Объекты при проведении экономического анализа предприятия могут быть внутренними и внешними. Внутренние Ф администрация <> экономические службы предприятия [c.311]
Основные задачи выявления предельных возможностей макро-управляемых систем и расчета соответствующих оптимальных процессов таковы. [c.12]
Сделаем допущение, что в оптимальном процессе (p(u, и ф 0 это позволяет провести замену переменной [c.55]
Тот факт, что оптимальный процесс теплового контакта с источником постоянной температуры может иметь больше чем один изотермический участок, обнаружен В.Н.Орловым [157] для весьма экзотического закона теплопереноса [c.76]
Найдем связь между продолжительностью процесса т, приращением энтропии системы D и приращением энтропии источника ASo. На оптимальном процессе скорости изменения D и ASo постоянны, так что [c.78]
Следствие. Когда на состав и энтропию рабочих тел при t — г ограничений не наложено (т — 0), энтропия системы в оптимальном процессе при любых законах тепло- и массопереноса растет с постоянной скоростью, а каждое из рабочих тел на протяжении всего процесса контактирует только с одним из резервуаров. [c.96]
Тепломеханические системы. Для тепломеханических систем, где интенсивной переменной является температура, а экстенсивными — объем, энтропия и внутренняя энергия, из сформулированной в предыдущем разделе теоремы следует, что оптимальные процессы в [c.96]
Во многих практически важных случаях структура оптимального решения не зависит от кинетических характеристик процессов, а энтропия системы в оптимальном процессе растет с постоянной либо кусочно постоянной скоростью. Задача о максимальной мощности имеет ту же структуру оптимального решения, что и задача о максимальной работе, так как отличается от последней лишь тем, что продолжительность г не фиксирована, а выбирается из условия максимума отношения А (т)/(т). [c.109]
Предельным возможностям тепловых машин посвящено огромное число работ (см. обзоры [48, 60]). В этой главе мы рассмотрим общие свойства оптимальных процессов в таких системах и характерные постановки задач. При этом выделим два типа машин. В первом случае рабочее тело предполагается однородным и значения его интенсивных переменных меняются только во времени. Рабочее тело может поочередно вступать в контакт или прерывать контакт с другими элементами системы. Такую машину называют машиной с сосредоточенными параметрами. [c.134]
Таким образом, АДЦ представляет собой сложную систему тепло-и массообменных аппаратов. Естественный способ ее оптимизации заключается в разбиении системы на отдельные аппараты и оптимизации на первой стадии процесса в каждом из них в функции параметров, от которых зависит режим других аппаратов. На второй стадии эти параметры подбирают так, чтобы необратимость процесса в целом оказалась минимальной. При этом на первом этапе используют условия оптимальности процессов необратимого тепло- и массопереноса, полученные в этой и предыдущей главах. В качестве примера такого подхода рассмотрим АДЦ с источниками конечной емкости. [c.210]
Будем предполагать, что скорости движения фаз постоянны и соответствуют режиму идеального вытеснения, а поток массопереноса пропорционален разности химических потенциалов. В этом случае, как показано выше (см. гл. 2), в оптимальном процессе изотермического массопереноса отношение концентрации перераспределяемого компонента в источнике уп(1) к равновесной концентрации у (х(1)) должно быть постоянным в любом сечении. Здесь х — концентрации перераспределяемого компонента в растворе. Если k — коэффициент мае- [c.210]
Из сравнения этих равенств следует выражение (6.56). Таким образом, оптимальные процессы закупок (продаж) являются процессами минимальной диссипации, а условие (6.49) выделяет эти процессы. [c.239]
Из результата гл. 6 следует, что для каждого из полуциклов в оптимальном процессе поток ресурса должен быть постоянен, и, как следствие, равновесные цены покупок и продаж линейно изменяются во [c.248]
Требуется найти, для каких зависимостей n(x,u) в оптимальном процессе выполнено требование [c.398]
Так, к оптимизационным точным методам можно отнести методы теории оптимальных процессов, некоторые методы математического программирования и методы исследования операций. К оптимизационным приближенным методам относятся отдельные методы математического программирования, методы исследования операций, методы экономической кибернетики, методы математической теории планирования экстремальных экспериментов, эвристические методы. К неоптимизационным точным методам относятся методы элементарной математики и классические методы математического анализа, эконометрические методы. К неоптимизационным приближенным методам относятся метод статистических испытаний и другие методы математической статистики. [c.98]
Себестоимость детале-операций наиболее точно может быть рассчитана поэлементным методом. Поэлементный метод предусматривает прямой расчет не только затрат на основные материалы и -заработную плату производственных рабочих, но и большей части цеховых расходов по отдельным их элементам затрат на амортизацию и. ремонт оборудования и оснастки, на силовую электроэнергию, на наладку станков и т. д. Эти затраты определяются по отдельной детале-операций, что позволяет осуществлять выбор оптимального процесса и оборудования. Дифференциация и концентрация операций приводят к тому, что по отдельным вариантам приходится сравнивать не одну, а несколько операций. При этом должны сравниваться равноценные, с точки зрения объема работ, варианты. [c.194]
Особенностью смешанной экономики является то, что она как бы располагается между двумя крайностями чистым капитализмом и планово-централизованной системой. Однако такое понимание смешанной системы недостаточно, поскольку она представляет собой новый тип общественного устройства как результат современных достижений цивилизации на пути посткапиталистического развития. Здесь на базе рыночных отношений осуществляется оптимальный процесс диверсификации и интеграции экономических отношений в рамках одной системы с учетом активной роли государства. С точки зрения альтернативности эта система характеризуется следующими чертами 1) социально-ориентированная система, где налицо высшие достижения экономической и политической демократии, гражданского общества, качества личности, общественного согласия. Здесь относительно высокий и устойчивый жизненный уровень населения 2) в этой системе возникло новое качество собственности, проявляющееся во взаимопроникновении всех форм собственности как равноправных образований, а также многообразие этих форм 3) смешанная экономика приемлет такое государственное регулирование, которое обеспечивает оптимальное сочетание различных форм и методов, включая программно-целевые методы и методы государственного планирования на индикативной основе. [c.264]
ГАМИЛЬТОНИАН, ФУНКЦИЯ ГАМИЛЬТОНА — ПОНТРЯГИНА [Hamiltonian] — аналог Лагранжиана для задач математической теории оптимальных процессов. Обозначается буквой Н. В об- [c.59]
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ [optimal ontrol] — 1. Основное понятие математической теории оптимальных процессов (принадлежащей разделу математики под тем же названием — О.у.) означает выбор таких управляющих параметров, которые обеспечивали бы наилучшее с точки зрения заданного критерия протекание процесса или, иначе, наилучшее поведение системы, ее развитие к цели по оптимальной траектории. Эти управляющие параметры обычно рассматриваются как функции времени, что означает возможность их изменения по ходу [c.244]
ТРАЕКТОРИЯ [traje tory] — кривая, которую описывает точка при своем движении относительно выбранной системы координат. В экономико-математические исследования этот термин вошел из а.пп ра.тг.математической теории оптимальных процессов вместе с понятиями фазового пространства, фазовых коорди- [c.365]
УПРАВЛЯЮЩИЕ ПАРАМЕТРЫ (или управления) [ ontrol parameters] — понятиелга-тематической теории оптимальных процессов, динамического программирования переменные величины (функции времени), определяющие направление и скорость движения управляемой системы в фазовом пространстве. У.п. характеризуют решения, которые надо осуществлять в каждый данный момент времени из интервала между начальным и конечным состояниями системы. Допустимые управления удовлетворяют ограничениям задачи. Оптимальное управление (см.) обеспечивает достижение наибольшей эффективности управляемого процесса, т.е. максимального (при задаче максимизации) или минимального (при минимизации) значения целевой функции. [c.371]
ФАЗОВАЯ ТРАЕКТОРИЯ [phase traje tory] — см. Математическая теория оптимальных процессов, Траектория, Фазовое пространство. [c.374]
ФАЗОВОЕ ПРОСТРАНСТВО [phase spa e] — понятие математической теории оптимальных процессов, динамического программирования (пространство состояний) условное математическое пространство, размерность которого определяется числом параметров, характеризующих состояние системы в процессе ее преобразования, управляемого развития. Точка Ф.п. — кортеж, или вектор параметров. Изменение системы описывается перемещением точки по определенной траектории в Ф.п. — она называется фазовой. [c.374]
Понтрягин Лев Семенович (1908—1988), математик, академик АН СССР (1958). С 1939 г. — зав. отделом Математического института им. Стеклова, одновременно профессор МГУ. Имеет фундаментальные научные достижения во многих областях математики и теории управления. Создатель математической теории оптимальных процессов, в основе которой лежит т.н. принцип максимума Понтрягина. Почетный член многих зарубежных академий и научных обществ. Государственная премия СССР (1941), Ленинская премия (1966). [c.447]
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е. Ф. Математическая теория оптимальных процессов. — М. Физматгиз, 1961. [c.425]
Одному и тому же макросостоянию могут соответствовать различные микросостояния. Невозможность управления на микроуровне приводит к тому, что при контакте макроуправляемых систем происходит самопроизвольный обмен между составляющими их элементами, в результате которого состояния подсистем изменяются таким образом, что неопределенность микросостояния системы возрастает. Для того чтобы вернуть каждую из подсистем к прежнему состоянию, нужно приложить управляющее воздействие, что сопровождается затратой того или иного ресурса, полученного от окружающей среды, т.е. необратимостью процессов. Необратимость является важной особенностью макроуправляемых систем. От нее зависит область их реализуемых режимов, оптимальные процессы перехода из одного состояния в другое, равновесие в сложных системах и пр. Их свойства наряду с законами сохранения материи и энергии характеризуются балансовыми уравнениями, учитывающими изменения показателя необратимости. [c.3]
В силу сказанного общая структура оптимального процесса в ре-зервуарной системе такова. [c.72]
Когда базовое решение единственно и определяется равенством (2.101), оптимальный процесс состоит из двух адиабатических и одного изотермического участка с Т — Т. Для случая, когда базовых решений два, оптимальный процесс состоит из трех адиабатических [c.75]
Рассмотрим задачи о максимальной и минимальной работе в постановке, позволяющей включиить в рассмотрение не только тепломеханические системы, и исследуем характер оптимального решения как в задаче о максимуме полученной, так и в задаче о минимуме затра-ченой работы, а также в задаче о максимальной мощности. Покажем, что в оптимальном процессе для широкого класса систем независимо от законов тепло- и массообмена энтропия системы возрастает линейно либо кусочно линейно. Общие условия оптимальности конкретизируем для нескольких структур систем. [c.90]
