Вычисление средних значений [c.79]
На практике периодически возникают задачи, связанные с переоформлением финансовых соглашений на новых условиях или с заменой нескольких финансовых сделок на одну. Одним из методов решения такого типа задач при применении простых процентов является вычисление средних значений срока, ставки и капитала. [c.79]
Чтобы найти приемлемую формулу вычисления среднего значения, используем сначала формулу среднего арифметического, затем среднего геометрического и, наконец, среднего экономического. [c.55]
Формула для вычисления среднего значения ставки доходности любого портфеля, в котором w — это доля [c.219]
Обработка анкет заключается в вычислении среднего значения ранга проблем, дисперсии, приближенного значения доверительного интервала и доверительных границ. Среднее значение ранга определяется по формуле [c.154]
При изучении математического ожидания дохода отдельной сделки полезно рассмотреть вопрос о том, что определяет эту величину. Вернемся к формуле для вычисления среднего значения дохода сделок [c.193]
Аналогичное соотношение для процентных показателей можно получить, используя формулу для вычисления среднего значения до- [c.194]
Рассмотрим формулу для вычисления среднего значения дохода сделок (в %) для случая, когда в каждой сделке участвует весь капитал [c.206]
В методологии нормирования производственных запасов принято, что на основе вычисленного среднего значения запаса (в расчетном периоде) можно рассчитать его (запаса) норму, а также ее составляющие. В описанных ранее методах нормирования расчет среднего запаса в относительных величинах (в днях среднесуточного расхода в натуральном выражении) связывали в основном с продолжительностью интервала между поставками и с помощью этой величины определяли текущую составляющую нормы производственного запаса. При этом процесс поступления марки МР на склад предприятия можно рассматривать как входящий материальный поток, а процесс отпуска со склада в цех — как выходящий. [c.253]
| Рис. 63. Вычисленное среднее значение критической зоны YI пробито индикатором, и сформировался новый максимум А. Такое развитие событий -не редкость. | 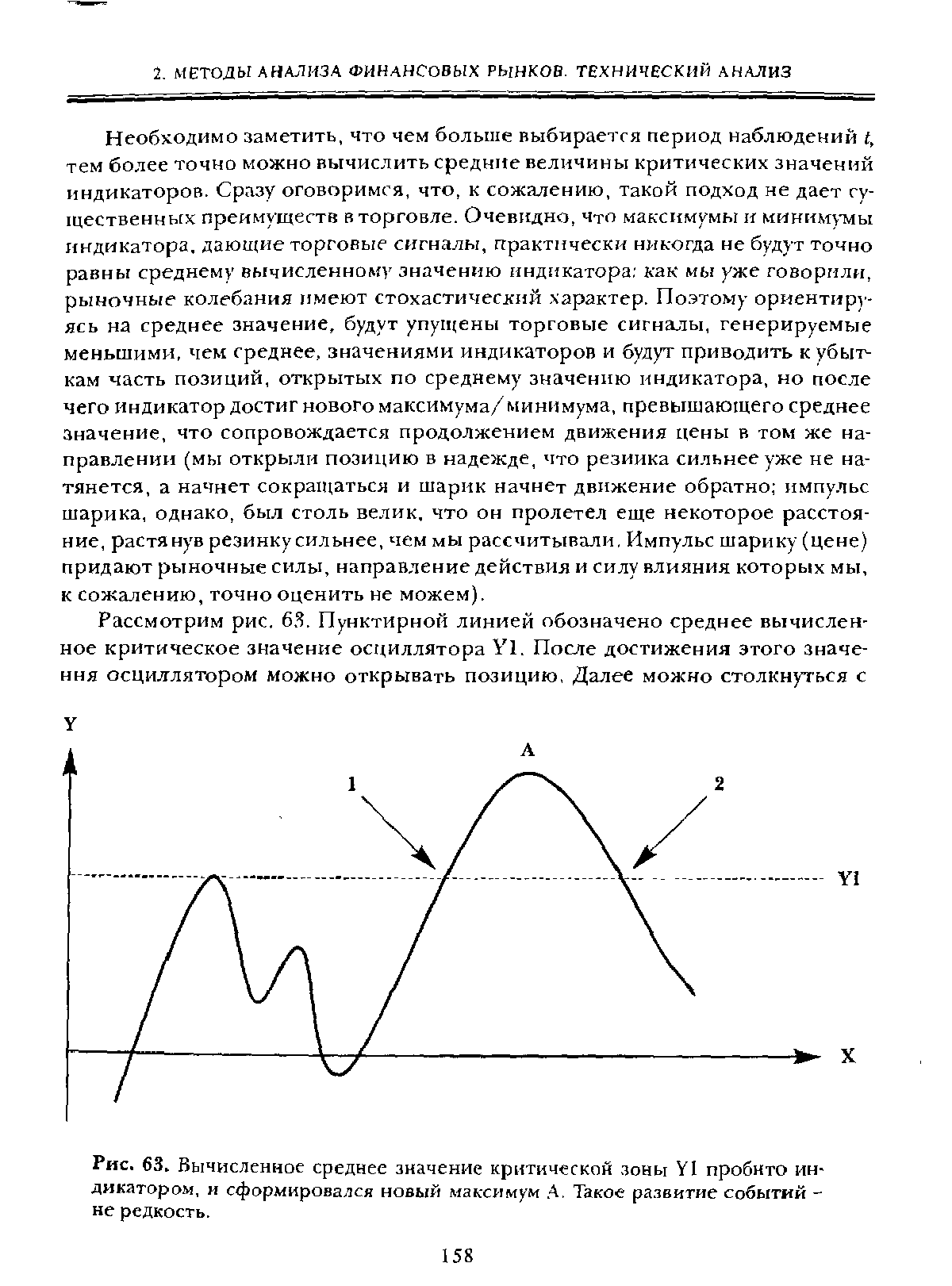 |
Следовательно, если номинаций ценных бумаг в портфеле не очень много, а доходности каждой из номинаций существенно различаются (геометрически точки отстоят на числовой оси далеко друг от друга), то даже при одних и тех же значениях вероятностей, приписываемых этим точкам , могут наблюдаться резкие смещения центра тяжести — значения математического ожидания доходности. В указанном смысле значительно более устойчивой оказывается медиана, поскольку геометрически она располагается ближе к центру группирования большинства точек . И в силу этого, например, медиана портфеля незначительно реагирует на изменение положения крайних — очень малых и очень больших — значений доходности. Однако следует иметь в виду, что вычисление медианы распределения — это существенно более сложная задача по сравнению с вычислением среднего значения распределения. К счастью, на практике в достаточно серьезном портфеле инвестиций обычно бывает много номинаций ценных бумаг. В силу этого распределение вероятности по значениям доходности [c.247]
Гармонизированный индекс потребительских цен,рассчитанный в соответствии с общими требованиями, которые были установлены Комиссией ЕС в отношении состава потребительской корзины, метода определения удельных весов товаров и услуг в потребительской корзине и метода вычисления средних значений. [c.34]
Вычисление среднего значения разности между выходным параметром k-ой эталонной ситуации Yk и оцениваемой ситуации Yev [c.191]
Другой метод построения диффузионного индекса заключается в вычислении средней продолжительности роста. Каждый индикатор, входящий в индекс, принимает значение количества месяцев, в течение которых происходит рост (положительные числа) или сокращение (отрицательные числа) производства. Средняя продолжительность роста определяется как средневзвешенный коэффициент этих величин. [c.96]
Научно обоснованным способом взвешивания достоинств исходных точек для вычисления прогнозируемых значений является алгоритм экспоненциальной средней, по которому значения весов х, по мере отдаления предшествующей точки от прогнозируемой убывают по экспоненте. [c.219]
Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. [c.77]
Для вычисления максимальных значений средних отклонений по модулю и квадратического построим таблицу отклонений (табл. 5.8). [c.114]
Приходится решать и обратную задачу вычисление необходимых значений факторных признаков для обеспечения планового или желаемого значения результативного признака в среднем по совокупности. Эта задача обычно не имеет единственного решения в рамках данного метода и должна дополняться постановкой и решением оптимизационной задачи на нахождение наилучшего из возможных вариантов ее решения (например, варианта, позволяющего достичь требуемого результата с минимальными затратами). [c.237]
Средняя арифметическая величина - это такое среднее значение признака, при вычислении которого общий объем признака в совокупности равномерно распределяется между всеми ее единицами. Например, предположим, что на предприятии работает п работников, причем величины заработной плата любых двух работников не совпадают. Для этой совокупности можно рассчитать размер заработной платы в среднем, т.е. такую ее величину, которая приходилась бы на одного работника, если бы весь фонд заработной платы (в данном случае это и есть общий объем признака) предприятия распределялся между всеми сотрудниками поровну. Формула для расчета средней арифметической ( 7 ) имеет вид [c.107]
При определении постоянных затрат нужно иметь в виду, что постоянными они являются только на протяжении определенного периода времени. Для вычисления их средних значений необходимо довольно точно представить будущую загрузку мощностей, а также использовать данные о затратах в прошлом. Следует также учитывать, что сохранение постоянных издержек на одном уровне возможно только в ограниченном диапазоне объемов производства. [c.97]
Метод, основанный на вычислении средней арифметической, или просто средней, обычно считается наиболее приемлемым. Он очевиден просто сложите имеющиеся значения и поделите сумму на их количество. Все просто, в том числе отработка данных таблиц частот. Однако, несмотря на всю эту простоту, зачастую этот метод наименее адекватен. Рассмотрим распределение заработной платы на рис. 1.17. Данная диаграмма иллюстрирует типичное распределение доходов всех работников крупной организации. Это положительно асимметричное распределение, с областью больших отклонений в правой части диаграммы. Доходы основной массы работников представлены в левой части диаграммы. Только несколько работников имеют доходы, представленные у верхней границы диаграммы. Вот эти-то несколько работников и искажают значение средней, и усредненное значение, полученное путем расчета арифметической средней, превышает приемлемо репрезентативное значение. Значение моды соответствует максимальному значению частот, представленных в распределении. При такой форме распределения это значение находится в области нижних значений заработной платы и поэтому также не является полностью репрезентативным. Значение медианы, как центральное значение, выступает в роли компромиссного решения и часто считается наилучшим показателем. На рис. 1.17 представлены значения средней, моды и медианы. Эти три показателя будут находиться в соответствии друг с другом, только если распределение данных симметрично. Если распределение отрицательно асимметрично, тогда последовательность значений меняется на обратную. Так, средняя будет наименьшим значением, а мода — наибольшим. На рис. 1.18 представлены три типа распределения с соответствующими показателями трех средних . Рисунки просто отображают форму каждого распределения. Так, проведенные кривые очерчивают контуры соответствующей гистограммы. Например, на рис. 1.18 (i) отображена форма, представляющая такое же распределение, что мы видим и на рис. 1.17. [c.30]
Вас не должна смущать эта внешне сложная математическая формула. Реальный механизм вычисления сглаженных значений с использованием экспоненциального сглаживания не сложнее тех вычислений, что мы применяли при определении значений скользящих средних в предыдущем разделе. Рассмотрим этот вопрос вновь на примере объемов продаж компании АПИ. В таблице приведены соответствующие объемы продаж, а также сглаженные значении при сглаживающей константе а = 0,1. [c.193]
Для ответа на этот вопрос необходим показатель, при расчете которого интегральный показатель эффективности функционирования ТЦ соотносится с каким-то другим показателем, отражающим общую эффективность функционирования предприятий, действующих самостоятельно. За этот последний показатель можно, например, принять среднее значение показателей эффективности, вычисленных для каждого предприятия. [c.55]
Таким образом, в случае наличия линейной связи между фактическими значениями переменных средний квадрат отклонения фактической переменной от вычисленной ух (принятой за среднее значение у) составит [c.49]
Приведение в соответствие (на основе принципа максимального правдоподобия) формул для вычисления среднего значения и разброса показателей качества с юс вероятностными законами также является одним из эффективных направлений повышения достоверности показателей качества. Так, при определении разброса показателя текучести расплава (ПТР) в партии следует отказаться от оцзнки его по относительному полуразмаху и перейти к среднему квадратическоыу отклонению шш коэффициенту вариация значений ПТР разовых проб. [c.94]
Оператор Р — проверка условия неполноты ассортимента продаваемой продукции /С2 — счетчик по видам продукции Р3 — проверка условия неполноты числа реализаций процесса /С4 — счетчик числа реализаций Ф5 — формирование случайной величины наличия или отсутствия отклонения (1 — имеется отклонение, 0 — отклонение отсутствует) фактического спроса (конъюнктуры) от договорных условий Рв — проверка условия наличия этого отклонения Ф7 — формирование случайной величины отклонения фактического спроса от договорных условий (отклонение может быть как в большую, так и в меньшую сторону) Р8 — проверка условия спрос больше, чем обусловлен договором Ф9 — формирование случайной величины изменения цены (0) или изменения объема продаж (1) Р10 — проверка условия изменения объема продаж по сравнению с договорным Лц — вычисление нового объема продаж Л12 — присвоение цене значения, обусловленного договором А 13 — присвоение объему продаж значения, обусловленного договором Л14 — присвоение цене значения, обусловленного договором А 15 — вычисление значения цены в связи с отклонением спроса от обусловленного договором Ф17 — формирование случайной величины изменения объема продаж при изменении спроса в меньшую сторону по сравнению с договорными условиями (1) или формирование изменения цены (0) Р1В — проверка условия изменения объема продаж Л19 — вычисление величины объема продаж при новых условиях Л20 — присвоение цене, по которой производится продажа средств производства, значения, обусловленного договором Л21 — вычисление цены, соответствующей спросу в новых условиях Л22 — присвоение величине объема продаж значения, обусловленного договором Я23 — определение значения максимальной цены г -го вида средств производства по всем реализациям процесса Я24 — определение минимального значения цены по всем реализациям процесса А 2Б — вычисление среднего объема продаж по всем реализациям процесса Л 2в — вычисление среднего значения цены по всем реализациям процесса Q27 — окончание расчетов и выдача результатов. ( По моделирующим алгоритмам имитации поведения предприятия в системе оптовой торговли составлены алгольные программы и произведен счет на ЭВМ БЭСМ-4 для 100 реализаций процесса и 10 продуктов. Анализ полученных параметров показал некоторые интересные особенности поведения предприятий в условиях оптовой торговли. Вместе с тем для исследования этих особенностей необходимо иметь результаты для значительно большего числа значений внешних и внутренних характеристик процесса. Возникает необходимость и в некотором усложнении имитационных моделей путем добавления таких ограничивающих факторов, как санкции за нарушение договоров и возможность вмешательства центра при несоблюдении договорных условий. Эти проблемы и определяют направление дальнейших исследований теоретических основ оптовой торговли. [c.93]
Метод базируется на вычислениях среднего значения прогнозируемой величены спроса за фиксированное количество периодов [c.120]
Имея т + 1) значений величины спроса в каждом из L периодов, можем применить процедуру усреднения этих значений в каждом периоде, используя либо процедуру вычисления средних значений, либо процедуру вычисления медианы Кемени. Таким образом, получаем усредненные значения спроса в L точках 5Г 52,..., SL. [c.138]
Умение производить взвешивание по относительным величинам структуры упрощает расчеты и сбор исходных данных. Кроме того, формулы вычисления средних значений по показателям структуры показывают зависимость среднего уровня не только от индивидуальных значений осредняемого показателя, но и от структуры совокупности. При изменении структуры меняется и средняя величина, хотя индивидуальные значения осредняемого признака могут оставаться прежними. Это [c.77]
Оценка резервов основывалась на текущих курсах доллара США и средних шестимесячных значениях цен золота на Лондонской бирже, если только дневная цена не опускалась ниже вычисленного среднего значения. Управление резервами в ЕВС передавали соответствующим центральным банкам, которые получали также и процентные доходы от использования долларовых резервов. Таким образом, по форме передача резервов в ЕВС была схожа с залогом, при котором распорядителем резервов остается Центральный банк. Вместе с тем, если размер переданных резервов оказывался ниже установленного обязательного 20-процентного уровня, то Центральный банк должен был платить проценты за недостающую сумму. Ставка процента определялась на основе средневзвешенных ставок денежного рынка в странах ЕВС, причем в качестве весов служил удельный вес валют корзины. Если размер E U, которыми располагал соответствующий эмиссионный банк, превышал обязательные резервы в ЕФВС (ЕВИ), то последний платил, в свою очередь, по упомянутой ставке проценты эмиссионному банку. [c.308]
Перейдем к рассмотрению средних вторичных (относительных) признаков. Сумма таких показателей сама по себе реальной величиной какого-либо признака в совокупности не является. Однако общее определение арифметической средней сохраняет силу и в этом случае. При вычислении таких средних величин необходимо, чтобы сохранялась сумма величины объемного признака, который является числителем при построении осредняемого относительного показателя. Например, при вычислении средней величины урожайности какой-либо сельскохозяйственной культуры (по формуле (5.2)) необходимо, чтобы общий объем валового сбора этой культуры остался неизменным при замене индивидуальных величин урожайности средней величиной. Нельзя менять реальную величину объемного признака - она является базой расчета средней. Чтобы выполнить указанное условие, в качестве весов при расчете средней величины относительного показателя необходимо принять значения того признака, который является знаменателем при определении относительного показателя. Так, при вычислении средней урожайности по совокупности хозяйств весами должны служить размеры площади данной культуры. [c.80]
Это свойство полезно использовать при расчете средней величины из многозначных и слабоварьирующих значений признака, например роста группы лиц х, = 179 см х2 = 183 см 3 = 171 см х = 180 см с5 = 169 см. Для вычисления среднего роста из каждого значения вычитаем 170 см и находим среднюю из остатков (9+ 13+ 1 + 10 - 1) 5 = 6,4. Средний рост = 6,4 + 170 = 176,4 см. [c.83]
Группа вспомогательных модулей дает возможность рассчитать обобщающие статистические характеристики. К последним можно отнести средние значения (у, х) общую и остаточную дисперсию-(о2, OO T) коэффициент вариации (У) коэффициенты парной (гух) и множественной корреляции (R). Последовательность вычислений этих величин проводится по известным в статистике формулам и при их исчислении затруднений не возникает. Поэтому рассматривать в данной статье эти алгоритмы модулей не представляется необходимым. Для краткости ниже приводится шифр модулей и формул, расчет которых он обеспечивает. [c.38]
Смотреть страницы где упоминается термин Вычисление средних значений
: [c.75] [c.145] [c.182] [c.34] [c.279] [c.315] [c.219] [c.281] [c.281] [c.189] [c.200] [c.180]Смотреть главы в:
Сборник задач по курсу финансовых вычислений -> Вычисление средних значений
