Задача параметрического программирования имеет следующий вид [c.131]
На первом этапе решается задача параметрического программирования следующего вида [c.58]
Задачи параметрического программирования [c.516]
Дальнейшим обобщением этих задач является задача параметрического программирования, в которой от параметра / зависят коэффициенты при неизвестных в целевой функции, коэффициенты при неизвестных в системе ограничений и свободные члены системы ограничений. [c.517]
Задача параметрического программирования с параметром в свободных членах системы ограничений с помощью теории двойственности сводится к рассмотренному выше случаю. [c.521]
Подобного рода задачи называются задачами параметрического программирования. [c.146]
Задачи параметрического программирования являются обобщением задач линейного программирования. Это обобщение состоит в том, что исходная информация задач параметрического программирования изменяется линейно в зависимости от некоторого параметра. Если предположить, например, что произведенная предприятием продукция подлежит хранению, то ее стоимость будет складываться из двух частей [c.375]
Проведем геометрическую интерпретацию задачи параметрического программирования. Полагая t = а и ограничиваясь только двумя переменными, получаем обычную задачу линейного программирования (рис. 12.1). [c.376]
При / = ос изменяются коэффициенты целевой функции, геометрически это значит, что прямая, соответствующая Za, повернулась на некоторый угол. Из рис. 12.1 следует, что Za max достигается в точке AI, a Za max - в точке А2. Естественно предположить, что при некотором значении t максимальное значение достигается одновременно в точках А1 и А2. В этом случае прямая, соответствующая целевой функции, параллельна стороне А А2 многоугольника решений. Фиксированное значение t является граничной точкой между двумя соседними интервалами отрезка [а, Р]. Исходя из изложенного, задачу параметрического программирования с двумя переменными можно решить графически. [c.376]
| Рис. 12.2. Геометрическое решение задачи параметрического программирования | 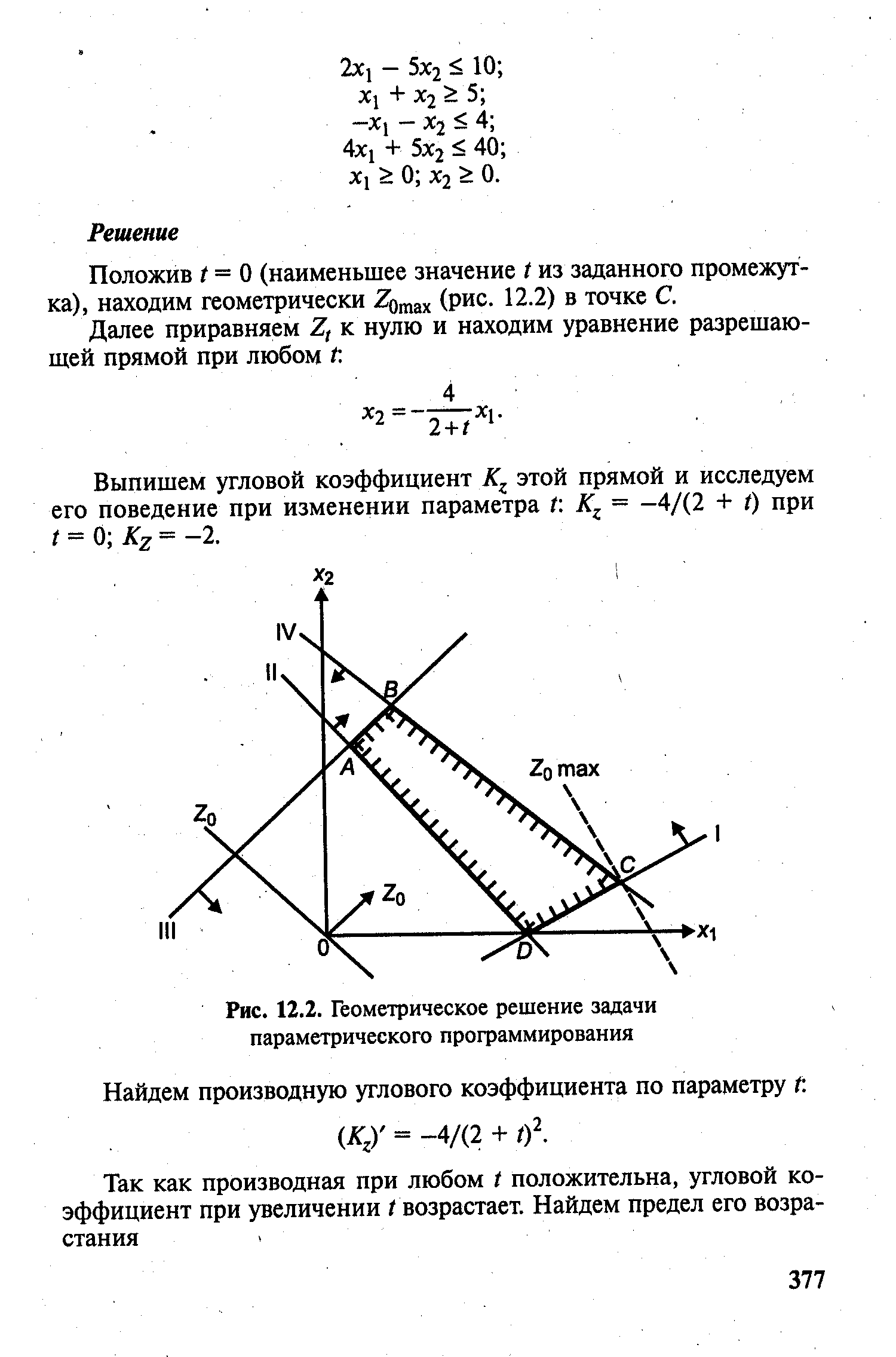 |
Форма симплекс-таблицы для решения задачи параметрического программирования [c.379]
Пример 12.2. Решить задачу параметрического программирования [c.382]
Другой путь применения методов взвешивания состоит в использовании методов линейного параметрического программирования. Сначала находят точку эффективного множества, максимизируя один из показателей (скажем, находится точка А см. рис. 6.9), затем с помощью методов параметрического линейного программирования определяется, как надо изменить вектор весов,, чтобы получить соседнюю эффективную точку, и т. д. Достоинство этого метода состоит в том, что выбор весов отражает структуру задачи, а сложность — в том, что приходится организовывать процесс таким образом, чтобы просмотреть все эффективные вершины. Конечно, довести до конца такой процесс удается только тогда, когда число эффективных вершин не слишком велико. Кроме того, методы нара-метрического программирования имеют тот же недостаток, что и методы сеток (см. рис. 6.10). [c.311]
Во многих задачах производственного менеджмента исходные данные зависят от некоторого параметра. Введение параметра обычно отражает некоторую реальную ситуацию. Рассмотрим естественное обобщение нашей задачи производственного планирования, когда исходные данные считаются не постоянными величинами, а функциями, зависящими определенным образом от некоторого параметра. Приведем несколько постановок задач линейного параметрического программирования. [c.516]
Задача минимизации затрат на проект - это оптимизационная задача, которая ставится как задача параметрического линейного программирования [c.135]
Алгоритм решения Л-задачи, приведенный в предыдущем параграфе, сводится в нашем случае к решению последовательности задач. параметрического квадратичного программирования вида [c.233]
Обозначим через oj критические значения параметра со, а через jj(t)—соответствующие решения задачи линейного параметрического программирования, o = oo< oi<.... <
Выбор в заданном диапазоне длин точного размера материала, дающего минимум отходов при использовании смешанных раскроев, составляет типичную задачу параметрического линейного программирования. Этот вопрос рассматривается в статьях [c.232]
Рассматривается моделирование экономических систем с использованием марковских случайных процессов, моделирование систем массового обслуживания, методы и модели корреляционно-регрессионного анализа и прогнозирования временных рядов экономических показателей. Приводятся оптимизационные методы и модели в управлении экономическими системами, линейное, динамическое, параметрическое и целочисленное программирование, а также транспортные задачи линейного программирования, теория игр и принятие решений. [c.2]
Левитин Е.С. О дифференциальных свойствах оптимального значения параметрических задач математического программирования. - ДАН СССР, т. 215, № 4, с. 792 - 795. [c.437]
Приведенный пример исследования чувствительности оптимального плана по отношению к изменению параметров задачи является весьма простым. Очевидно, что существуют и более сложные задачи, в которых, например, исследуются совместные вариации параметров разных типов. Они составляют предмет специального раздела исследования операций, получившего название параметрического программирования. Заинтересованный читатель может получить дополнительную информацию по данному предмету в [1, 6]. [c.68]
В каждом из перечисленных направлений оптимального программирования в свою очередь могут возникать задачи, требующие специальных методов решений. К числу таких задач относятся задачи, в которых исходные условия либо могут быть заданы несколькими дискретными значениями — задачи целочисленного программирования, либо исходные условия изменяются в определенных пределах — параметрическое программирование. [c.165]
Решение взаимной задачи В, как следует из вышеизложенного, предполагает знание в общем случае априори неизвестного максимально достижимого уровня С целевой функции исходной задачи А. Однако теория взаимных задач позволяет решать соответствующие задачи в итеративном режиме параметрического программирования относительно возрастающего параметра С. [c.42]
Параметрическое программирование — раздел математического программирования, изучающий задачи, отличие которых от других задач состоит в следующем. Коэффициенты их целевой функции, или числовые характеристики ограничений, или те и другие, предполагаются не постоянными величинами (как, например, в линейном программировании), а функциями, зависящими от некоторых параметров. Причем чаще всего эта зависимость носит линейный характер. Параметрическое программирование позволяет в ряде случаев приблизить к реальности условия задач линейного программирования. Например, если коэффициенты целевой функции представляют собой цены некоторых продуктов, то вполне естественно бывает предположить, что эти цены не постоянны, а являются функциями параметра [c.221]
Параметрические задачи линейного программирования [c.214]
Параметрическая задача линейного программирования возникла в связи с необходимостью изучить поведение оптимального решения задачи линейного программирования в зависимости от тех или иных изменений коэффициентов целевой функции. [c.214]
Таким образом, всегда можно найти множество всех значений параметра t, при которых данное опорное решение является оптимальным решением параметрической задачи линейного программирования. [c.215]
Основным недостатком этого метода является огромное число задач оптимизации, которые необходимо решить для нахождения более или менее разумного числа эффективных точек. Так, в задаче с пятью критериями при Т = 4 (очень грубая сетка) необходимо решить 5-54 = 55 = 3125 задач. Если модель и критерии линейны, то эту трудность удается в какой-то степени обойти путем использования методов параметрического линейного программирования. Как и в других методах, основанных на представлении эффективного множества в виде совокупности точек, здесь возникает проблема представления этих точек ЛПР. [c.314]
Отдельные разделы экономико-математических методов изучают методы решения задач целочисленного, параметрического, дробно-линейного программирования. [c.104]
В постановке (3.74)-(3.79) искомыми (оптимизируемыми) величинами в подзадачах (3.75) — (3.79) являются компоненты векторов -/Г,, и К — случайные величины a iv и . При формировании подзадач эти величины в ограничениях вида (3.77), (3.78) оказываются только в правой части, что обеспечивает линейный вид их детерминированных аналогов. При линейном виде функции H(aiv), описывающей параметрические связи, в соответствии с рассмотренными в [47] случаями детерминированный аналог задачи (3.74) —(3.79), в отличие от (3.73), после соответствующих преобразований может быть представлен в виде задачи обобщенного линейного программирования, решение которого осуществляется на базе известного алгоритма [16]. [c.72]
Кроме того, есть еще одна проблема целевого программирования — выбор метрики. Чаще всего при решении прикладных задач используют какую-либо метрику из следующего параметрического семейства [c.164]
Параметрическое линейное программирование. Алгоритм для исследования задачи с параметром в целевой функции. Характер зависимости оптимального значения критерия от параметра. Задачи с параметром в правой части ограничений. [c.47]
С вычислительной точки зрения применение закона оптимального планирования с прогнозом приводит к необходимости решать для определения множества Р(л) п задач математического программирования (4.2.4), размерность которых равна размерности состояний отдельных элементов. Решения этих задач (они параметрически зависят от планов л,-, i ЕЕ I элементов) нужно подставить в основную задачу оптимизации (4.7.9), (4.7.10) и решать ее относительно плана л. В общем случае — это задача нелинейного параметрического (относительно плана я) программирования. Таким образом, переход от принципа оптимального планирования (4.5.1), (4.5.2) к принципу оптимального планирования с прогнозом состояний (4.7.9), (4.7.10), с одной стороны, приводит к уменьшению размерности решаемых задач математического программирования, а с другой стороны — к необходимости решения задач параметрического программирования, что несомненно вызывает усложнение используемых для решения вычислительных алгоритмов. Значение критерия эффективности К (2ОПП) механизма функционирования 2° определяется следующими выражениями [c.144]
ПАРАМЕТРИЧЕСКОЕ ПРОГРАММИРОВАНИЕ [parametri al programming] — раздел математического программирования, изучающий задачи, отличие которых от других задач состоит в следующем. Коэффициенты яхцелевой функции, или числовые характеристики ограничений, или и те и другие, предполагаются не постоянными величинами (как, напр., в [c.258]
Рассмотрим, например, проблематику двухуровневой технологии принятия решений. Двухуровневое программирование изучает задачи принятия решений несколькими неравноценными партнерами, один из которых является лидером, а все прочие — ведомыми. Лидер оптимизирует свою целевую функцию (функцию верхнего уровня) при ограничениях, включающих в себя реакцию ведомой стороны (сторон) на его решения. Реакция ведомой стороны описывается задачей математического программирования нижнего уровня, целевая функция и ограничения которой параметрически зависят от переменных верхнего уровня. В более строгой записи задача двухуровневого программирования выглядит следующим образом [c.70]
Шор Н. 3., Щепакин М. Б. Задачи многоэтапного стохастического программирования в параметрической форме. — В кн. Теория оптимальных решений. Труды семинара. Вып. 3, Кие в, 1969, с. 64—73. [c.393]
Смотреть страницы где упоминается термин Задачи параметрического программирования
: [c.16] [c.129] [c.214]Смотреть главы в:
Производственный менеджмент -> Задачи параметрического программирования
