Пусть производственная функция дифференцируема. В точке г, где /(г)>0, определим локальную эластичность масштаба е(г) как [c.123]
Если функция f(x) дифференцируема в точке х, то она и непрерывна в этой точке. Если она дифференцируема в каждой точке некоторого промежутка, то говорят, что она дифференцируема на этом промежутке. Если, кроме того, производная J[x) непрерывна на данном промежутке, то функция f(x) называется непрерывно дифференцируемой на этом промежутке. [c.92]
Сначала предположим, что функции /о и /а- непрерывно дифференцируемы в точке х , а само это решение находится внутри Vx. Заменим, пользуясь малостью б, функции /о и /а- линейной частью их разложения в ряд Тейлора [c.330]
Первое из этих условий для дифференцируемой в точке С — О функции достижимости может быть выполнено за счет выбора АО из условия [c.358]
Другими словами, / дифференцируема в точке с, если /(с + u) может быть сколь угодно хорошо приближена аффинной функцией от и. Отметим, что любая функция / может быть дифференцируемой только во внутренней точке или на открытом множестве. [c.119]
Ранее (в 2) было показано, что функция может быть непрерывна в точке с, однако разрывна в близких точках более того, она может не быть определена вблизи с. Если функция дифференцируема в с, то она должна существовать в окрестности с, однако она не обязана быть дифференцируемой или даже непрерывной в этой окрестности. Например, функция ф 1R, — > R, такая что [c.120]
Пусть S С Rn. Функция / S — > Rm дифференцируема во внутренней точке с G тогда и только тогда, когда каждая компонента / дифференцируема в точке с. При этом г-я компонента дифференциала d/( u) есть dfi( -u)(i = 1,.. . , m). [c.120]
Пусть / S —> Rm и g S —> Rm дифференцируемы в точке с Е S С Rn. Тогда функция h = / + g дифференцируема в с и d/i( и) = d/( и) + dg( -u). [c.121]
Пусть функция / S —> Rm, S С Rn дифференцируема в точке с G 5, и ее дифференциал равен d/( и) = Л (с) и. Предположим, что существует другая матрица Л (с), такая что d/( u) = А (с) и. Тогда Л (с) = Л (с). [c.121]
Пусть / S —> Rm — функция, определенная на множестве S С Rn, и пусть с — внутренняя точка S. Если все частные производные Dj/ существуют в некоторой n-мерном шаре В (с) и непрерывны в с, то / дифференцируема в точке с. [c.128]
Обратите внимание, что в то время как непрерывность и дифференцируемость функции определяются в точке, непрерывная дифференцируемость определяется на открытом множестве. Естественно, что по теореме 7 из непрерывной дифференцируемости следует дифференцируемость 1. [c.130]
Рассмотрим вещественную функцию ф S —> R, которая дифференцируема в точке с из S С Rn, т.е. существует вектор а, зависящий от с, но не от и, такой что [c.142]
Функция ф дифференцируема только в точке (0, 0). Частная производная DI равна нулю в начале координат и в любой точке из R2, где у иррационально в других точках она не определена. Аналогично, D20 равна нулю в начале координат, а также в каждой точке из R2, где х иррационально в других точках она не определена. Следовательно, ни одна из частных производных не дифференцируема ни в одной точке из R. С другой стороны, существует единственная матрица В (нулевая матрица), такая что разложение Тейлора второго порядка (3) выполняется в точке с = 0. Конечно, мы не хотим сказать, что ф дважды дифференцируема в точке, когда ее частные производные не дифференцируемы в этой точке [c.143]
Давайте теперь вычислим второй дифференциал вещественной функции ф S — > R, где S есть подмножество Rn. В предположении, что ф дважды дифференцируема в точке с 5, можно определить [c.146]
Пусть ф S —> R — вещественная функция, определенная на множестве S С Rn, и предположим, что ф имеет локальный минимум во внутренней точке с G S. Если ф дифференцируема в точке с, то [c.164]
Пусть F = (fst) есть дифференцируемая вещественная матричная функция размера т х р от матрицы X вещественных переменных размера п х q. Тогда матрицей Якоби функции F в точке X называется следующая тр х nq матрица [c.227]
Теорема. Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна. [c.111]
Будем говорить, что функция имеет непрерывные частные производные в точке М(ж, у), если z — /(ж, т/) имеет частные производные zx (ж, у), zy (ж, у) в окрестности точки (ж, у), причем эти производные непрерывны в самой точке (ж, у]. Такая функция является дифференцируемой в точке (ж, у). (Вообще же, понятие дифференцируемости шире, чем существование непрерывных частных производных. Однако практически все функции, рассматриваемые в социально-экономической сфере, обладают непрерывными частными производными. Поэтому точного определения дифференцируемости нам не понадобится.) [c.288]
Это значит, что на у достигается наименьшее значение функции Н(Х, ). Как было отмечено в пп. 12.9, 21.2, функция Н(Х, ) является выпуклой. Следовательно, если эта функция дифференцируема (в том смысле, что она имеет первые частные производные по всем компонентам стратегии у игрока 2), то, согласно сказанному в п. 21.2, наименьшее ее значение должно быть аналитическим минимумом в той опорной гиперплоскости, в которой лежит стратегия >> (см. п. 22,4). [c.139]
Если функция Дх) дифференцируема в точке х0, то она непрерывна в этой точке. [c.52]
Геометрический смысл производной. Пусть у =Дх) - дифференцируемая в точке х0 функция, график которой изображен на рис.З.За. [c.52]
Если данная функция дифференцируема в каждой точке интервала (а Ь), то пишут dj(x) =/(х)Дх или dy = /Дх. [c.54]
Пусть функция прибыли тс(-) непрерывно дифференцируема в точке р е int(P). Тогда [c.129]
Теорема 8.1. Если функция г=/(л , у) дважды дифференцируема в точке Л/о (хй, yu),-io ее смешанные производные в этой точке равны. [c.159]
Функция y = f(x) называется дифференцируемой в точке х, если в этой точке ее приращение Д = / (х +- eta) — — / (л ) преДставимо в виде Д у — А (х) dx + a (d ), где Л (л ) — постоянная, a a(dx) = o(dx) при dx— -0, т. е. является бесконечно малой высшего порядка малости по сравнению с dx. [c.113]
Если функция / (л ) дифференцируема в точке х, то она и непрерывна в этой точке. [c.113]
Функция f(x) дифференцируема в точке х тогда и только тогда, когда в этой точке существует конечная производная f (х). При этом A (x) = f (х), так что dy = f (x)dx. [c.113]
Предположим, что М0 — неособая точка условного экстремума функции /(Л ) на множестве V. Если функции f(M) и Ф/(М), i— 1, 2,. . . , k, k+1,. ..,/, дифференцируемы в точке Мв, то эта точка является условно стационарной точкой функции f(M) на множестве V. [c.146]
Если функции f(M) и ФДМ) t == 1, 2,. .., т, дифференцируемы в точке М0 R , то эта точка является оптимальным решением задачи (9.59)—(9.61) тогда и только тогда, когда она является точкой Куна—Таккера для этой задачи. [c.231]
| Рис. 9.9. Функции достижимости, для которых расширение Лагранжа эквивалентно a — недифференцируемая в точке С = 0 б— дифференцируемая в точке С = О | 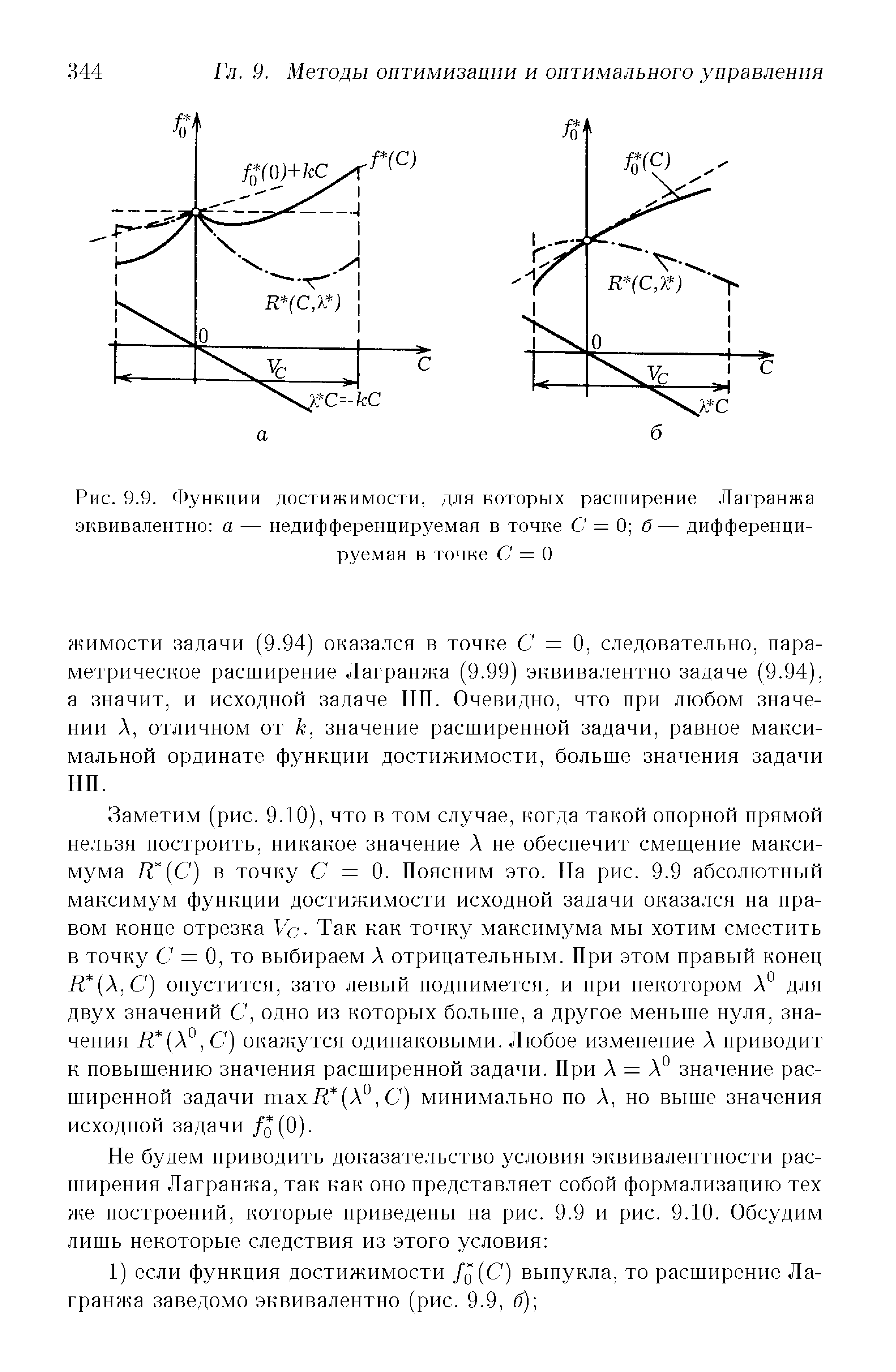 |
Пусть F дважды дифференцируемая т х р матричная функция от п х q матрицы X. Матрицей Гессе 1 функции F в точке X назовем матрицу размера mnpq x ng, определенную по следующей формуле [c.245]
Пусть ф дважды дифференцируемая вещественная функция от матрицы X размера п х q. Тогда для дифференциала второго порядка и матрицы Гессе функции ф в точке X выполняются следующие два соотношения [c.249]
Геометрический смысл дифференциала. Пусть у = Дх) - дифференцируемая в точке х0 функция, график которой изображен на рис. 3.4а, МйТ- касательная к графику функции у = Дх) в точке Af0 с абсциссой Хд. Рассмотрим ординату этой касательной, соответствующую абсциссе х + Дх. Из прямоугольного треугольника ДАО/Т находим NT= A Mga, но M0N= Дх и tga = /(х.). Поэтому NT = /(х0)Дх = df xj. Таким образом, дифференциал функции у = Дх) в точке х0 равен приращению ординаты касательной, проведенной к графику этой функции в точке (х0 Дх0)), соответствующему приращению ее абсциссы х0 на Дх. Можно показать, что этот вывод не зависит от расположения графика функции и касательной на координатной плоскости (см. рис. 3.46). [c.55]
Введенные упрощающие условия (ГРАД) для ТБ2 на самом деле избыточны. Во-первых, дифференцируемость может быть отброшена. Во-вторых, неотрицательность grad щ > 0 вытекает из Xi e int(Xi). В-третьих, это условие на внутренность может быть ослаблено, так что (ГРАД) в целом можно заменить таким легким условием [Пусть К+— множество товаров, по которым целевая функция возрастает в точке х хотя бы у одного участника. Тогда либо 1)найдется участник, для которого Xi D Ml+ х > 0 Vf e К+, либо 2)у каждого участника целевые функции строго возрастают по товарам Vf e К+.] ("ресурсная связность"). Читатель может проверить справедливость этого усиления теоремы ТБ2 пользуясь вариантом теоремы К-Т без дифференцируемости. [c.19]
Пусть функция /(М) определеша в некоторой окрестности точки М , М0 R"- Функщиш / (М) называется дифференцируемой в точке М0, еслш полное приращение А/ в этой точке имеет следующий вид. [c.136]
Функция / (М ) = х + jrjg дифференцируема в точке Af0(l —2). В самом деле, [c.137]
Обычно относительно производственной функции (2.8) делают предположение, очень удобное с математической точки зрения,— предположение о непрерывном изменении переменных х и достаточно плавном изменении выпуска при изменении затрат ресурсов. В математической форме эти предположения имеют следующий вид функция (2.8) задана при всех неотрицательных значениях составляющих вектора х (как принято говорить, на неотрицательном ортанте) и является непрерывной (или нужное число раз дифференцируемой) функцией своих аргументов. На практике ресурсы и продукция зачастую не могут меняться непрерывно — их количество дискретно и измеряется, например, в штуках. Описание с помощью переменных, принимающих любые вещественные значения, и непрерывных функций означает в таких-случаях, что число выпускаемых и потребляемых единиц достаточно велико, чтобы дискретностью МОЖНО было пренебречь. [c.70]
Затем производим итерации с малым шагом . При малом шаге используется идея процедуры Кифера — Вольфовица, смысл которой состоит в следующем. Известно, что для нахождения экстремума функции / (х), непрерывно дифференцируемой в области задания и имеющей экстремум в точке X=XQ, можно использовать градиентный метод, описываемый рекуррентным соотношением [c.48]
