Некооперативные игры делятся на игры в нормальной форме (когда каждый игрок может сделать только один ход) и позиционные (в которых игроки могут делать несколько выборов, или ходов). Одним из игроков в позиционных играх может быть случай . [c.373]
Позиционными играми удобно описываются условия таких игр, как шашки, шахматы, карточные игры. [c.373]
Дж. фон Нейманом была показана сводимость позиционных игр к играм в нормальной форме. [c.373]
Начальный характер курса и его ориентация- на читателя-экономиста предопределили и отбор включенного в нее материала. Так (даже если говорить только об элементарных вопросах теории игр), за его рамками осталась теория динамических (позиционных) игр, как менее важная для экономистов, а также вопросы устойчивости конфигураций в кооперативной теории и теория игр без побочных платежей (в том числе — теория арбитражных схем), которые следует рассматривать при дальнейшем, более глубоком изучении теории игр. [c.4]
Разница между внутридневной и позиционной игрой — как между пилотированием самолета и вождением автомобиля. Вы можете с удобством расположиться за рулем, слушать музыку, говорить по сотовому и даже полистать журнал на светофоре. Управляя самолетом, себе этого не позволишь. [c.162]
Сколько времени необходимо уделять анализу рынка и планированию игры Трейдер-новичок должен изучать основы каждую минуту, когда не спит. А сколько времени вам потребуется на следующем этапе, когда вы подниметесь до уровня полупрофессионала Речь идет о позиционной игре, а не о внутридневной, которая требует постоянного присутствия у экрана. Ответ зависит от того, как быстро вы работаете и на скольких рынках играете одновременно. [c.274]
Игры подобного типа, где задается последовательность принятия решений игроками, называются позиционными играми число игроков и шагов в них может равняться 2 (как в нашем примере), 3 и т.д. К позиционным многошаговым играм двух лиц, где игроки принимают решения, зная о всех предыдущих решениях партнера, можно отнести, например, шахматы и шашки. [c.240]
В силу отмеченных особенностей структуры позиционной игры ее более наглядно представляет не матрица выигрышей, а дерево решений (или, в общем случае, граф решений), приводящее игроков из исходной позиции в конечные. Так, описанную игру Вступление на рынок можно представить следующим деревом (рис. 13.9), ветви которого соответствуют решениям партнеров, а у каждой из висячих вершин указаны выигрыши игроков (как и ранее, первыми указаны выигрыши Фирмы 1, в млрд.руб.). [c.240]
Однако в позиционной игре необходимо учитывать, что Фирма I принимает решение, уже зная о решении, принятом Фирмой 2. При этом менеджеры Фирмы 2, которая должна сделать первый шаг, при выборе своей стратегии могут рассуждать следующим образом "Если мы не вступим на рынок со своей продукцией, то в любом случае мы ничего не потеряем. С другой стороны, если мы решим внедриться на рынок, не исключено, что Фирма I сохранит объем своего производства, и для нас это обернется потерями в 2 млрд.руб. " Затем, следуя принципу максимизации своего минимального выигрыша, Фирма 2 должна была бы избрать стратегию "Воздержаться от вступления на рынок" - ее прибыль в этом случае максимальна (0 млрд.руб. больше, чем -2 млрд.руб.). [c.241]
В чем особенность позиционных игр Как степень правдоподобности угроз одного из партнеров влияет на исход позиционной игры [c.244]
Легко видеть, что в соответствии с определением стратегий в позиционной игре, любая стратегия игрока в позиционной игре индуцирует стратегию в под-игре, получающуюся сужением исходной стратегии на информационные множества игрока, оказывающиеся в под-игре. [c.97]
Определение 4.2.1 Пара (<т, /л), состоящая из набора стратегий и системы представлений называется последовательным равновесием в позиционной игре ГЕ, если (1) набор стратегий а последовательно рационален при данной системе представлений ц (2) существует последовательность вполне смешанных стратегий (то есть стратегий, в которых каждая чистя стратегия играется с положительной вероятностью) ak L1 такая, что Нгщ-юо rk = r, причем ц = Нгщ-юо jj,k, где jj,k — представления, выводимые из набора стратегий ak no правилу Байеса. [c.153]
| Рис. 6.2. Схема позиционной игры | 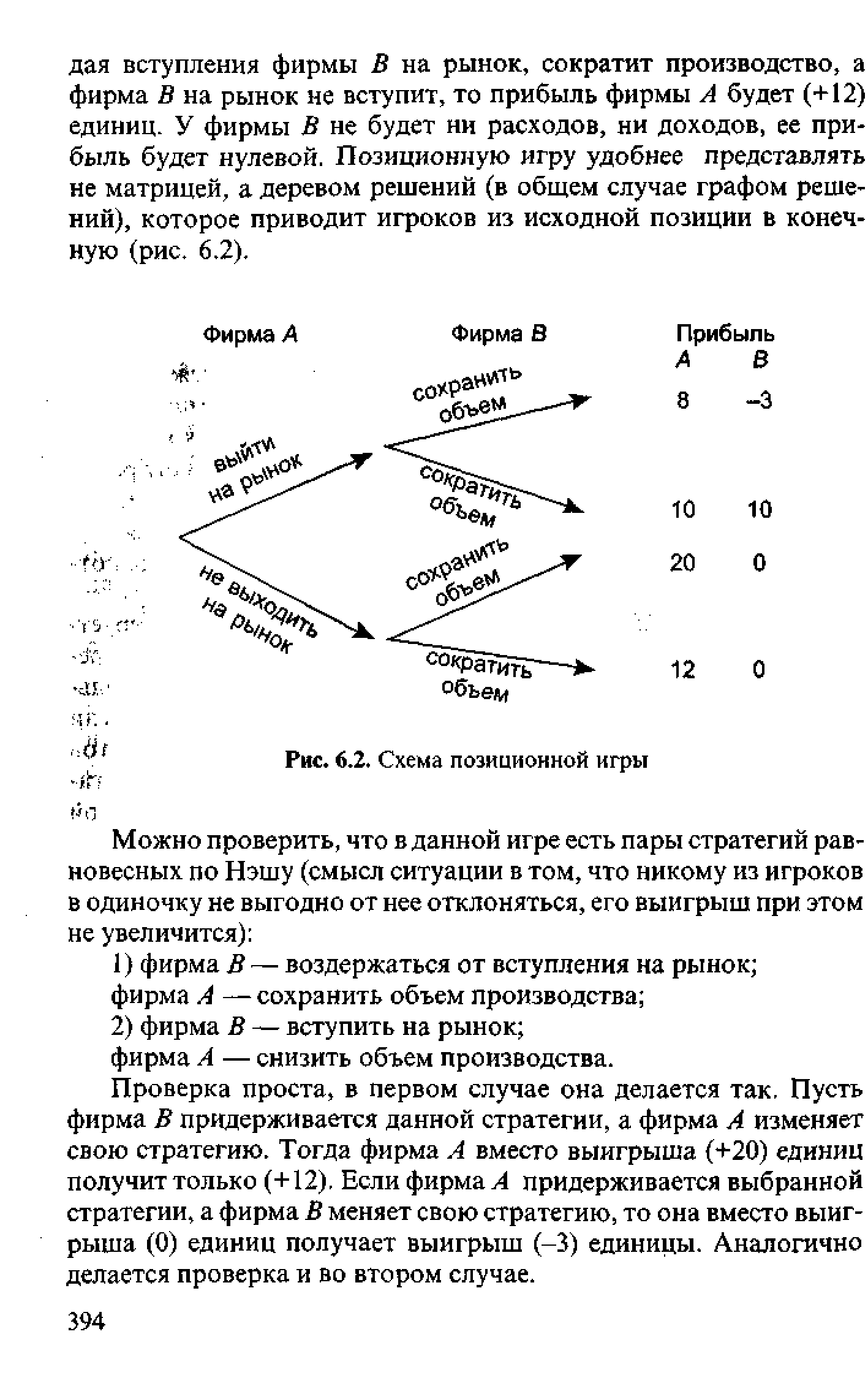 |
Большинство позиционных трейдеров на фьючерсном рынке играют, опираясь на промежуточную, а не на основную тенденцию. Краткосрочные колебания в этом случае чрезвычайно важны как средство определения наиболее подходящего момента для открытия и закрытия позиций. Например, в условиях промежуточной тенденции на повышение, [c.37]
Позиционный игрок должен начать игру и держать позицию, пока недельный тренд не изменится. Краткосрочный игрок может извлекать прибыль по сигналам второго экрана. Например, если игрок играет на повышение и индекс силы становится положительным или стохастика повышается до 70 процентов, то он может продать, извлечь прибыль и присматривать следующую возможность купить. [c.140]
Позиционная форма представляется деревом игры, кото- [c.20]
Позиционная форма игры [c.83]
Определение 2.1.1. Игра в позиционной форме называется [c.88]
ДЕРЕВО ИГРЫ [game tree] — способ описания игры с помощью графа "дерево", последовательно по ходам фиксирующего, какой информацией располагают игроки перед каждым ходом, какие варианты они могут выбирать и какими могут быть предельные размеры платежей в конце игры. Игра, описываемая с помощью подобного "дерева", называется игрой в развернутой (экстенсивной) форме, а иногда — позиционной игрой. [c.77]
См. также Антагонистические игры, Бескоалиционные игры, Бесконечные игры, Биматричиая игра, Дифференциаль-ные игры, Игра с "природой ", Игры с непротивоположными интересами, Игры с ненулевой суммой, Игры с нулевой суммой, Конечные и бесконечные игры, Кооперативные игры, Матричные игры, Некооперативные игры, Парные игры, Позиционные игры, Прямоугольные игры. [c.112]
Дальнейшие успехи Харшаньи и Зелтена в теории игр были сделаны на пути отказа от жестко заданных моделей игр в нормальной форме, возвращения к моделям многошаговых позиционных игр и изучения динамических процессов принятия решения. [c.376]
До 1965 г. предлагаемые одними специалистами подходы к моделированию игр с не полностью известными условиями не были популярны у других. Дж. Харшаньи предложил моделировать такие игры как начинающиеся с лотереи, разыгрываемой природой. Правила лотереи известны всем игрокам. Результаты лотереи полностью определяют черты игроков, при этом игроку становятся известны только результаты лотереи о нем самом. Таким образом, задача была сведена к позиционной игре с неполной информацией, и в настоящее время такой подход является общепринятым. Значительный вклад в обоснование и углубление такого подхода принадлежит Р. Зел-тену. [c.376]
Методы определения различных принципов оптимальности в кооперативных играх и нахождения для них соответствующих решений весьма разнообразны. Идея сводить кооперативные игры к некооперативным принадлежит Нэшу и известна как программа Нэша . Дж. Харшаньи одним из первых для решения проблем теории кооперативных игр начал строить различные модели принятия решений в кооперативных играх в виде позиционных игр и игр в нормальной форме. До выделения единственной ситуации равновесия такое моделирование к однозначному ответу в теории кооперативных игр не приводило, что видно на описанном выше простейшем примере игры торга 2 лиц. Определение единственной ситуации равновесия снимает эту проблему. [c.377]
Доказательство см. в монографии А. Вальда "Статистические решающие функции" (русск. пер. в кн. "Позиционные игры" М., "Мир", 1967, с. 367). В основе этого доказательства лежат рассуждения, известные для случая х = у = R как первая теорема Хелли (см., например, учебник Б.В. Гнеденко "Курс теории вероятностей", М., Гос-техиздат 1961, с. 234). [c.114]
Эти оценки важны при позиционной игре, но они еще важнее для дейтрей-деров. Помните, что при игре на понижение вы продаете, чтобы открыть сделку, и покупаете, чтобы закрыть. Рейтинги проводятся также, только в обратном порядке. [c.260]
С утра надо знать, чем и как будешь торговать. Это касается прежде всего позиционной игры, так как дейтрейдерам приходится действовать по ситуации, следя за экраном и мгновенно реагируя на изменения котировок. [c.264]
Иллюстрацией этого могут служить ситуации, складывающиеся в различных позиционных играх. Пусть разыгрывается некоторая шахматная партия. Любая позиция, сложившаяся в процессе игры на доске, есть площадка некоего лабиринта, коридорами которого являются все возможные ходы, допустимые в игре. Итак, мы находимся на некоторой площадке. Игрок, собирающийся сделать очередной ход, имеет возможность выбора любого хода (коридора лабиринта), допустимого в данной позиции. Если бы он видел лабиринт с высоты птичьего полета, то он мог бы наметить последовательность ходов, ведущую к матовой позиции или к ничьей. Но для человека это исключено. Он может мысленно экстраполировать развитие партии только на несколько ходов вперед, учитывая возможные ответные ходы противника. А это означает, что он может проанализировать лишь некоторую часть лабиринта, некоторую окрестность той площадки, где он сейчас находится. И он должен сделать выбор на основе этой локальной информации. Поэтому правила, которыми игрок руководствуется при выборе хода, неточны, эвристичны. Его выбор не обязательно приведет его к положению, которое приближает для него победу в игре. Он может допустить ошибку, чего-то не учесть вне анализируемой окрестности лабиринта. [c.19]
Мы вернемся к позиционной форме в гл. 2 (поскольку в этой главе нас интересуют стаические игры с полной информацией, для которых позиционная форма — это некоторое излишество), а теперь перейдем ко второй возможной форме представления игры — нормальной или стратегической форме, которая "суммирует" позиционную игру в трех элементах множестве игроков /, множестве стратегий каждого игрока и функции выигрышей, ставящей в соответствие каждому набору стратегий игроков соответствующие выигрыши игроков. [c.26]
Русский перевод статьи Куна см. сборник "Позиционные игры" (1967). Под ред. Н.Н.Воробьева и И. Н. Врублевской. М. Наука - Физматгиз. [c.89]
Предложение 4.2.1 (Kreps, Wilson (1982)j. В каждом последовательном равновесии (<т, //) позиционной игры ТЕ набор равновесных стратегий а образует совершенное под-игровое равновесие по Нэшу. [c.154]
Даже если большинство аналитиков сделают аналогичные прогнозы, вряд ли они одновременно и дружными рядами выйдут на рынок. Некоторые из них попытаются предвосхитить сигнал графика и вступят в игру как можно раньше. Другие начнут продавать или покупать на "прорыве" из определенной графической модели или идикатора. Третьи дождутся возвратного движения цен после прорыва, и только потом начнут действовать. Одни трейдеры более решительны и склонны к риску, другие более консервативны. Одни используют стоп-приказы, чтобы выйти на рынок, другие предпочитают рыночные или лимитированные приказы. Есть трейдеры, которых называют "позиционными", а есть "дневные" трейдеры. Таким образом, невозможно представить себе, что все трейдеры в определенный момент сыграют абсолютно одинаково. [c.25]
Я чувствую, что Вам нужно перескочить к завтрашней торговле, чтобы получить преимущество. Для меня преимущество, конечно, важно, однако не настолько, как исполнение. Но только с преимуществом Вы можете получить лучшее исполнение. Вы впереди игры, потому что Вы впереди дейтрейдеров, фондов, скальперов и позиционных трейдеров, так как Вы не пользуетесь их данными, следуя за ними. [c.50]
Формально позиционная форма игры описывается с помо- [c.86]
Определение 2.1.3. В игре в позиционной форме ГЕ стра- [c.94]
