Для решения задачи необходимо построить сетевой график строительно-монтажных работ. При построении графика проводятся процедуры, аналогичные описанным в упомянутой методике. Так как процесс строительства буровых хорошо отработан практически, то оптимизация сетевого графика по времени приводится к расчету минимальной продолжительности строительства, которая равна длине критического пути. После определения продолжительности строительства буровой требуется так разместить работы и людские ресурсы, чтобы потребление ресурсов было оптимальным. [c.98]
Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме. [c.114]
Резервы времени. Продолжительность критического пути больше продолжительности любого другого пути, следовательно, у некритических путей и лежащих на них работ и событий имеются резервы времени. При расчете сетевых графиков определяют резервы времени событии, полных путей, полные и свободные резервы времени работ [c.91]
Расчет сетевого графика по сетевой модели. Настоящая методика расчета сетевых графиков предусматривает расчет следующих параметров а) ранних сроков свершения событий 7> б) поздних сроков свершения событий Tf в) резерва времени свершения событий Tj n. [c.71]
| Рис. 4.6. Элемент сетевого графика при расчете по сетевой модели / — номер события 2,3,4 — соответственно ранний срок, поздний срок и резерв времени свершения события | 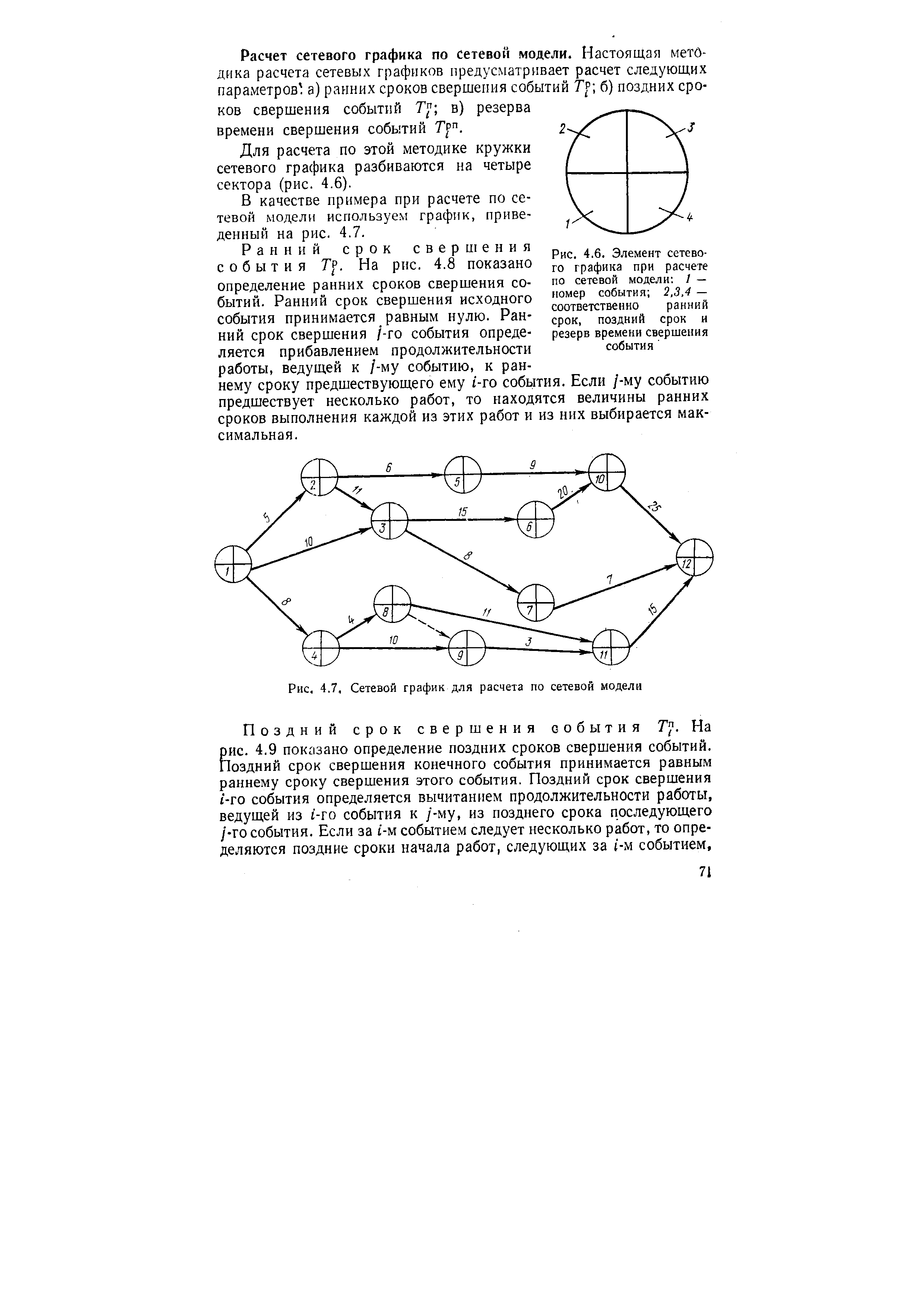 |
Построив сетевой график (сетевую модель- с определенными временными параметрами) и пронумеровав события, можно приступить к расчету сетевого графика. [c.20]
Шестой этап - расчет сетевого графика определение ранних и поздних сроков выполнения работ, резервов времени и критического пути. [c.50]
Полный список операций для дальнейшей обработки передается в вычислительную группу или обрабатывается на месте вручную. В процессе расчета определяются начало и окончание работ, критический путь и резервы времени с уточнением календарных дат. При расчетах сетевых графиков наибольшее распространение получили следующие обозначения [c.92]
В начале расчета сетевого графика определяются наиболее ранние и наиболее поздние сроки наступления отдельных событий. Расчет ведется от начального события 0 к конечному. В первую очередь определяются раннее начало и раннее окончание работ. Раннее начало работы определяется наибольшим временем из полученных при суммировании продолжительности отдельных операций на каждом из путей, ведущих от начального события к рассматриваемому. Например, для работы в пределах событий 5—6 (см. рис. 16) раннее начало составляет [c.92]
Иногда в сетевом графике может быть установлено несколько критических путей, длительность которых одинакова. Поиск критического пути, как правило, связан с определением резервов времени расчетом графика в обратном направлении от конечного события к начальному. [c.92]
Соответственно в оперативном центре управления на основании поступающей информации разрабатываются перфокарты для тех работ, по которым произошли изменения. В результате расчета на ЭВМ. определяются шифры объектов, попавших на критический путь, и количество дней, необходимых для полного завершения критических работ. Кроме того, по каждому объекту, включенному в сетевой график, уточняются продолжительность работ, их начало, свободный и полный запас времени в днях. Получив необходимые данные, оперативная группа производит соответствующие изменения к графике м сообщает результаты расчета ответственным исполнителям и руководителю комплекса работ. [c.97]
На рис. 5.2 дан пример сетевого графика, созданного для планирования сравнительно несложного комплекса работ. Над стрелками указано ожидаемое время выполнения работ. Этапы разработки и управления ходом работ с помощью сетевого графика имеют такую последовательность основных операций 1) составление перечня всех действий и промежуточных результатов (событий) при выполнении комплекса работ к графическое их отражение по типу, показанному на рис. 5.2 2) оценка времени выполнения каждого действия (работы), а затем расчеты сетевого графика для определения срока достижения поставленной цели 3) оптимизация рассчитанных сроков и необходимых затрат 4) оперативное управление ходом работ путем периодического анализа получаемой информации о выполнении заданий и выработки решений. [c.36]
Наиболее важная из проблем, которые приходится решать при осуществлении комплекса работ, — это распределение ресурсов между отдельными работами. Дело в том, что для проведения работ необходимо обеспечить их трудовыми и материальными ресурсами. Количество ресурсов различных типов, находящихся в распоряжении руководителя работ по проекту, обычно бывает ограничено. Очень часто этих ресурсов не хватает чтобы обеспечить завершение всех работ Рц в наиболее ранние моменты, которые равны ti + tij. В этом случае расчет резервов времени Мц и Мц для каждой работы позволяет определить, какие из работ PI/ должны получить ресурсы и быть начаты сразу после совершения предшествующих им событий (, а какие могут быть задержаны без ущерба для сроков осуществления проекта. Изложенные здесь соображения можно использовать как при предварительном планировании расписания выполнения работ, так и при оперативном управлении, когда ситуация с работами меняется, случаются задержки работ сверх полного резерва времени М] , что приводит к изменению критического пути и необходимости срочного перераспределения ресурсов между работами. Пересчет сетевого графика на ЭВМ, т. е. определение новых значений резервов времени, дает возможность быстро осуществить эту операцию. [c.190]
В ходе расчета сетевого графика определяются следующие параметры продолжительность работ и критического пути наиболее ранние и наиболее поздние сроки наступления событий и окончания работ все виды резервов времени для работ и событий, не лежащих на критическом пути. [c.110]
Резерв времени для событий показывает, на какой предельно допустимый период времени может задержаться свершение того или иного события, не вызывая при этом опасности срыва срока свершения конечного события. Если резерв события будет полностью использован, событие попадет на критический путь. Алгоритмы расчетов остальных параметров сетевого графика сведены в табл. VI.3. В том случае, если сроки выполнения всех работ не укладываются в директивные, необходимо произвести оптимизацию сети. В этих целях можно во-первых, увеличить количество исполнителей во-вторых, произвести перераспределение трудовых ресурсов путем переключения части работников с работ, имеющих большие резервы времени, на выполнение работ, лежащих на критическом пути. [c.111]
Построение сетевой модели в масштабе времени. Масштабный сетевой график строится на масштабной сетке времени.. Перед построением сетевого графика в масштабе времени необходимо произвести расчет его основных параметров. [c.114]
Критический путь и запасы времени определяются расчетом сетевого графика. [c.198]
Расчет сетевого графика производится в следующей последовательности. Для определения критического пути и запасов времени сетевой график просчитывается в прямом и обратном направлениях. Обсчет графика в прямом направлении определяет наиболее ранний из возможных сроков свершения события. Обсчет графика в обратном направлении определяет наиболее поздний из допустимых сроков свершения событий. [c.200]
Одним из важнейших понятий сетевых методов является понятие критического пути. Его определяют при расчете сетевого графика (сетевой модели). Критическим путем называется такая последовательность взаимосвязанных работ и событий, которая имеет наибольшую продолжительность во времени. Продолжительность критического пути характеризует и продолжительность всего комплекса работ в целом (на рис. 9.1 критическим является путь 1—4—5—6—9). [c.229]
Рассмотрим сетевой график на рис. 10.26. Продолжительность действий указана в неделях, также выделены критические действия. Расчеты резервов времени по этим действиям приведены в таблице ниже. [c.368]
Алгоритм анализа графа с возвратом основан на использовании метода статистических испытаний и известного алгоритма Форда для сетевых графиков. Процедура Форда используется для расчета временных параметров отдельных фрагментов графа с учетом их топологии и задаваемых характеристик, а методами Монте-Карло имитируется реализация соответствующих дуг возврата. Таким образом, центральной процедурой алгоритма является моделирование событий контроля и согласования методом статистических испытаний. Исходы этих событий описываются вероятностями повторного исполнения определенных фрагментов проекта. [c.197]
Если расчет сетевой модели показал временные затраты на выполнение задания (в данном < превышающие директивные, то проводится оптимизация сетевого графика по критерию времени в еле [c.99]
Расчеты резервов времени по действиям, отмеченных сетевом графике, изображенном на рисунке приведены в таблице 10 (приложение 5). [c.88]
Например, в рассмотренном ранее примере сетевого графика (рис. 20) общий резерв времени работы 2-5 по методу потенциалов равен (20 - 7) - (8 + 3) = 2, частный резерв этой работы -13 - (8 + 3) = 2. По работе 3-7 по методу потенциалов общий резерв равен (20 -4) - (10 + 2) = 4, частный резерв - 12 - (10 + 2) = 0, что совпадает с результатами секторного и табличного способов расчета. [c.91]
Наиболее часто в настоящее время применяются сетевые графики вида "работа-вершина" с постоянной продолжительностью работ. Для расчета временных показателей сетевых графиков в системах управления проектами применяют аппарат методов сетевого планирования и управления. [c.23]
Проведено обучение группы работников и руководителей проектов элементам сетевого планирования и управления (построение и расчет сетевых графиков, определение критического пути, ранних и поздних сроков, резервов времени операций). [c.459]
Объемно-календарный план инновационного проекта определяет продолжительность и объем работ, даты начала и окончания выполнения работ, тем и заданий проблемно-тематического плана, резервы времени и величины ресурсов, необходимых для реализации проекта. Цель календарных расчетов — регламентация согласованного хода работ с учетом целесообразной их последовательности и взаимосвязи по каждой теме (заданию) проблемно-тематического плана и по отдельным организациям-исполнителям (детальные календарные планы), а также по проекту в целом (сводный оптимальный календарный план). В качестве метода календарного планирования в системе управления инновационными проектами рекомендуется использовать методы сетевого планирования и управления (СПУ), получившие с начала 1960-х гг. широкое распространение в бывшем СССР. Система СПУ предусматривает детальное изучение будущих работ и представление их в виде специального чертежа — сетевого графика. Использование при календарном планировании проекта сетевых методов позволяет определить перечень наиболее ответственных работ, составляющих критический путь проекта установить минимальное время завершения проекта выделить работы, задачи с высоким риском выделить слишком интенсивные периоды деятельности. [c.116]
СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ (СПУ) —метод планирования и управления научно-исследовательскими и опытно-конструкторскими работами, строительством, технологической подготовкой производства и другими работами, в основе которого лежит использование сетевого графика как средства информации об управляемом объекте или процессе. Сетевой график отражает состав, связи и последовательность выполнения комплекса работ и событий, направленных на достижение конечного результата. Основными количественными оценками в СПУ являются время и затраты на выполнение работ. Важным для СПУ является понятие критического пути — комплекс работ и событий от начального до конечного события, имеющий наибольшую продолжительность. В процессе управления линейный руководитель постоянно контролирует работы и события, находящиеся на критическом пути (реализация принципа ведущего звена). Исходные оценки времени и затрат на выполнение каждой работы даются специалистами, выполняющими эти работы. Формальные процедуры формирования сетевого графика и расчета его параметров выполняет специальная [c.290]
Данные расчета временных параметров событий сетевых графиков необходимы также для целей планирования. [c.187]
Величину критического пути определяют по расчетной величине свершения заключительного события, а его структуру — по нулевым резервам работ. Так, в нашем примере длительность критического пути определилась равной 22 единицам времени (часов, минут) и на этом пути лежат следующие работы 0—/, /—3, 3—6, 6—7. На графике они отмечены жирной линией. При малых объемах сетевых графиков (40—70 событий) расчеты параметров могут быть проведены непосредственно на графике. Для этого метода расчета требуется некоторое увеличение фигур событий с делением их на 4 сектора (рис. 28). В верхнем секторе записывают номер события i, в левом — ранний срок наступления события ТРС[, а в правом — поздний срок наступления события ТПС[. К использованию нижнего сектора (четвертого) имеются различные подходы. Наиболее широко он используется для записи резервов события PI. [c.187]
После определения оценок времени по каждой работе проводится расчет сети. Каждая работа обычно требует затрат времени, труда, материалов, денежных средств. Поэтому сетевой график должен отразить сроки выполнения отдельных работ и всего комплекса, необходимые ресурсы рабочей силы и возможности маневрирования ею, затраты средств и др. [c.71]
В начале расчета сетевого графика определяем наиболее ранние и поздние сроки наступления отдельных событий. Расчет ведем от начального события О к конечному. В первую очередь определяем ранние начало < JJ и окончание tf—i работ. Раннее начало работы определяется наибольшим временем из полученных при суммировании продолжительности отдельных операций tt j на каждом из путей, ведущих от начального события к рассматриваемому. Для работы в пределах событий 5 — 6 (см. рис. 14) [c.93]
Когда кроме вычисляемого при расчете сетевого графика срока наступления завершающего события Тк (Тк = Тр= Т ) дается директивный срок Тд, минимальные резервы времени событий могут быть не равны нулю. При Гд > Тк минимальные резервы будут положительными, а при Гд < < Тк — отрицательными, тем не менее в обоих случаях именно мини-м 1льные или, как указывалось выше, нулевые резервы будут определять события, через которые проходит критический путь. [c.42]
Обратите внимание, что при методе действия в узлах не надо вводить псевдодействия. Это одна из причин того, почему подход действие в узле к составлению графиков проще, чем метод действие над стрелкой . Но трудности при дальнейшем анализе, в частности при расчете времени, приводят к тому, что многие обучаемые часто считают, что подход действие над стрелкой проще при решении вручную небольших задач, связанных с использованием сетевых графиков. [c.387]
Продолжительности начальных работ, по которым осуществляется стыковка сетевых графиков, приведены в табл. 14. Эти значения использованы в качестве периода запуска — выпуска при расчете стандарт-плана. В табл. 15 приведен пример стандарт-плана обработки деталей в цехе М-2 при стыковке сетевых графиков по начальным работам, продолжительности которых равны TI H = 100,00 тг i = =0,12 тз-4= 36,00 единицам времени. Аналогичные данные были рассчитаны для всех деталей, обрабатываемых в цехе М-2. [c.95]
Специализированная электромоделирующая установка АСОР-Г (рис. 3.6) предназначена для механизации расчетов сетевых графиков при планировании и управлении позволяет отражать топологию любого сетевого графика, определять конфигурацию и длину критического пути, а также следующие временные характеристики сети длину критического пути в целом и между событиями наиболее ранний возможный и наиболее поздний допустимый срок начала работы наиболее ранний возможный и наиболее поздний до- [c.134]
При расчете параметров сетевого графика предполагается, что работа над проектом начинается в момент времени, равный нулю. Это и есть ранний срок начала работ Ранний срок окончания каждой из первоначальных работ равен продолжительности их выполнения. Ранние сроки начала и окончания работ рассчитываются, начиная от исходного события и заканчивая завершающим событием. Ранний срок окончания работы равен продолжительности этой работы плюс ранний срок ее начала Для события, которому предшествуют несколько путей (на рис. П.5 —события 5, 6, 7, 8), ранний срок начала юследующей работы выбирается равным максимальному из ранних сроков окончания предшествующих работ На критическом пути ранний срок окончания работы, предшествующей завершающему событию, соответствует минимальной продолжительности работ над проектом и равен позднему сроку окончания этой работы. [c.223]
Основу сетевого графика составляют события и работы. Событие — это четко сформулированный момент начала или завершения одной или нескольких работ. Если событие является результатом нескольких работ, то оно считается совершившимся в момент окончания работы с наибольшей продолжительностью. На графике событие обозначают кружком (рис. 2), в котором проставляют его номер. При расчете сети- событие обозначают tf. Работа на сетевом графике означает операцию, процесс или совокупность процессов, требующих для своего совершения времени и ресурсов, а также ожидание, связанное с соблюдением определенных технологических перерывов. Работу на графике изображают сплошной стрелкой и обозначают номерами предшествующего и последующего событий tt j (где г — номер начального, а / — номер конечного события данной работы). Обозначение работы проставляют над стрелкой, а ее продолжительность в единицах времени — под стрелкой. [c.13]
Равномерное распределение можно использовать при расчетах по сетевым графикам работ, в том числе при работе по методу PERT. Это распределение можно применять и при расчетах основных длительностей и времен в военном деле (времени выдвижения воинской части или ее подразделения на исходный рубеж, времени марша, времени подготовки рубежа обороны и др.). [c.26]
Срок свершения 2-го, седьмого, двенадцатого, тринадцатого событий рассчитывается по максимальному из предшествующих ему путей. Срок свершения события 2 равен 10 дням (2+6+2), события 7—17 (2 + 6 + 2 + 7), события 12—18 (2+6 + 2 + 7+1), события 13—22(2+6 + 2 + 7+1+4). Значит, ранний срок свершения завершающего события — 22 дня, что соответствует величине, подсчитанной при определении полных путей и критического пути сетевого графика. В рассматриваемом сетевом графике поздний срок свершения последнего события 13 составляет 22 дня. Поздний срок свершения события 12 определяется вычитанием из позднего срока свершения события 13 продолжительности работы, ведущей от события 12 к событию 13, что составит 18 дней (22—4). Таким же образом устанавливаются поздние сроки свершения и всех остальных событий, кроме 1 и 9. После события 1 следует четыре работы работа 1—3, 1—2, 1—4, 1—5. В подобных случаях выбирается минимальная по продолжительности разность между поздним сроком свершения последующего события и сроком выполнения работы, ведущей от данного события к последующему. Отсюда поздний срок свершения события 1 составит 2 дня. Тп события 4 равен 8—22—(4 + 1+7+2). Принимаем срок в 2 дня, поскольку эта величина меньше возможных других трех величин, так как, если берем путь 1—3, то поздний срок свершения события 1 будет равен 22—(2 + 5 + 3+1)—4 = 7 дней, путь 1—2 —22—(4 + 1+7)—3 = 7дней, путь 1—5 22—(4 + 3 + 4 + +5)—2=4 дня. Аналогично этому ранний срок свершения события составит 22—(4 + 3-)—4 = 11 дней, так как, идя другим путем, величина Тп для события 9 будет больше 22—(4 + 1)—3 = = 14 дней. Разность между поздним и ранним сроками устанавливает резерв времени. Для события 1 резерв составит 0(2—2), для события 2 — также 0(10—10), для события 3—5 дней (11—6), события 4—0 (8—8), события 5—0 (4—4), события 6—5 дней (12—7), события 7—0(17—17), события 8—5 дней (15—10), события 9—2 дня (11—9), события 10—5 дней (20—15), события 11—2 дня (15—13), события 12—0 (18—18), события 13—0 (22—22). Так как критический путь проходит через события с нулевыми резервами времени, его продолжительность может быть определена как сумма времени свершения событий 1, 2, 4, 7, 12, 13, что совпадает с ранее сделанными расчетами длительности критического пути. [c.209]
