Случаи а) и б) представляют односторонние критические области, а случай в) — двустороннюю критическую область Рг — вероятность принятия гипотезы. [c.60]
Вероятность совершить ошибку первого рода принято обозначать через а, а вероятность совершить ошибку второго рода — через р. Для задачи статистического регулирования а называется риском излишней наладки, ар — риском незамеченной разладки. Критическими точками (границами) называют точки, отделяющие критическую область от интервала — области принятия гипотезы. Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области. Правосторонней называют критическую область, определяемую неравенством К>Ккр, где К — статистика критерия, Кщ, — положительное число (рис. 2.3). [c.25]
Для двусторонней критической области критическая точка МКР находится по таблице функции нормального распределения из условия [c.28]
Проверка гипотез при двусторонней критической области тесно связана с интервальным оцениванием. При одном и том же уровне значимости а и объеме выборки п попадание гипотетического значения исследуемого параметра в доверительный интервал равносильно попаданию соответствующего критерия в область принятия гипотезы. Поэтому для проверки гипотезы в этом случае можно использовать доверительный интервал. Если гипотетическое значение исследуемого параметра попадает в этот интервал, то делают вывод, что нет оснований для отклонения выдвигаемой гипотезы. Более подробно данная связь рассмотрена в примерах 3.2 - 3.8. [c.75]
Гипотеза в такой постановке обычно называется гипотезой о статистической значимости коэффициента регрессии. При этом, если Н0 принимается, то есть основания считать, что величина Y не зависит от X. В этом случае говорят, что коэффициент bi статистически незначим (он слишком близок к нулю). При отклонении HO коэффициент bi считается статистически значимым, что указывает на наличие определенной линейной зависимости между Y и X. В данном случае рассматривается двусторонняя критическая область, т. к. важным является именно отличие от нуля коэффициента регрессии, и он может быть как положительным, так и отрицательным. [c.121]
| Рисунок 15.7. Двусторонняя критическая область распределения Стьюдента | 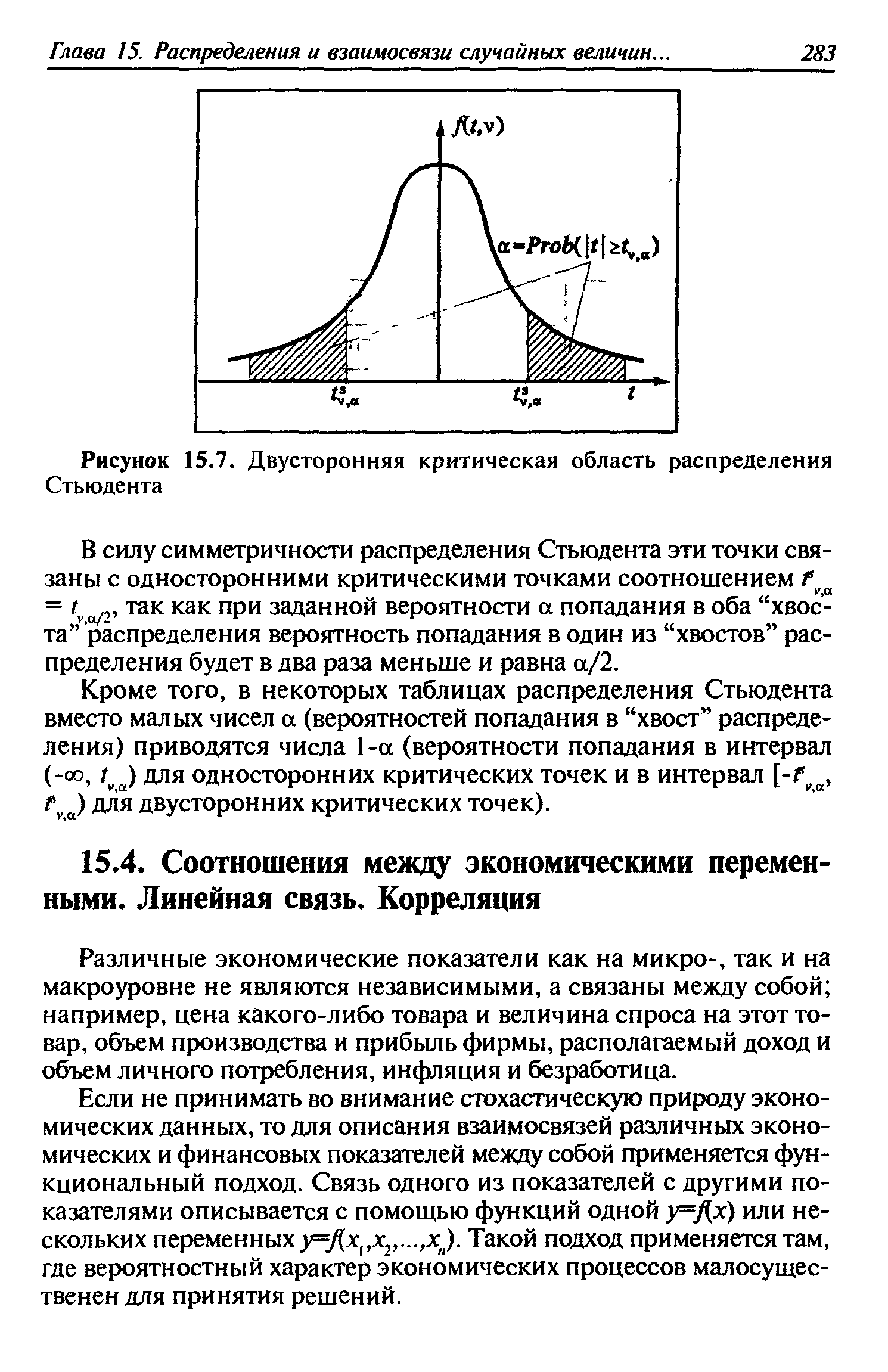 |
Площадь закрашенной области между и 1,88 равна 0,9699. Следовательно, площадь незакрашенной области справа от равна 0,9699 = Альтернативно, критическое значение которое отсекает область, площадь а = 0,05 и расположенную справа от критического значения, находится между 1,64 и 1,65 и равно 1,645. Обратите внимание, что при определении критического значения выборочной статистики область вправо от критического значения критерия равна либо а либо а/2. Это значение равно а для одностороннего критерия и а/2 — для двустороннего. [c.567]
При двусторонней проверке область справа от критического значения равна а/2 или 0,025. Следовательно, критическое значение тест-статистики равно Так как вычисленное значение чем критическое, нулевую гипотезу нельзя отклонить. Таким образом, различие в долях пользователей (0,733) для мужчин и (0,400) для женщин не считается статистически значимым. Обратите внимание, хотя различие довольно существенное, оно статистически незначимое из-за небольшого размера выборки (по 15 человек в каждой группе). [c.587]
Левосторонней называют критическую область, определяемую неравенством / Акр, где /(кр — отрицательное число (рис. 3.6,6). Двусторонней называют критическую область, определяемую неравенствами /С/Свф, где /t2KP>tfiKP. В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами К<Ккр, л>лкр равносильными неравенству К >ЛкР (рис. 2.3, в). [c.26]
Критическая область (-oo.)k1 6/2)u(k6/2,+oo) называется двусторонней критической областью. Она определяется в случае, когда альтернативная гипотеза имеет вид HI 0 Ф QQ. Кроме двусторонней, рассматривают также односторонние критические области - правостороннюю и левостороннюю. [c.74]
Можно показать, что в случае ограниченного интервала области при пятил гипотезы /70 (двусторонней критической области) существует связь интервала Д определяемого по (12 15), с доверительным пнтер-в,пом, определяемым по формуле (12.14). [c.228]
