Корреляционно-регрессионные методы анализа применяются для установления формы и тесноты связи между показателями. Целью анализа является получение аппроксимирующей функции [c.320]
Для определения основной тенденции развития явления во времени используют различные аналитические функции. С помощью математических методов подбирается такое уравнение тренда, которое максимально точно отображает изменение показателя во времени и обеспечивает близость значений эмпирических и выравненных данных. На практике чаще всего используют следующие аппроксимирующие функции [c.612]
Для того чтобы получить максимально точный результат аналитического выравнивания эмпирических данных, характеризующих уровень процентных ставок, строят несколько трендовых моделей с применением различных аппроксимирующих функций. Далее, фактические и теоретические данные наносят на график и получают информацию о том, какая из выбранных функций наиболее реально отражает общую тенденцию развития исследуемого показателя. [c.613]
Выявление основной тенденции осуществляется подбором наилучшей аппроксимирующей функции, которая, как правило, не должна иметь -обратную формулу. (Это проявление циклических колебаний.) Современные пакеты прикладных программ предлагают выбор (в том числе автоматический) около 16 функций. Как правило, вековой тренд неплохо отражает прямая. График выравнивания курса доллара к марке по прямой линии (у = 1,6853 — 0,004 t) приведен на рис. 15.3. Исходными данными послужили среднемесячные курсы за апрель 1987 г. — ноябрь 1996 г. (по данным аген- [c.662]
Далее, для нахождения аналитической формы приведенной зависимости и коэффициентов действуют следующим образом (что и является главной особенностью методики). Изучают тип связи и подбор аппроксимирующих функций зависимости прироста спроса и предложения от валютного курса отдельно по данным растущего курса и падающего (графа 7 и графа 6 табл. 15.1). [c.677]
При правильно определенной аппроксимирующей функции ф(х, bo, b, ..., bp) с увеличением объема выборки (л-юо) она будет сходиться по вероятности к функции регрессии ф(х). [c.52]
С целью обеспечения возможности использования функции желательности для оценки параметров различной размерности и порядка производится приведение параметров изделия Pt к значениям приведенного параметра х функции желательности/ Для этого по известным значениям х и / на границах интервалов функции желательности строится аппроксимирующая функция и определяются ее параметры (коэффициенты). Наиболее простая — это линейная функция вида [c.30]
В этот момент функция Q(t.) должна быть заменена другой аппроксимирующей функцией Q,(t.), вид и параметры которой определяются по данным текущих измерений и уточняются по мере поступления новых данных. При достижении заранее заданной точности аппроксимации (т.е. когда достоверность факта развивающегося дефекта установлена) производится расчет оптимального времени начала ремонтных мероприятий. [c.129]
Анализ динамики снижения дебитов после проявления дефекта оборудования позволил установить, что функция Q,(t.) является выпуклой, т.е. d2Q/dt2 <0, что указывает на увеличение темпов развития дефекта. Простейшей, и в большинстве случаев достаточно точной аппроксимирующей функцией оказалась квадратичная зависимость [c.129]
Практическое осуществление предлагаемого алгоритма состоит в следующем. На основании ретроспективного анализа дебитов конкретной конденсатной скважины методом наименьших квадратов вычисляются коэффициенты линейной аппроксимирующей функции Q(t), а также дисперсия О2[ ] случайной составляющей. При поступлении новых данных по дебиту скважины производится вычисление вероятности принадлежности текущего замера Q. временному [c.129]
В построении таких характеристик в настоящее время нет неразрешимых проблем. Тем более эта задача облегчается по мере ввода в практику нефтеснабжения автоматизированных систем сбора и переработки информации, благодаря чему информацию, собираемую для целей оперативного контроля, можно накапливать и, использовать в построении аппроксимирующих функций случайных величин и определении статистических характеристик процессов [19]. [c.257]
Однако построение аппроксимирующих функций распределения путем проверки приемлемости различных статистических гипотез без предварительного анализа природы случайного процесса может дать далеко не лучшее приближение к реальным условиям, особенно, если речь идет об использовании этих распределений для прогнозирования. [c.258]
Для выбора аппроксимирующих функций необходимо возможно более детальное представление о закономерностях рассматриваемого случайного процесса и формирование обоснованных гипотез о его характере. [c.258]
Для этого по известным значениям х и Р на границах интервалов функции желательности строится аппроксимирующая функция, и определяются ее параметры (коэффициенты). [c.46]
По полученным значениям рассчитаем параметры аппроксимирующих функций. Достаточно достоверное приближение дает степенная функция третьего порядка вида/= а-х3 + Ь-х2 + с-х + d. Ее коэффициенты для каждого из признаков приведены в таблице A3. [c.89]
Этот график дает основания предположить, что связь переменных X и Y носит периодический характер. По методике, изложенной в предыдущих 2-х параграфах, представим аппроксимирующую функцию рядом Фурье и построим амплитудно-частотную характеристику. [c.135]
D - суммы модулей отклонений аппроксимирующей функции от [c.49]
Аппроксимация — замена одних математических объектов другими, в том или ином смысле близкими к исходным. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов. Например, для приближения заданной функции/(д ,) выбирают аппроксимирующую функцию Ф(х) из классов математических функций, в наибольшей степени соответствующих специфике протекания исследуемого процесса. [c.25]
Формальная экстраполяция сводится к математически оптимальной подгонке исходного статистического ряда к какой-либо аппроксимирующей функции. Критерием оптимальности здесь может выступать близость точек ряда к аппроксимирующей функции. [c.25]
В качестве аппроксимирующих функций применяются не только линейная (выравнивание по прямой линии), но и квадратическая, параболическая, экспоненциальная и др. Пример выравнивания динамического ряда по прямой см. на рис. М.2, где сумма квадратов расстояний - у j)2 + (y2-у 2)2.... — наименьшая, и получившаяся прямая наилучшим образом отражает тенденцию динамического ряда наблюдений за некоторым показателем во времени. [c.196]
Очевидно, что сильное обобщенное решение одновременно является и слабым. Для доказательства достаточно записать формулу интегрирования по частям для произвольной гладкой в Р функции у и фигурирующих в определении 4.4.2 аппроксимирующих функций yk [c.339]
Подбор функции, описывающей аналитическую зависимость страховой составляющей нормы производственного запаса от уровня надежности обеспечения им, осуществляется путем аппроксимации полученного выше ряда (двенадцати пар значений) и определения по этой функции стандартных табличных значений. Стандартные уровни надежности обеспечения производственным запасом у = 60 61 62 63 . .., 99 99,7% в общем случае лежат внутри диапазона полученных ранее табличных значений изменения у, рассчитанных по формуле (6.50), и не всегда в них есть данные результаты. Для полученных табличных данных Еи - f(j), состоящих из 40 пар значений (Еи, уи), нужно подобрать одну (две или три) аппроксимирующую функцию, которая наилучшим образом описывала бы аналитически эту зависимость во всем рассматриваемом диапазоне изменения страхового запаса. При этом результаты расчетов по ней значений страховых составляющих нормы производственного запаса должны мало отличаться от табличных значений (имели наименьшее среднеквадратическое отклонение). Это позволит вычислить страховые составляющие нормы производственного запаса для стандартных уровней надежности (например, для уровня 90 или 99,7%), которых может и не быть в полученных выше данных, а будут близкие к ним, одни табличные данные будут больше указанных конкретных значений, другие — меньше. [c.321]
В данной работе мы будем рассматривать две задачи оптимальной оценки и идентификации. Как видно из предыдущих рассуждений, эти задачи существенно различаются как по постановке, так и по интерпретации результатов. Действительно, если целью является получение различных интерполяционных формул или исследование связи для изучения возможностей интерполяции, содержательная интерпретация результатов нас не интересует. Например, не играет никакой роли с профессиональной точки зрения выбор вида аппроксимирующей функции. Единственным [c.17]
Аппроксимирующая функция График плат-тат вероятности. , [c.90]
| Рис. 5.1. Взаимное расположение истинной, теоретической аппроксимирующей и выборочной аппроксимирующей функций регрессии в примере 5.1 | 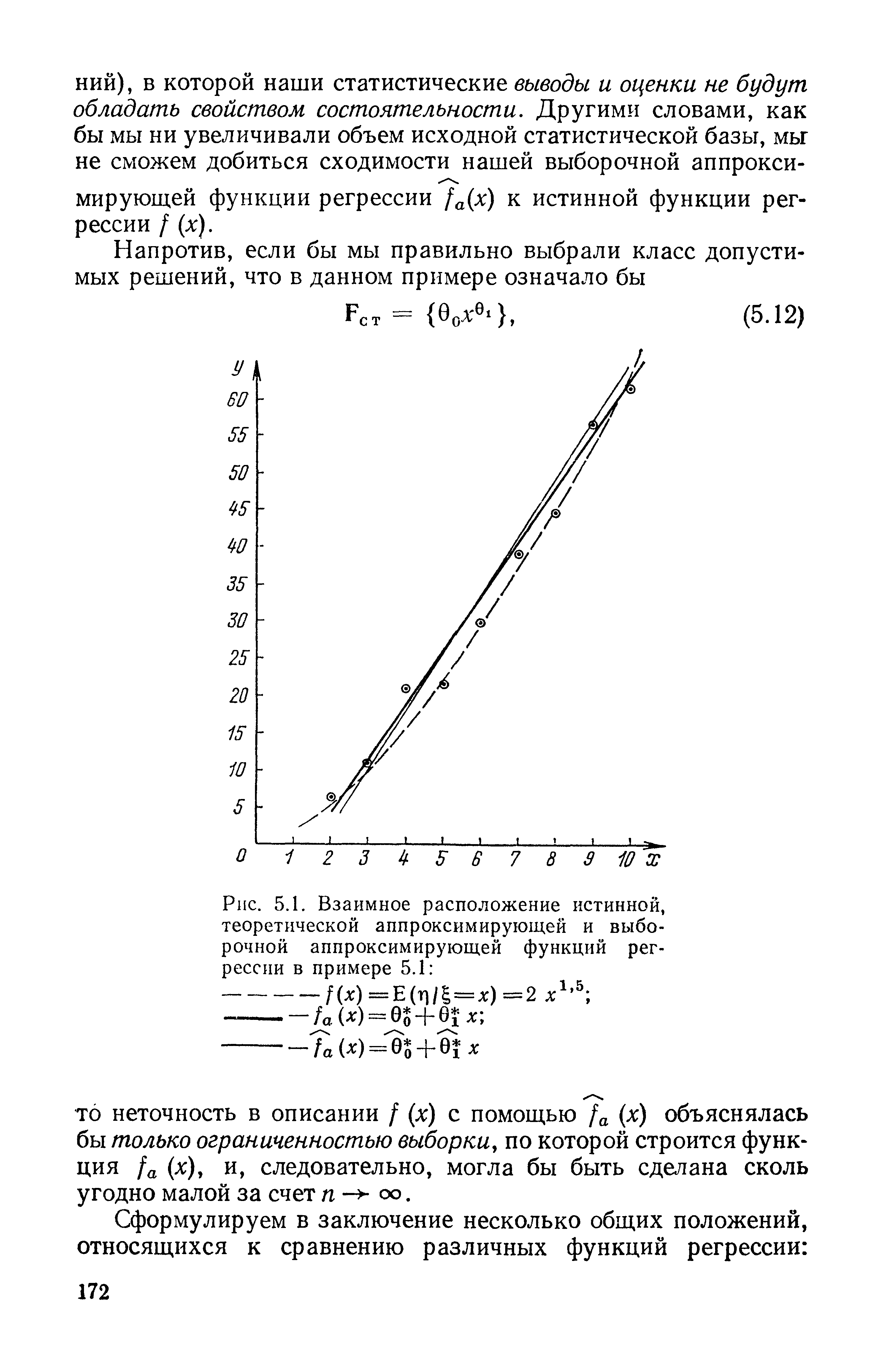 |
Сплайны сравнительно мало известны прикладным статистикам. Вместе с тем, по мнению ряда авторов [54, 114], они являются наиболее удачными аппроксимирующими функциями для приложений. Дело здесь в том, что поведение функции, выражающей физические взаимоотношения, в одной области пространства может быть полностью. не связанным с ее поведением в другой области. Полиномы наряду с большинством других математических функций обладают как раз обратным свойством. Их поведение в малой области однозначно определяет поведение в любой другой точке. Сплайны, поскольку они определяются кусочно, лишены этого недостатка, и для [c.328]
Для равноотстоящих на единицу масштаба узлов базисные сплайны В0> Blt B2, B3 показаны на рис. 10.2. 10.3.2. Выбор порядка сплайна, числа и положения узлов. Это важная и ответственная задача, по своей методической роли эквивалентная выбору класса аппроксимирующих функций в обычном регрессионном анализе. От ее успешного решения существенно зависит, удастся ли при анализе данных использовать все преимущества, представляемые сплайнами, или нет. Здесь трудно дать рекомендации, верные для всех практических задач. Однако, следуя [2581, мы попытаемся вы- [c.330]
Допустим, что известна средняя задержка в очереди к ресурсу tqt. Тогда можно аппроксимировать функцию распределения времени пребывания в очереди hq, t) выражением [c.51]
Отождествление сущности связи с формой (типом функции) ее описания ведет иногда к эмпиризму, подтасовке эмпирического материала к заранее разработанным теоретическим гипотезам и выдаче результатов подобного эмпирического анализа в качестве доказательства теоретических выводов. В качестве формы связи в литературе приводят статистические функции, которые наиболее точно описывают данные эмпирических наблюдений. Соответственно говорят о линейной, квадратичной,гиперболической, экспоненциальной и т. п. формах связи, хотя имеется в виду лишь форма аппроксимирующей функции. [c.118]
Непосредственное прогнозирование параметров развития науки и телники методом экстраполяции производится по рассчитанным аппроксимирующим функциям. Для этого выбирают требуемое значение аргумента периода прогнозирования, лежащее за пределами эмпирических данных, вводят его в полученное уравнение и рассчитывают ожидаемое значение прогнозируемого параметра в будущем. [c.112]
В прогнозной модели, используемой IEA для прогнозирования развития мирового рынка энергоносителей (таблица 4.3), предполагается, что страны — производители ресурсов имеют некоторый заданный тренд потребления энергии в отличие от стран-потребителей, потребности которых моделируются системой некоторых динамических уравнений. Это более совершенная модель, чем WEPS, однако имеющая свои ограничения, связанные в основном с выбором аппроксимирующих функций. Основной формулой является модельная функция стоимости поставки ресурсов (например, газа) [c.70]
Соотношение истинной (/ (X)), теоретической аппроксимирующей (fa (X)) и выборочной аппроксимирующей (fa (X)) регрессий существенно зависит от выбора критерия адекватности Д (fa) (определяемого природой регрессионных остатков е) и класса допустимых решений F. В частности, даже при удачном выборе критерия адекватности Д в ситуациях, когда истинная функция регрессии / (X) не накрывается классом допустимых решений F (т. е. когда / (X) Ё F), выборочная аппроксимирующая функция регрессии fa (X) не будет стремиться к истинной при неограниченном росте объема выборки (отсутствие свойства состоятельности у fa (X), объясняемое неустранимостью ошибки аппроксимации). [c.174]
| Рис. 13.1. Прямые 1, 2 и 3 — графики аппроксимирующих функций регрессии, построенных соответственно по наблюдениям подвыборок 1 (точки), 2 (крестики) и по объединенной выборке, состоящей из тех и других наблюдений | 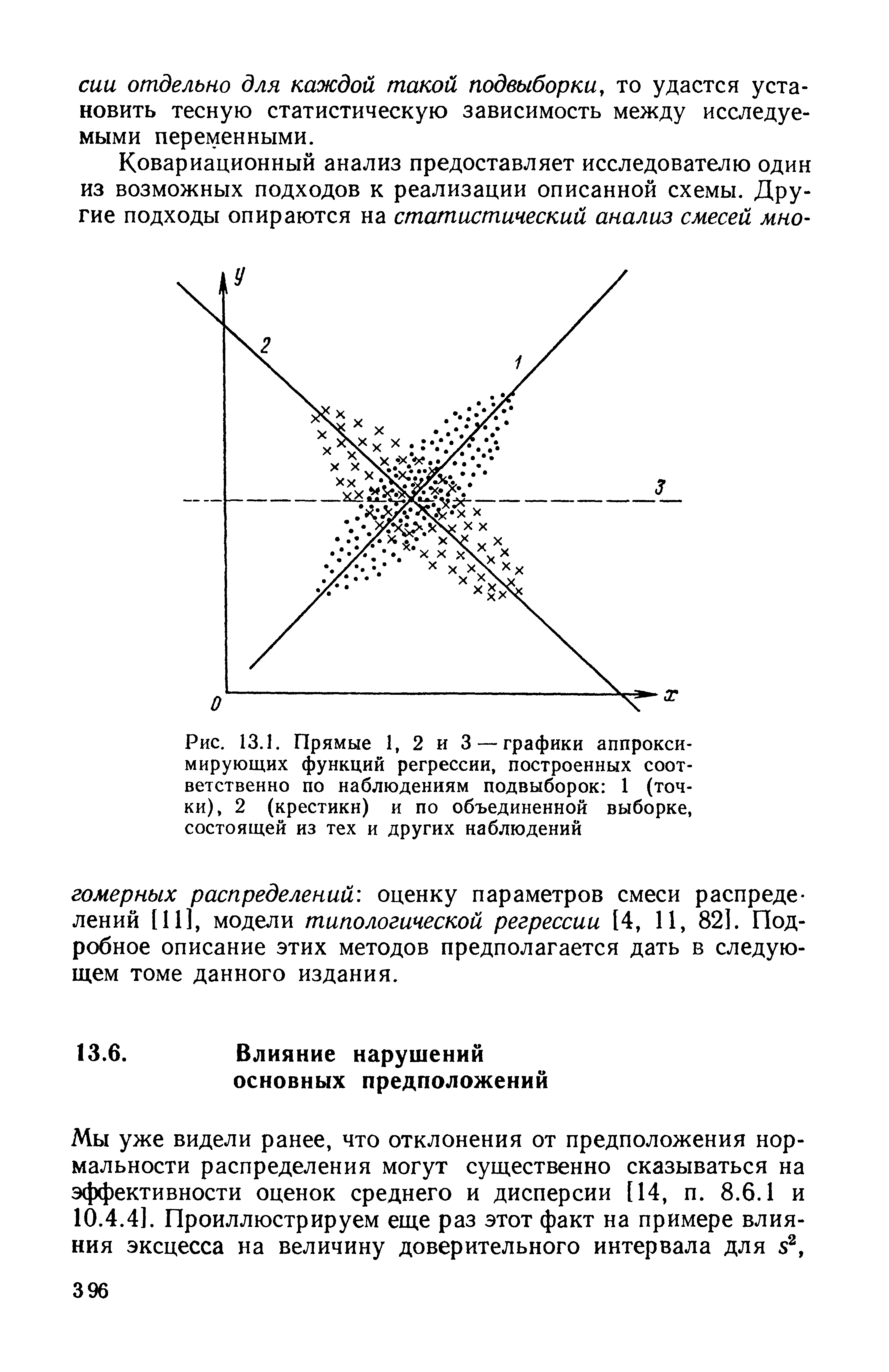 |
