Понятие об авторегрессионных моделях и моделях скользящей средней [c.146]
Авторегрессионная модель р-го порядка (или модель AR (р)) имеет вид [c.147]
Если исследуемый процесс у, в момент t определяется его значениями только в предшествующий период t — 1, то рассматривают авторегрессионную модель 1-го порядка (или модель AR (1) — марковский случайный процесс). [c.147]
Используя авторегрессионную модель 1-го порядка, дать точечный и интервальный прогноз среднего и индивидуального значений курса акций в момент t= 23, т. е. на глубину один интервал. [c.147]
В соответствии с условием применим авторегрессионную модель (6.12). Получим (аналогично примеру 6.2) [c.148]
Заметим, что уравнение (7.31) является авторегрессионным уравнением первого порядка (см. 6.5). [c.174]
Рассмотрим авторегрессионную зависимость остатков от их предыдущих значений, используя авторегрессионную модель р-то порядка AR(p). Применяя метод наименьших квадратов, получим следующее уравнение [c.175]
Наиболее распространенным приемом устранения автокорреляции во временных рядах является подбор соответствующей модели — авторегрессионной AR(p), скользящей средней MA(q) или [c.178]
Полезную информацию можно получить с помощью выборочных, автокорреляционной и частной автокорреляционной функций. В самом деле, вспомним, что выборочная частная автокорреляционная функция л,аст(р) есть оценка параметра рр в авторегрессионной модели р-то порядка. Отсюда делаем вывод [c.179]
Авторегрессионная модель первого порядка [c.181]
В большинстве компьютерных пакетов реализованы также итеративные процедуры, позволяющие оценивать значение параметра модели (7.34) при условии, что остатки модели образуют стационарный временной ряд, моделируемый как авторегрессионный процесс первого порядка, т. е. автокорреляция имеет характер (7.35). [c.185]
Считается, что ошибки регрессии представляют собой стационарный авторегрессионный процесс первого порядка. Можно ли сделать вывод, что коэффициент Я. а) больше 0,5 б) больше 0,7 Объем выборки достаточно велик. [c.222]
Третий путь прогноза — использование авторегрессионных схем, базирующихся на зависимости значении показателя в будущей временной точке от его значения в предшествующей, равноотстоящей от нее. Естественно, что народный доход n-го года тесно связан с величиной этого показателя в предшествующем (п—1)-ом и в (п—2) -ом году. Благодаря огромной инерции, которой обладает народное хозяйство, параметры, характеризующие динамический ряд синтетического показателя, существенно не меняются для двух близлежащих периодов, как можно видеть из сравнения уравнений парабол 2-го порядка, вычисленных для 1950—1964 гг. [86], 1950— 1965 гг., 1950—1966 гг. и 1950—1967 гг. (табл. 11) [c.157]
Ту же близость параметров при некотором удлинении исходного ряда можно отметить и по другим типам кривых. Это логически ведет к попытке искать улучшения прогноза на пути построения авторегрессионных уравнений (исходный ряд из табл. 9, гр. 2). [c.157]
Мы построили для рассматриваемого нами показателя — глобального народного дохода — четыре авторегрессионных уравнения, отражающих 1) зависимость народного дохода данного года (yi) от народного дохода предшествующего года (yt-i) 2) зависимость этого же показателя от его значения в предшествующем году и от времени 3) зависимость его же от объема народного [c.157]
| Рис. 7. Авторегрессионная схема динамики глобального народного дохода в фактических ценах, в 1950—1967 гг. (в млрд. руб.) | 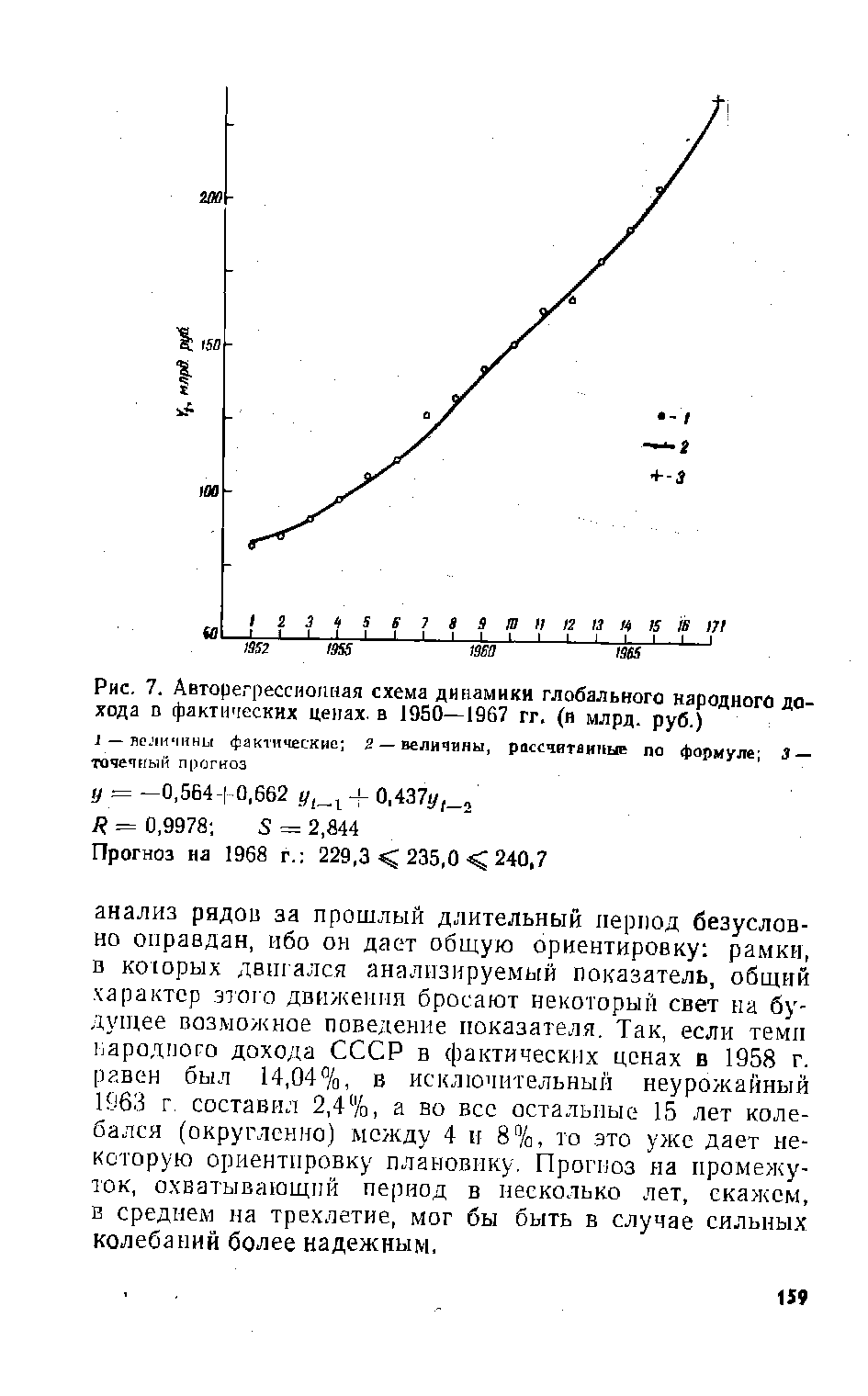 |
В табл. 19.6 сравнивается точность четырех прогнозов. Первый прогноз, обозначенный RW, — это ежегодный прогноз, сделанный на основе модели, напоминающей модель случайных колебаний (см. уравнение (19.16)). Второй прогноз, обозначенный AR, — это ежегодный прогноз на основе авторегрессионной модели, которая похожа на модель из уравнения (19.19). Третий прогноз — это средний прогноз, опубликованный I/B/E/S, и четвертый — это последний прогноз, публикуемый I/B/E/S. [c.615]
Установите зависимость между следующими данными о квартальной прибыли, используя авторегрессионную модель первого порядка (используйте рекомендованную компьютерную регрессионную модель). Каков ваш прогноз уровня прибыли в 21-м квартале [c.623]
Квартальные прибыли как авторегрессионный процесс [c.1002]
Учесть указанные выше сложности позволяет также построение в рамках метода главных компонент авторегрессионной модели. Например, для отражения совокупного движения prime-rate краткосрочных операций США, ставок ТВ США, разницы в процентных ставках США и Японии, ставок краткосрочных операций Японии и курса иены и доллара была разработана следующая авторегрессионная модель (13) [c.672]
Глава 8 посвящена рассмотрению стохастических регрессо-ров и использованию специальных методов инструментальных переменных. Здесь же дано описание специальных моделей временных рядов (авторегрессионных, скользящей средней, с распределенными лагами и их модификаций), позволяющих наиболее эффективно решать задачи анализа и прогнозирования временных рядов. [c.4]
Наряду с авторегрессионными моделями временных рядов в эконометрике рассматриваются также модели скользящей средней1, в которой моделируемая величина задается линейной функцией от возмущений (ошибок) в предыдущие моменты времени. [c.148]
В заключение этой главы отметим, что использование соответствующих авторегрессионных моделей для прогнозирования экономических показателей, т. е. автопрогноз на базе рассмотренных моделей, может оказаться весьма эффективным (как правило, в краткосрочной перспективе). [c.149]
Если ряд стационарный, то, как можно доказать, выборочный частный коэффициент корреляции гЧЯС1(р) совпадает с оценкой обычного метода наименьших квадратов коэффициента рр в авторегрессионной модели AR(p) [c.175]
Если удастся построить АКМ4-модель для ряда остатков, то можно получить эффективные оценки параметра р, а также несмещенные и состоятельные оценки дисперсий р с помощью обобщенного метода наименьших квадратов. Мы рассмотрим эту процедуру на простейшей (и в то же время наиболее часто встречающейся) авторегрессионной модели первого порядка. [c.181]
ADL — от английских слов autogressive distributed lags . Следует отметить, что наряду с авторегрессионной моделью ADL(p,q) в эконометрике используется и обычная регрессионная модель с распределенными лагами р-ro порядка (или модель DL(p)) [c.200]
Авторегрессии модель проинтегрированной скользящей средней ARIMA (p, q, k) 221 Авторегрессионная модель 135, 146 [c.299]
Цацулин А.Н. Построение авторегрессионных схем анализа и прогноза в условиях очень малых выборок // Сб. Научные труды ЛИСТа им. Ф. Энгельса, вып. 65. — Л. ЛИСТ, 1977. — ее. 84—91. [c.432]
Авторегрессионное уравнение (1950-1987 гг. в млрд. руб.) Среднее квадрати-ние, а Коэффи-irr на 1968 г. [c.158]
Гемиктери В. И., Френкель А. А. Прогнозирование случайных процессов с помощью авторегрессионных моделей.—Заводская лаборатория, 1967, № 7, с. 853—858. [c.227]
Серьезная депрессия по типу 1920-21 годов - маловероятна. Мы не наблюдаем длительную ликвидацию". Это был анализ, предложенный своим подписчикам через день после крушения Гарвардским Экономическим Обществом. После непрерывных и ошибочных оптимистических прогнозов, общество закрылось в 1932. Таким образом, два наиболее известных экономических института прогнозов в Америке не сумели предсказать вовремя приближающийся крах и депрессию и продолжали излагать оптимистические прогнозы будущего даже тогда, когда Великая Депрессия охватила Америку. Причина проста предсказание разворотов тренда представляет намного более трудную задачу для предсказателей и такие предсказания очень ненадежны, особенно в рамках линейной структуры стандартных (авторегрессионых) экономических моделей. [c.28]
В таком контексте мы предсказывали приблизительный рост рынка на 50% в течение последующих 12-ти месяцев, начиная с января 1999 года, допуская, что индекс Nikkei останется в пределах допустимого уровня ошибки соответствия. Предсказания изменений тренда исключительно сложны и ненадежны, особенно в линейной структуре авторегрессионых моделей, используемых в стандартных экономических анализах. Представляемая нелинейная структура хорошо приспособлена для прогнозирования изменений трендов, что ставит перед предсказателями куда более сложную задачу. Здесь мы рассматриваем наше предсказание изменения тренда в жестких рамках уравнения (25) тренды - это ограниченные периоды времени, характеризующиеся монотонным осцилляторным поведением, показанным на Рис. 155. Изменение тренда, таким образом, представляет собой пересечение локального минимума или максимума осцилляции. При помощи нашей формулы, кажется, удалось предсказать два изменения тренда, медвежьего на бычий в начале 1999 года и бычьего на медвежий в начале 2000 года. [c.333]
