Контрольные карты различаются по назначению. Они могут применяться для регулирования настройки производственного процесса (карты средних арифметических значений и медиан) и для регулирования рассеяния показателей качества (карты средних квадратических отклонений, размахов, вариаций), для оценки стабильности процессов (карты кумулятивных сумм). [c.159]
Чаще всего применяют карту средних арифметических значений и выборочных средних квадратических отклонений (карта х/а ). В ней помещаются отдельные графики средних арифметических значений х и выборочных средних квадратических отклонений G. Границы регулирования параметра с устанавливаются расчетом по формуле [c.163]
Как. известно, распределение характеризуется определенными параметрами средней арифметической, размахом вариации, сред-не-квадратическим отклонением. [c.150]
Первые четыре строчки в табл. 27 (средние значения, их ошибки, средние квадратические отклонения, коэффициенты вариации) вычислены по, всей исходной информации объединения за 1956—1970 гг. Остальные (чистые коэффициенты корреляции, автокорреляционные отношения Неймана, дифференциальные производительности и эластичности факторов) получены на базе кинетической функции (49) при средних величинах себестоимости добычи нефти и попутного газа и факторов. Среднее арифметическое значение уровня себестоимости и факторов достаточно высоки (первая строка, табл. 27). Стандартные ошибки средних значений свидетельствуют о небольшом различии между генеральными и выборочными средними значениями, что повышает статистическую достоверность последних. [c.91]
Среднеквадратическое отклонение (о) характеризует абсолютное отклонение индивидуальных значений от средней арифметической и рассчитывается по алгоритму [c.75]
Относительную меру отклонений от средней арифметической, или коэффициент вариации (V), определяют по формуле [c.75]
Среднее квадратическое отклонение показывает среднее отклонение значений варьирующего признака относительно центра распределения, в данном случае средней арифметической. Этот показатель рассчитывается по формуле [c.84]
Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа. [c.84]
Чтобы правильно применять средние величины, следует знать, от каких причин зависит различие между простой и взвешенной средними. Рассмотрим этот вопрос на примере арифметической средней. Пусть х - простая средняя, xz - взвешенная средняя, в которой весами выступают значения признака z, n - число единиц совокупности. Отклонения индивидуальных значений признака х, от простой средней х обозначим Д = дс,. - х. Отклонения признака-веса А2, = г, — г". Тогда индивидуальные значения признаков х и z можно выразить через их средние и отклонения х, = х + А,, г, = I + Аа, а взвешенную среднюю х2 представить в виде [c.85]
Так как суммы отклонений индивидуальных значений признака от средней арифметической согласно первому ее свойству равны нулю, то второе и третье слагаемые числителя также равны нулю. [c.85]
По данным табл. 5.6 средний модуль, или среднее линейное отклонение, по абсолютной величине вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины, т.е. по формуле [c.105]
Для дальнейшего изучения характера вариации используются средние значения разных степеней отклонений отдельных величин признака от его средней арифметической величины. Эти показатели получили название центральных моментов распределения порядка, соответствующего степени, в которую возводятся отклонения (табл. 5.7), или просто моментов (нецентральные моменты используются редко и здесь не будут рассматриваться). Величина третьего момента ц, зависит, как и его знак, от преобладания положительных кубов отклонений над отрицательными кубами либо наоборот. При нормаль- [c.109]
Следовательно, кривая нормального распределения может быть построена по двум параметрам - средней арифметической ц, и среднему квадратическому отклонению а. [c.197]
Для анализа полученных значений обычно используют коэффициент вариации. Он представляет собой отношение СКО к средней арифметической (среднему ожидаемому значению) и показывает степень отклонения полученных значений [c.41]
Метод, основанный на вычислении средней арифметической, или просто средней, обычно считается наиболее приемлемым. Он очевиден просто сложите имеющиеся значения и поделите сумму на их количество. Все просто, в том числе отработка данных таблиц частот. Однако, несмотря на всю эту простоту, зачастую этот метод наименее адекватен. Рассмотрим распределение заработной платы на рис. 1.17. Данная диаграмма иллюстрирует типичное распределение доходов всех работников крупной организации. Это положительно асимметричное распределение, с областью больших отклонений в правой части диаграммы. Доходы основной массы работников представлены в левой части диаграммы. Только несколько работников имеют доходы, представленные у верхней границы диаграммы. Вот эти-то несколько работников и искажают значение средней, и усредненное значение, полученное путем расчета арифметической средней, превышает приемлемо репрезентативное значение. Значение моды соответствует максимальному значению частот, представленных в распределении. При такой форме распределения это значение находится в области нижних значений заработной платы и поэтому также не является полностью репрезентативным. Значение медианы, как центральное значение, выступает в роли компромиссного решения и часто считается наилучшим показателем. На рис. 1.17 представлены значения средней, моды и медианы. Эти три показателя будут находиться в соответствии друг с другом, только если распределение данных симметрично. Если распределение отрицательно асимметрично, тогда последовательность значений меняется на обратную. Так, средняя будет наименьшим значением, а мода — наибольшим. На рис. 1.18 представлены три типа распределения с соответствующими показателями трех средних . Рисунки просто отображают форму каждого распределения. Так, проведенные кривые очерчивают контуры соответствующей гистограммы. Например, на рис. 1.18 (i) отображена форма, представляющая такое же распределение, что мы видим и на рис. 1.17. [c.30]
Количество сверхурочных часов - это переменная, обозначаемая х, для которой мы хотим найти значение среднеквадратического отклонения. Сначала находим среднюю арифметическую [c.38]
Средняя арифметическая и среднеквадратическое отклонение по этим данным можно получить, сведя последние в таблицу, как это показано ниже. Количество единиц товарных запасов есть рассматриваемая переменная, обозначаемая х, а количество дней есть соответствующая частота, обозначаемая / Сначала рассчитываем среднюю арифметическую (х) по формуле A/Z/- Затем получаем остающиеся три колонки значений. [c.39]
Вычисления средней арифметической и среднеквадратического отклонения сведены в следующую таблицу [c.40]
Значения средней арифметической, приведенные в таблице, показывают, что средняя заработная плата в электронной отрасли выше, чем в строительной. Таким образом, в целом работники электронной отрасли зарабатывают больше, чем работники строительной отрасли. Однако в строительной отрасли выше значение среднеквадратического отклонения. Это указывает на то, что в стро- [c.41]
Среднеквадратическое отклонение , . Коэффициент вариации = -------Среднее арифметическое-------- х 100 [c.46]
D) Рассчитайте среднюю арифметическую и среднеквадратическое отклонение на основании следующих наборов данных [c.50]
Найдите среднюю арифметическую и среднеквадратическое отклонение возраста зрителей этих двух программ. Прокомментируйте различия в возрасте между двумя группами и по возможности объясните их. [c.51]
Нормальное распределение является одним из наиболее важных видов распределения вероятностей, используемых при принятии управленческих решений. Этот вид распределения можно обнаружить во многих практических примерах, и он особенно ценен при рассмотрении выборок из большой совокупности. Нормальное распределение, представленное на рис. 2.11, — симметричное, колоколообразное и может быть полностью определено значениями средней арифметической и среднеквадратического отклонения. Средняя арифметическая (ц) определяет центр распределения, а среднеквадратическое отклонение (ст) определяет его разброс. На рис. 2.12 показано, как разница в значениях средней арифметической влияет на положение графика, а на рис. 2.13 показано, как увеличение значения среднеквадратического отклонения меняет размах кривой. Однако, несмотря на изменение значений арифметической средней и среднеквадратического отклонения, базовая форма нормального распределения, определенная нормальной кривой, сохраняется. [c.78]
Определение участков под нормальной кривой требует сложной математической формулы. Данный процесс упрощается при использовании особых таблиц. Обычно это таблицы стандартного нормального распределения , где средняя арифметическая равна 0, а среднеквадратическое отклонение — 1. Любое нормальное распределение с заданной средней арифметической (ц) и заданным среднеквадратическим отклонением (а) можно привести к этому стандартизованному распределению с помощью следующей формулы [c.79]
Значение z, определяемое по данной формуле, дает расстояние между значением (х) и средней арифметической (ц), выраженной относительно количества среднеквадратических отклонений. [c.79]
| Рис. 2.14. Нормальная кривая, средняя арифметическая = 200, среднеквадратическое отклонение = 50 | 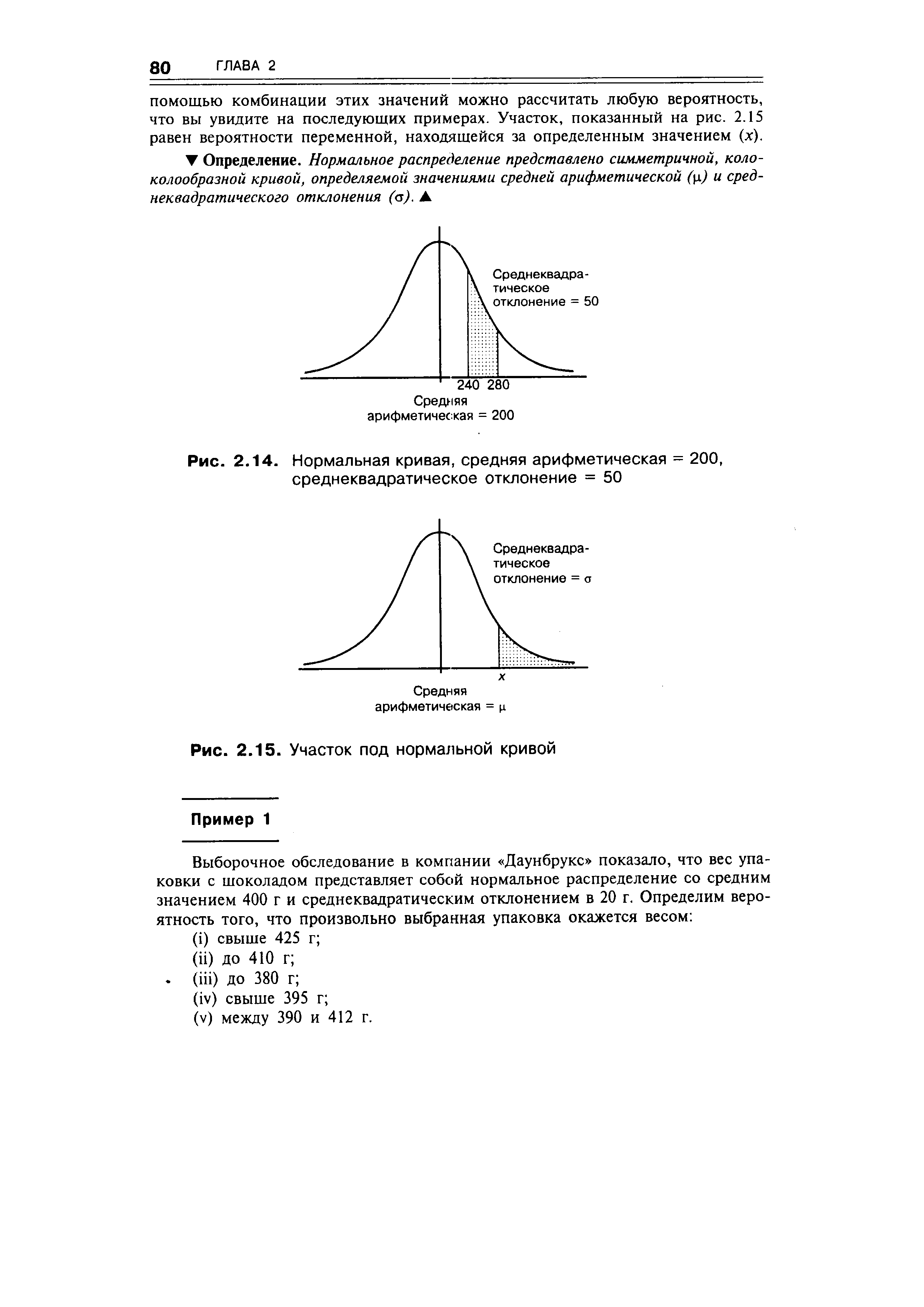 |
I) Установлено, что количество пациентов, поступающих еженедельно на лечение в клинику Св. Иосифа, представляет собой нормальное распределение со средней арифметической в 400 пациентов и среднеквадратическим отклонением в 90 пациентов, [c.85]
Рассмотрим задачу определения количества коек, необходимого в специализированном отделении клиники Св. Иосифа. Общее количество ежедневно необходимых коек представляет собой нормальное распределение со средней арифметической в 60 и среднеквадратическим отклонением в 10. Руководство хочет быть в достаточной степени уверено, что имеется необходимое число коек для удовлетворения ежедневных потребностей. Фактически руководство установило, что количество имеющихся коек должно быть достаточным, по крайней мере, на 99 дней из каждых 100. [c.85]
Т Определение. Если выборки объемом п взяты из совокупности со средней арифметической ц и среднеквадратическим отклонением а, то распределение выборочных средних имеет среднюю арифметическую ц и среднеквадратическое отклонение r/V/j. A [c.88]
Примечание. Xt, X,-- себестоимость и факторы функции m,-, S,-— среднее арифметическое значение г-того фактора и средней ошибки а , V — средние квадрати-ческие отклонения и коэффициент вариации i-того признака г/ — частный коэффициент корреляции i-того фактора У,-, Э — предельная производительность и эластичность г-того фактора. [c.96]
Номер переменной Средне-арифметическое значение Средне-квадратиче-ское отклонение Вариация, % Асимметрия Эксцесс Ошибка [c.142]
Итак, средняя арифметическая взвешенная равна простой средней плюс произведение среднего квадратического отклонения ос-редняемого признака на коэффициент вариации весового признака и на коэффициент корреляции между этими признаками. Если обе части равенства (5.5) разделить на простую среднюю х, получим [c.86]
Как мы уже говорили в предыдущем разделе, вероятности могут быть путем определения участка под кривой. Итак, общая площадь пространства под любой нормальной кривой равна общей вероятности (= 1). Рассмотрим нормальную кривую со средней арифметической, равной 200, и сред неквад рати -ческим отклонением, равным 50. Это распределение представлено на рис. 2.14, а вероятность нахождения значения в пределах между 240 и 280 показана затемненным участком. [c.79]
Т Определение. Нормальное распределение представлено симметричной, коло-колообразной кривой, определяемой значениями средней арифметической ( л) и сред-неквадратического отклонения (а). А [c.80]
Рассмотрим совокупность упаковок с шоколадом весом 400 г производства компании Даунбрукс . Вся продукция имеет среднюю арифметическую 400 г и среднеквадратическое отклонение 20 г. Каждый час из произведенной продукции отбираются и взвешиваются по 25 упаковок, а затем фиксируется выборочное среднее. Эту информацию можно использовать для определения распределения этих выборочных средних. Мы знаем среднее совокупности ц = 400 и среднеквадратическое отклонение совокупности а = 20, а также объем выборок п = 25. [c.88]
Известно, что дневная выработка трюфелей Труфл представляет собой нормальное распределение со средней арифметической 2500 изделий и средне-квадратическим отклонением 300 изделий в день. После запуска новой установки на производстве в течение 50 дней проводилось выборочное обследование, в ходе которого была зафиксирована среднедневная выработка в 2600 изделий. Начальник производственного отдела считает, что это свидетельство того, что запуск новой установки привел к увеличению выработки. Чтобы проверить данное утверждение, рассмотрим распределение выборочных средних и попробуем установить, насколько сильно изменилось новое значение среднего. [c.89]
В компании Даунбрукс полагают, что средний вес определенного шоколадного изделия составляет 400 г. Известно, что среднеквадратическое отклонение при этом равно 20 г. На линии выборочно обследовали 100 изделий и установили, что среднее арифметическое составляет 402 г. Проверим, опровергает ли данное обследование предположение о средней совокупности. [c.90]
