Напомним, что эластичность является локальной характеристикой функции ее значения изменяются при переходе от одного значения аргумента к другому (или от одной комбинации аргументов, если их несколько, к другой). При обсуждении затрат длительного периода мы рассматривали как типичный [/-образный характер изменения средних затрат. При малых значениях q функция АС убывала, затем проходила свое минимальное значение, а при больших q — возрастала. Это означает, что малым значениям q отвечают значения [ТС] < 1, при больших — имеет место неравенство [ГС] > 1. Эффективному размеру фирмы соответствует минимум АС, т. е. такой объем производства, при котором [ТС] = 1. [c.641]
| Рис. 8A.2. Средние переменные затраты как среднее значение функции общих переменных затрат. | 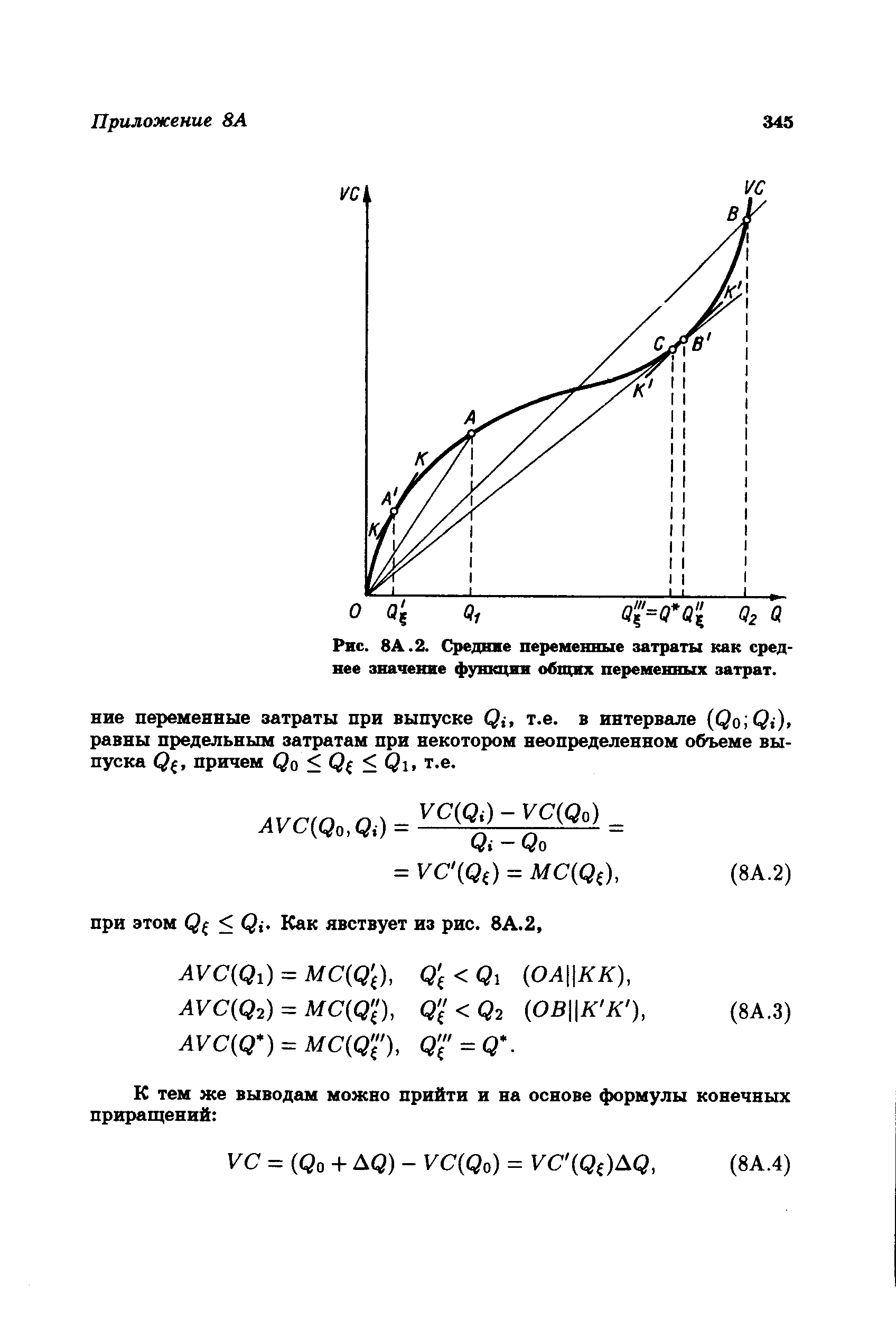 |
| Рис. 8А.З. Средние общие затраты как среднее значение функции общих затрат. | 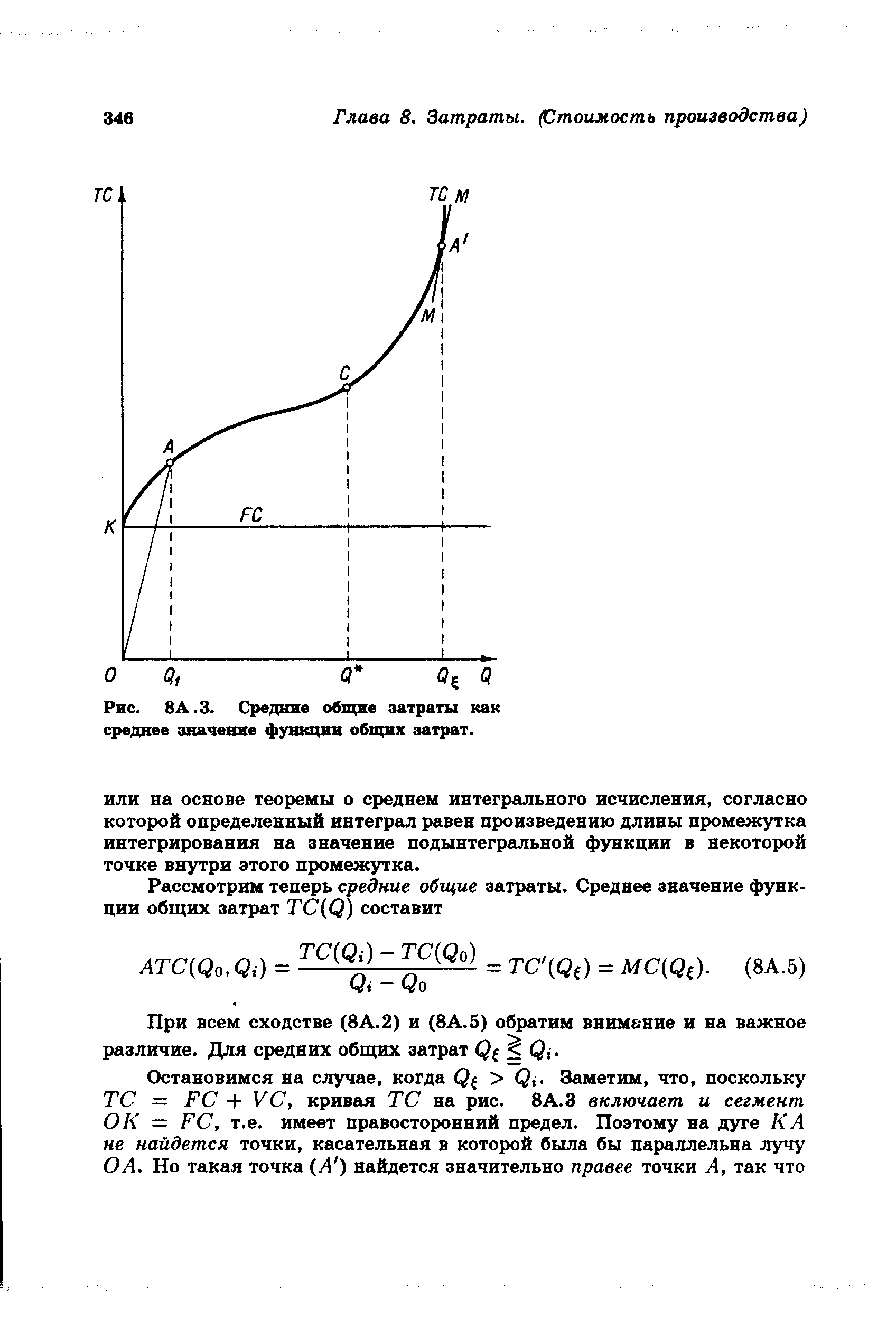 |
Функция спроса (средней выручки). Предполагается, что наш гипотетический продукт таков, что спрос на него равен нулю при цене р, большей или равной 21. Функция спроса дискретна (так же как функция затрат). Величина спроса определяется только для целочисленных значений р. График функции спроса начали строить от точки с координатами р = 21,д = 0и затем вычисляли прирост спроса, соответствующий пошаговому сокращению цены. Приращения выбирались одним из двух методов 14 1) в сериях 1-5 приращения однородно распределяются по целым числам 1,. .., 64 2) в серии 6 приращение t составляет Xt + 2t, где Xt однородно распределяется по целым числам 1,. .., 64. Заметим, что функция общей выручки не должна быть везде вогнутой и что при цене, равной нулю, величина спроса конечна. [c.457]
Кроме научно обоснованного распределения дохода между структурными единицами отделения, для эффективности арендного подряда важное значение имеет правильный выбор формы его организации, при этом должна быть учтена специфика деятельности соответствующего структурного подразделения. Так, для депо можно рекомендовать арендные взаимоотношения, аналогичные тем, которые складываются на промышленных предприятиях между администрацией этого предприятия и коллективами его цехов, производств, т. е. основанные на выдаче подрядного задания. Такая же схема может быть рекомендована для пассажирских и товарных станций, локомотивных депо и т. п. Для обслуживающих структурных единиц, например, службы связи, диспетчерские и т. п., наиболее приемлемой формой арендного подряда должна стать абонементная. При этой форме на основе статистических данных за ряд лет и их экономического анализа определяется оптимальная стоимость абонемента, включающая в себя право на затраты (по плану) и рентабельность (исходя из среднего по отделению норматива). Предметом договора в данном случае является качественное и бесперебойное выполнение соответствующих функций. Уменьшение или увеличение дохода (прибыли) может произойти как за счет более или менее экономного расходования всех видов ресурсов на содержание службы, так и за счет разницы в суммах уплаченных и полученных хозрасчетных санкции за несоблюдение сторонами, заключившими договор, его условий (сроки, качество и т. п.). [c.131]
Гибра [98] разработал модель определения оптимальных параметров контрольных карт средних арифметических значений. Этими параметрами являлись объем выборки, период отбора выборок и коэффициенты для определения положения границ регулирования. Примечательно, что рассматриваемая модель контрольных карт используется не только для обнаружения разладки, но и как основа для предписаний по управлению качеством продукции. Последнее очень важно, потому что приемлемость продукции создается при проектировании контрольных карт и будет зависеть по меньшей мере от результатов текущих измерений показателей качества продукции. Очевидно, что применение контрольных карт для приемочных процедур требует замены функции затрат на обнаружение разладки функцией затрат на приемочный контроль. Автор предполагает, что стандартное отклонение остается неизменным и процесс подвержен разладке по одной причине н одной переменной. [c.134]
Кривая АС отражает непрерывную тенденцию только в том случае, если предположить, что масштаб завода можно изменять небольшими приращениями. Если интерпретировать эту кривую как разрывную, то значимыми на ней будут лишь точки N, NI, N2,..., а значимые затраты в длительном периоде для интервалов между этими точками будут представлять собой минимальные из имеющихся средние затраты в коротком периоде для указанных объемов выпуска. На графике видно, что в определенных точках кривые ас для короткого периода проходят ниже кривой АС для длительного периода. Если считать, что кривая А С имеет значение только в точках N, это останется без последствий, но если считать, что кривая АС — непрерывная функция, это приведет к ошибке. Согласно моим указаниям, кривую АС должны были построить таким образом, чтобы она ни на одном участке не проходила выше кривой ас. Поскольку кривую строил математик, а не экономист, он приводил какие-то математические аргументы против такого построения. Эти возражения мне были непонятны, но я не смог заставить его пренебречь ими и выполнить мои указания, какими бы абсурдными они ему не представлялись. [c.114]
Методы 3-5 включают линейные функции спроса и линейные, квадратичные и логарифмические функции затрат соответственно. Так как функция общих затрат порождается по существу так же, как и функция спроса, она является псевдолинейной (за исключением серий 4 и 5, где она псевдоквадратичная), и мы на основании предыдущих аргументов ожидали от метода 3 наилучших результатов в сериях 1-3 и 6. Если учитывать среднюю прибыль, это оказалось не совсем так, однако по любому критерию сложно провести различие между эффективностью методов 3 и 5. Три этих метода дают высокую среднюю прибыль, методы 3 и 5 обеспечивают наибольший результат в сериях 1-3 и 6. В сериях 4 и 5 функция затрат псевдоквадратичная, а метод 4 дал лучшие показатели средней прибыли, как и должно было быть. По другим критериям они тоже дают вполне хорошие результаты. За исключением метода 6 — по данным методов 3-5 — значения прибыли показывают наименьшие стандартные отклонения, в большинстве случаев меньшие, чем стандартные отклонения численных значений подлинной оптимальной прибыли. В большинстве случаев (кроме серии 3, метод 4) стандартное отклонение, деленное на среднюю прибыль, дает тот же порядок значений для методов 3-5, как для максимальных значений прибыли. Стандартное отклонение разности между средней и максимальной прибылью является наименьшим (за одним незначительным исключением) для методов 3-5 и изменяется от серии к серии таким образом, что препятствует однозначной оценке [c.468]
В заключение можно упомянуть, что эффективность указанных эмпирических методов в получении средней прибыли просто замечательна, если учесть, что вычисления прибыли основывались на функциях спроса и затрат, построенных только по паре точек. Так как кривые спроса и затрат являются псевдолинейными или псевдоквадратичными в описанном смысле, резонно было бы ожидать хорошего приближения к подлинным функциям, когда исходные точки лежат относительно далеко друг от друга. Однако мы ожидали довольно слабого приближения, когда точки лежат близко друг к другу. Поэтому в целом показатели средней прибыли (являющиеся средними значениями хороших и плохих оценок) удивительно хороши далее в серии 3. Хотя взятые как процентное отношение к максимальной прибыли показатели методов значительно ухудшились в серии 3 (например, метод 3 дал в среднем в этой серии лишь 55.3% максимальной прибыли), абсолютное расхождение между максимальной прибылью и средней прибылью осталось по существу неизменным в трех сериях разница между показателями максимальных прибылей и прибылей по методу 3 составила 417.31 в серии 1, 512.09 в серии 2 и 599.70 в серии 3. [c.469]
Пусть мы хотим сделать выбор между двумя способами производства в условиях неопределенности относительно требуемого объема производства. Затраты по способу 1 даются функцией a- -bx, a по способу 2 — функцией v- -wx, где х — объем производства. Предположим, что a
Переход от этой матрицы ресурсов к таблице-матрице Маккелви (см. рис. 4) можно произвести, исходя из следующих соображений. В приведенной формуле степень потенциальной разведанности ресурсов г является косвенным измерителем риска их освоения — ресурсы меньшей степени изученности более рискованные, поэтому предполагается, что функция г(г () отражает рост затрат в связи с повышением степени неопределенности при переходе к менее разведанным ресурсам. Соответственно вместо функции г(6Д отражающей рост затрат на повышение КНИ, можно рассматривать функцию затрат от набора параметров, выражаемых многомерным вектором X (включающим такие параметры, как глубина залегания, удаленность, степень развития производственной и социальной инфраструктуры и т. д.) для некоторого среднего значения КНИ =/( ). [c.30]
Смотреть страницы где упоминается термин Средние затраты как среднее значение функции
: [c.155] [c.208] [c.210] [c.135]Смотреть главы в:
Микроэкономика Том 1 -> Средние затраты как среднее значение функции
