Биноминальная модель

Биноминальная модель оценки стоимости опциона  [c.651]

Если надо узнать, чему равна внутренняя (действительная) стоимость опциона в момент времени 0, то для ответа на этот вопрос используется биноминальная модель оценки стоимости опциона.  [c.651]


Чтобы воспроизвести опцион колл в условиях биноминальной модели, необходимо купить h акций [где h - коэффициент хеджирования из уравнения (20.5)]. Одновременно необходимо получить под ставку без риска средства путем короткой продажи облигации. Эта сумма равна  [c.655]

Биноминальная модель оценки премии опциона может использоваться для определения действительной стоимости опциона при предположении, что базисный актив будет равен одной из двух возможных известных цен по истечении каждого из ограниченного числа периодов и при условии, что известна его цена в начале каждого периода.  [c.678]

Биноминальная модель оценки стоимости опциона первоначально была разработана в книге  [c.687]

Более подробно о теории биноминальных моделей см. в статье  [c.688]

Так как в развитии бизнеса предполагается, что возможны два результата, то для определения стоимости опциона на отказ возможно применение биноминальной модели, которую разработали У. Шарп, Д. Кокс, С. Росс и М. Рубинштейн [64].  [c.332]


Уравнение однопериодной биноминальной модели ценообразования европейских опционных контрактов put на акции, не выплачивающие дивиденды, имеет вид  [c.332]

Уравнение двухпериодной биноминальной модели оценки опционных контрактов имеет вид  [c.333]

Многопериодная биноминальная модель оценки опционных контрактов представляется выражением  [c.334]

Использование биноминальной модели при разбиении временного интервала, оставшегося до исполнения опциона, на 5 периодов дает результаты, приблизительно совпадающие с результатами расчета по формуле Блэка-Шоулза.  [c.285]

Методы, основанные на Биноминальной Модели (В-М)  [c.190]

Дискретное время — методы на основе биноминальной модели (В-М)  [c.198]

ПРОСТАЯ БИНОМИНАЛЬНАЯ МОДЕЛЬ ОЦЕНКИ  [c.155]

Используем рассмотренный принцип для оценки премии опциона применительно к простой биноминальной модели, то есть модели, когда значение опциона и курса акций рассматривается только в начале и конце некоторого периода времени Т. Предположим, выписывается европейский опцион колл на 5 месяцев с ценой исполнения 36 долл. В момент заключения контракта цена акций равна 33 долл. Непрерывно начисляемая ставка без риска 10%. На основе своих расчетов инвестор определил, что курс акций к моменту истечения контракта может составить 34 долл. или 38 долл. Необходимо оценить премию опциона.  [c.156]

БИНОМИНАЛЬНАЯ МОДЕЛЬ ДЛЯ АКЦИЙ, НЕ ВЫПЛАЧИВАЮЩИХ ДИВИДЕНДЫ  [c.157]

Биноминальная модель основывается на концепции формирования портфеля без риска. Поэтому для дисконтирования принимается процент, равный ставке без риска для инвестиций, соответствующих времени действии опционного контракта. Для того, чтобы упростить модель, вместо указанной выше ставки используем эквивалентную ей ставку непрерывно начисляемого процента.  [c.159]


Мы рассмотрели биноминальную модель оценки премии опциона для акций, не выплачивающих дивиденды. В нашем примере весь период опционного контракта, который насчитывал три месяца, был разбит на три периода. На практике для определения цены опциона период Т необходимо разбить на большее число периодов At. Обычно деление опционного контракта на 30-50 интервалов дает приемлемый результат.  [c.163]

Как уже было отмечено в начале данной главы, биноминальная модель используется для оценки премии американских опционов. Премии европейских опционов рассчитываются с помощью аналитических формул, которые мы рассмотрим в следующем параграфе.  [c.166]

Премию американских опционов рассчитывают с помощью биноминальной модели. Суть ее состоит в том, что время опционного контракта разбивают на малые интервалы и строят с учетом вероятности дерево распределения курсовой стоимости акции. Определив премию опциона перед датой истечения контракта, последовательным дисконтированием под ставку без риска находят значение цены опциона для каждой точки пересечения дерева распределения и таким образом рассчитывают величину премии в момент заключения контракта. Если в период действия опциона на акцию выплачиваются дивиденды, то при 1) наличии информации о ставке дивиденда курсовую стоимость акции в момент выплаты дохода уменьшают на величину ставки дивиденда 2) когда имеются данные об абсолютной величине дивиденда, чистую стоимость акции для каждого узла дерева распределения корректируют на приведенную стоимость дивиденда.  [c.175]

Траектории биноминальной модели изображены на рис. 1.30. Если случайный процесс j5(w,t) является биномиальной моделью с параметрами u, d, р, то  [c.91]

Операции с опционами. Биноминальная модель. Формула Блэка-Шоулеса. Портфель с опционами, его риск и доходность. Репликатный портфель.  [c.86]

Рис. 20.5. Биноминальная модель оценки стоимости акций компании Widget 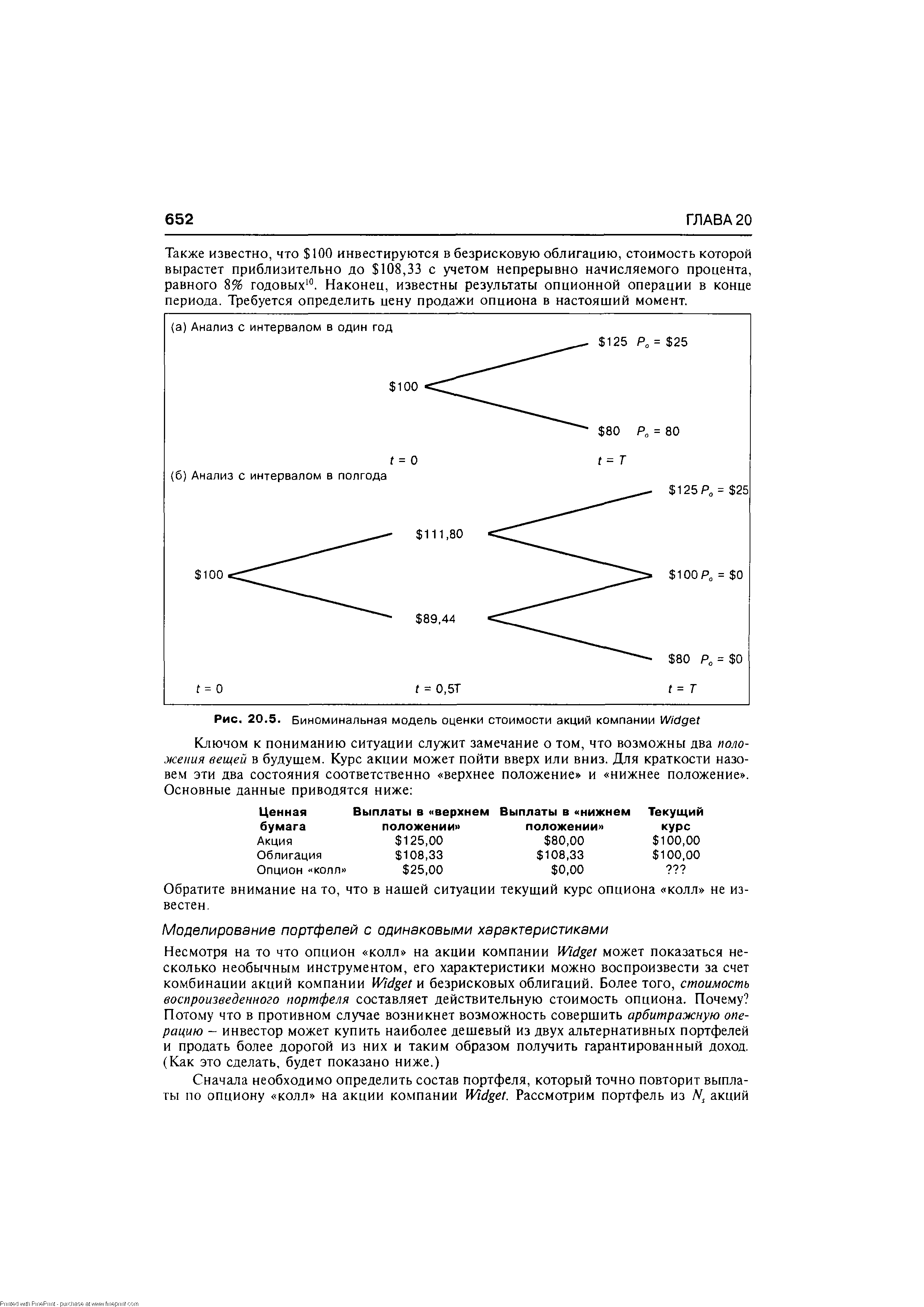Рис. 20.5. Биноминальная модель <a href="/info/114925">оценки стоимости акций</a> компании Widget
Настоящая глава посвящена проблеме определения премии опционных контрактов. Вначале мы остановимся на общем теоретическом подходе к расчету цены опциона, рассмотрим вопрос формирования портфеля без риска и оценки величины премии с помощью простой биноминальной модели. После этого перейдем к моделям, которые используются на практике, а именно, биноминальной модели и модели Блэка-Сколеса для акций, выплачивающих и не выплачивающих дивиденды. В рамках модели Блэка-Сколеса остановимся на таких вопросах, как логнормаль-ное распределение и стандартное отклонение цены актива.  [c.154]

Оценка премии европейских опционов на индексы, фьючерсные контракты, облигации и валюту, а также американских опционов колл в случае, когда их досрочное исполнение не является оптимальной стратегией, осуществляется с помощью формул Блэ-ка-Сколеса. Премии американских опционов рассчитываются на основе биноминальной модели.  [c.182]

В 1994 г. Дерман и Кани разработали модель, базирующуюся на биноминальном дереве, ранее использовавшуюся для долгосрочных американских опционов на акции, для оценки барьерных опционов в условиях кривой волатильностей (каждому периоду соответствует свой уровень волатильности). Постепенно биноминальные модели эволюционировали в триноминальные, дав возможность более точной оценки премий опционов.  [c.148]

Это означает, что ожидаемая доходность инвестиции в базисные рискованные активы совпадает с безрисковой процентной ставкой, если в исходной одноэтапной биноминальной модели вероятность подъема цены активов равна тг. Следовательно, if можно интерпретировать, как вероятность подъема цены базисных активов в мире, нейтральном к риску (risk-neutral world). В этом случае равенство (2.43) можно переписать в следующем виде  [c.153]