Типичными примерами матриц, которые могут быть применены для этих целей в нефтеснабжении являются [c.373]
Построение цифровой модели календарного плана при параллельно-последовательном выполнении смежных операций показывается в табл. 42 на примере матрицы времени 3-го случая (табл. 39) II варианта очередности запуска деталей. [c.169]
Последовательное преобразование матрицы А(0) применительно к данному примеру (матрицы а, б, в, г) показано ниже. [c.95]
В табл. 31 приведен пример матрицы РАФУ, построенной по приведенной выше методике. [c.121]
О = 1, m), на пересечении строк и столбцов проставляются количественные оценки показателей. Пример матрицы исходных данных представлен в таблице 2.51. [c.274]
| Таблица 3.6. Пример матрицы отчетности для проекта-примера |  |
X Этап П. Определяем рациональный порядок объезда пунктов каждого маршрута. Для этого строим таблицу-матрицу (табл. 4.15), в которой по диагонали размещаем пункты, включаемые в маршрут, и начальный пункт А, а в соответствующих клетках — кратчайшие расстояния между ними. Для примера матрица принята симметричной Q = Сп, хотя приведенный ниже способ [c.145]
Уравнение (4.4), а также упражнение 5.15.1 утверждают, что у невырожденных матриц ранг локально постоянен. Вырожденные матрицы (точнее, матрицы с рангом, меньшим полного по строкам или столбцам) этим свойством не обладают. Рассмотрим, к примеру, матрицы [c.202]
Особенности выбора наилучшей стратегии лучше всего уяснить на примере матрицы (25) [c.108]
| Рис. 39 ПРИМЕР МАТРИЦЫ БАЛЛОВ | 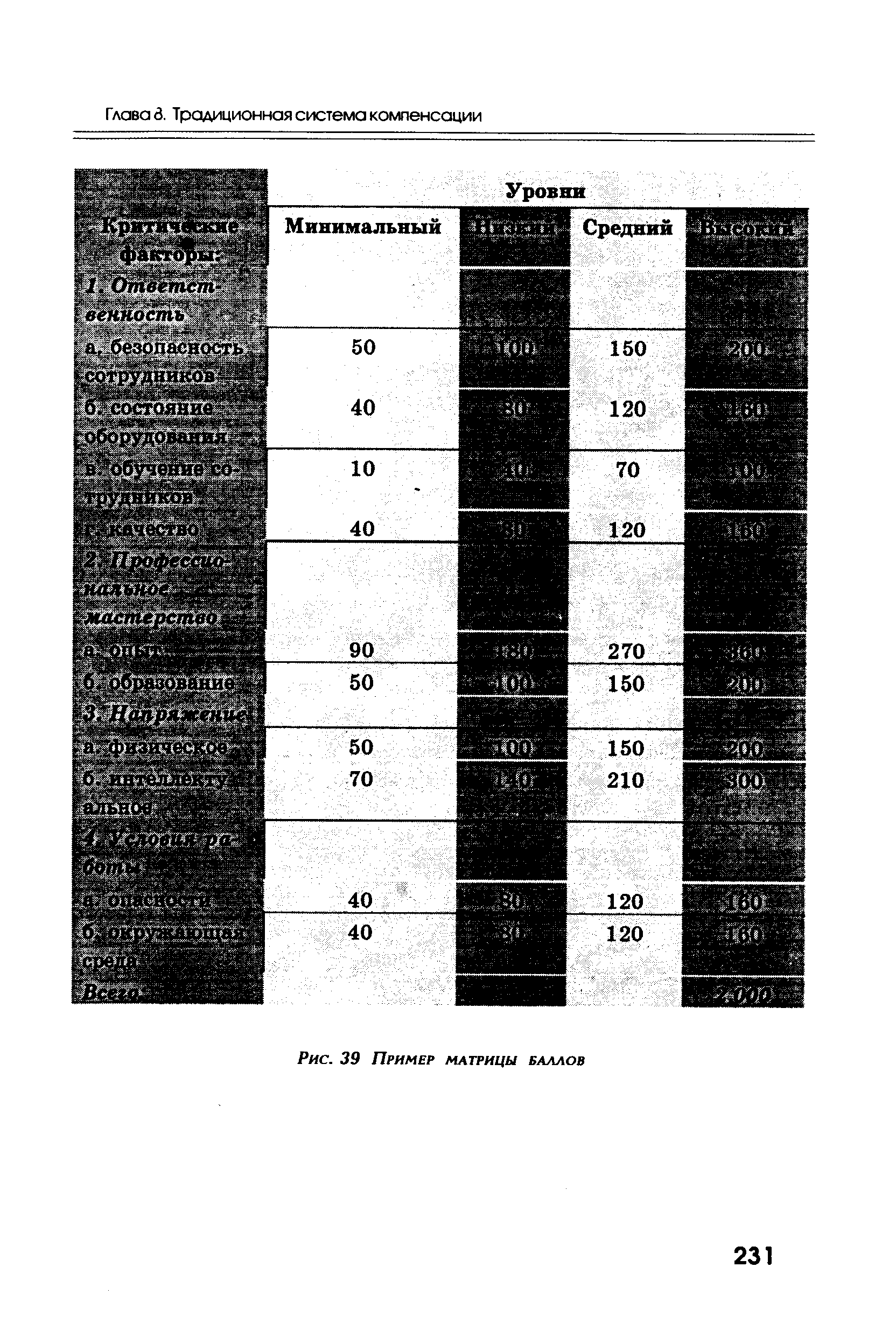 |
Рассмотрим пример матрицы ортогонального планирования 2-го порядка для случая k = 3 [c.275]
Построим матрицу загрузок для различных значений числа наладчиков / и количества швейных машину. Элементы такой матрицы обозначим By. Пример матрицы представлен в виде табл. 8.6. Как было показано выше, в оценочном и не совсем верном расчете, поиск оптимальных значений / и у можно начать со значений / = 3 и у = 3, пропустив меньшие значения (/ - число наладчиков, / = 3, 4, 5 у - число арендуемых швейных машин, у = 3,4, 5). [c.307]
Отметим, что в нашем примере матрица входящего сальдо AS(t - 1) является нулевой, т. е. она имеет следующий вид [c.17]
Примеры матриц (и векторов) этого вида приводятся ниже. [c.373]
| Таблица 4. Пример матрицы ключевых результатов | 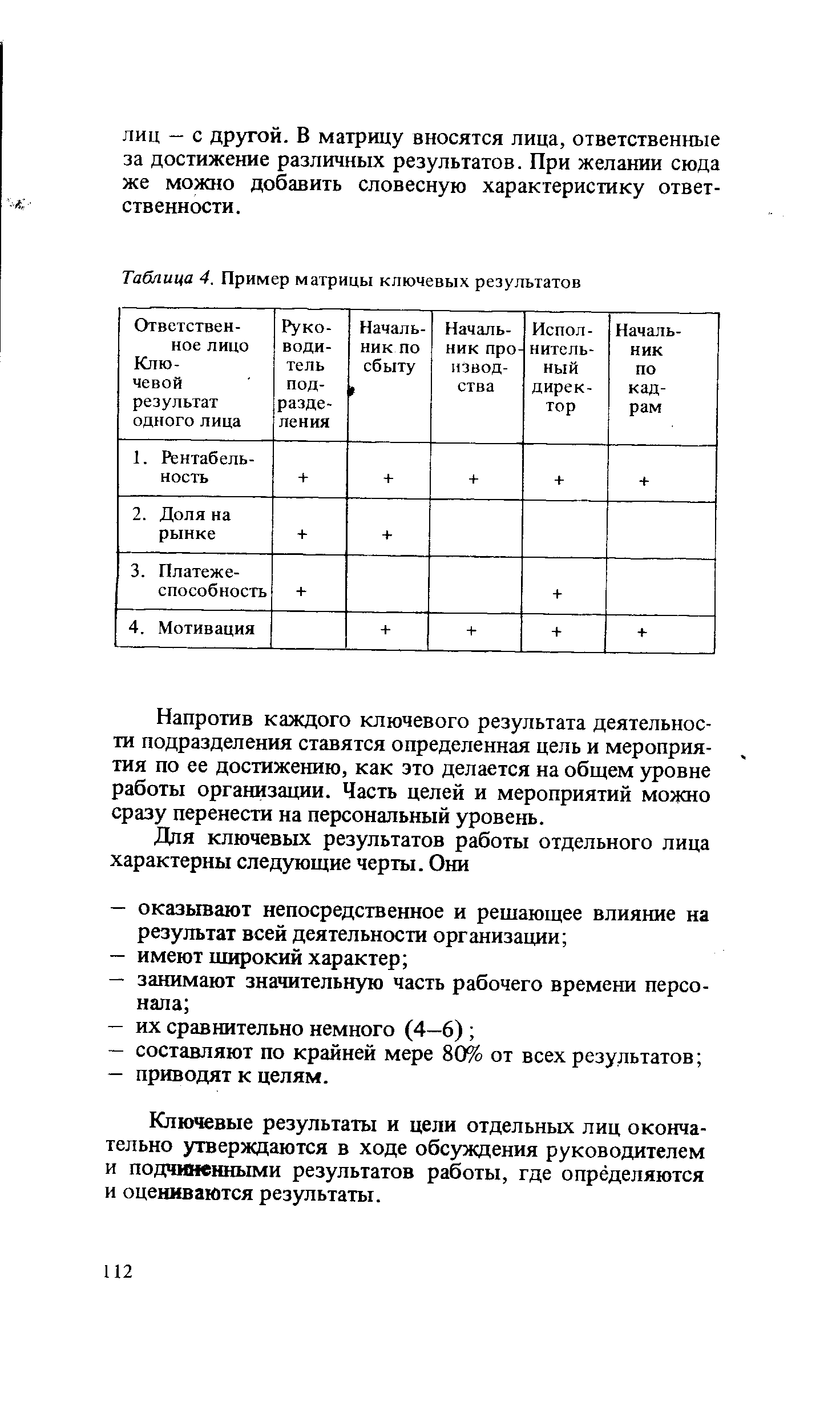 |
Рис, 4-10. Пример матрицы распределения ответственности по проекту конверсии программного [c.127]
Пример. Матрица А А неотрицательно определена для любой матрицы А. В самом деле, для любого вектора х [c.500]
В этом примере матрица А имеет размерность 4 х 4, а элементы матрицы вычисляются по определенной формуле. Показан вывод всей матрицы, а также некоторых ее элементов. [c.168]
Рассмотрим пример. Матрица парных коэффициентов корреляции признаков (выше главной диагонали) представлена в следующей таблице [c.42]
Каждый эксперт получает неполную матрицу, на осях абсцисс и ординат которой расположены сравниваемые параметры (рис. 2 - пример матрицы для случая пяти параметров). Заполняются только те клетки, которые находятся справа от нисходящей диагностики. [c.37]
Пример матрицы для определения групп продукта [c.62]
| Рисунок 17. Пример матрицы 2x2 | 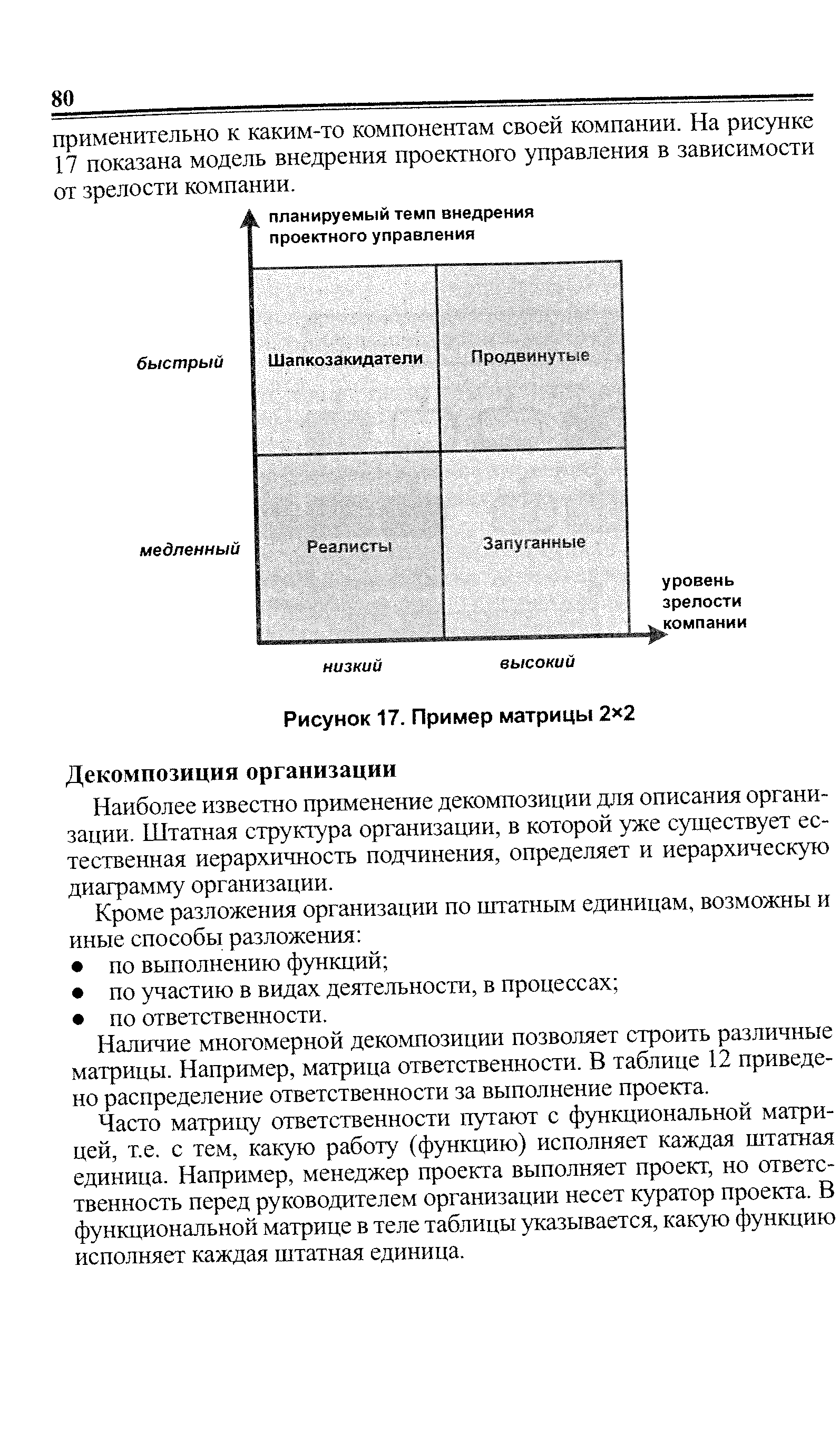 |
| Таблица 12. Пример матрицы ответственности |  |
Вероятность прямо влияет на определение ожидаемого значения — центральной концепции платежной матрицы. Ожидаемое значение альтернативы или варианта стратегии — это сумма возможных значений, умноженных на соответствующие вероятности. К примеру, если вы считаете, что вложение средств (как стратегия действий) в киоск для торговли мороженым с вероятностью 0,5 обеспечит вам годовую прибыль 5000 долл., с вероятностью 0,2 — 10 000 долл. и с вероятностью 0,3 — 3000 долл., то ожидаемое значение составит [c.237]
Продемонстрируем матричный способ построения модели на примере формирования матрицы для технологического комплекса с постоянными параметрами (табл. 24.1), включающего два производства (рис. 24.2). Практическая трудность здесь может состоять Е том, что эти производства не только выпускают готовые продукты, но и обмениваются между собой материальными потоками. Матричная развертка технологии в данном случае весьма наглядна п помогает не запутаться в нумерации многочисленных возвратных материальных потоков. [c.415]
Первое из указанных требований означает, что предназначенная к использованию в практике планирования модель (далее для краткости эти модели называются плановыми) должна быть ориентирована на решение конкретной планово-экономической задачи, предусмотренной существующей или проектируемой методологией планирования. Это диктует необходимость трансформации многих известных экономико-математических моделей. Так, например, классическая модель межотраслевого баланса позволяет рассчитывать сбалансированные объемы выпусков продукции при заданной матрице коэффициентов прямых затрат и известном конечном продукте. Однако на практике такая задача может возникнуть лишь на завершающем этапе работы над планом, когда уже -рассмотрены вопросы технической политики в отраслях и приняты соответствующие решения (а значит, известна матрица плановых коэффициентов прямых затрат), изучены и обоснованы объем и структура капитальных вложений, товарооборота, экспорта и импорта (а значит, известен конечный продукт). Между тем очевидно, что межотраслевые модели наибольшую пользу могут принести как раз на начальных стадиях работы над планом при проработке вариантов структурной политики. Поэтому на основе стандартного межотраслевого баланса необходимо разрабатывать различные постановки межотраслевых моделей, нацеленные на решение конкретных практических задач в данном режиме функционирования АСПР и на данной стадии разработки плана. Примерами таких постановок являются, в частности, оптимизационная межотраслевая модель корректировки заданий пятилетнего плана на очередной год для стадии формирования проекта [c.118]
Приведем пример. Значительная часть матрицы технологических коэффициентов планового межотраслевого баланса может формироваться (и в результате внедрения первой очереди АСПР в определенной мере уже формируется) по данным централизованных расчетов потребности в материальных ресурсах, выполняемых на ЭВМ. Это существенно снижает затраты труда плановых работников на выполнение наиболее трудоемкой процедуры построения межотраслевых моделей —процедуры формирования исходной информации. При этом входные данные для межотраслевого баланса являются лишь побочным , но очень важным продуктом автоматизации указанных прямых плановых расчетов. Однако если результаты расчетов по межотраслевой модели ограничить только вектором ее решения (для статической модели, например, это — вектор отраслевых объемов производства), то возможности анализа на основе этой модели будут чрезвычайно обеднены. Поэтому на практике межотраслевая модель дополняется задачей прямой обработки данных, на вход которой подается вектор решения модели, используемая в ней исходная информация, данные за предплановый период и некоторые другие данные (например, коэффициенты перехода от чистых отраслей к хозяйственным, от цен конечного потребления к оптовым ценам предприятий и др.), а на выходе формируется набор аналитических таблиц, всесторонне и в удобной для плановика форме характеризующий получаемый из решения модели вариант плана. [c.128]
Рассмотрим морфологический ящик на примере матрицы для часов, приведенной в работе немецких маркетологов Е. Дихтля и X. Хершгена (рис. 2.6). [c.90]
Для экспериментальной проверки указанных методов по достигаемым результатам и затратам времени на выполнение расчетов были взяты 15 примеров матриц операционных затрат времени на обработку партий деталей с однонаправленными технологическими маршрутами 1. В числе этих примеров одиннадцать матриц размером i X / = 6 X 12 и четыре матрицы 7 X 12. По технологическому процессу при обработке отдельных деталей занято от 7 до 11 станков. Характер матриц аналогичен приведенному в табл. 36 2. [c.185]
В табл. 4.6показан пример матрицы ответственности. Роли в примере указывают на вид участия подразделения в работе О — Ответственный исполнитель, И — Исполнитель, П — Приемка работ, К — Консультации. [c.297]
Теория жизненного цикла товара (ЖЦТ) получила широкое распространение в учебной литературе по маркетингу. В каждом учебнике ей посвящена как минимум отдельная глава, а число научных статей, описывающих жизнь товаров, не поддается учету. Она оказала влияние и на используемые маркетологами популярные методы планирования (к примеру, матрица БКГ или портфельный метод M Kinsey). [c.178]
Приведем два примера матриц Гессе для матричных функций. Во-первых, рассмотрим матричную функцию от п х 1 вектора х [c.251]
Применительно к рассматриваемому примеру матрица смежностей для прадерева (рис. 4.6) представлена на стр. 146—147. [c.145]
Второй пример матрицы создан под влиянием работ Л. Хольбе-ка-Ханссена. Матрица состоит из более детальных 6 х 6 ячеек. Она устанавливает следующие сектора собственную организационную структуру фирмы, ее потребителей, сбытовиков, конкурентов, поставщиков и, наконец, социальную среду. Эта матрица определяет также 6 уровней, а именно экономический, технический, социологический, психологический, биологический и геофизический. Как мы видим, обе матрицы имеют много общего. Основное различие состоит в том, что матрица 6x6 может дать возможность для более детального анализа участников рынка и их характеристик. [c.162]
Это неполный пример матрицы оценки риска, использованной а проекте Информационные Системы , занимающемся переходом от системы Windows Olfi e-97 к системе Windows-2000, Проектная команда выявила риски, такие, как зависание системы после установки, жалобы конечных пользователей на изменение и сопротивление им и плохую работу оборудования. Помимо оценки вероятности, серьезности и времени события, проектная команда также оценивала свою способность вовремя определить тот момент, когда соответствующее событие действительно будет иметь место, чтобы смягчить его последствия, Обратите внимание, что команда считает высокой степень трудности обнаружения события, связанного с зависанием системы, так как системы рушатся без предупреждения, а отказ пользователя получил среднюю оценку, так как растущее недовольство и сопротивление можно заметить задолго до того, как оно приобретет угрожающие размеры. [c.166]
Положительные матрицы очевидно строго коположительны. Однако, как показывают примеры, матрицы вида [c.24]
