В то время как современная теория портфеля определяет оптимальный вес составляющих портфеля (для достижения наименьшей дисперсии при заданном доходе или наоборот), она не затрагивает идею оптимального количества. Речь идет о том, что для данной рыночной системы есть оптимальное количество, которое можно использовать в торговле при данном уровне баланса счета, чтобы максимизировать геометрический рост. Это количество мы и будем называть оптимальным Данная книга предлагает, чтобы современная теория портфеля использовалась трейдерами на любых рынках, а не только на фондовом. Однако мы должны породнить современную теорию портфеля (которая дает нам оптимальный вес) с идеей оптимального количества (оптимальное f), чтобы добиться действительно оптимального портфеля. Именно этот оптимальный портфель может и должен использоваться трейдерами на любых рынках, включая фондовые. При торговле без заемных средств (т.е. без рычага ), например при управлении портфелем акций, вес и количество являются синонимами, но в ситуации с рычагом (например портфель фьючерсных торговых систем) вес и количество от- [c.11]
Как только мы изменим современную теорию портфеля и отделим вес от количества, то сможем вернуться к торговле акциями с этим теперь уже переработанным инструментом. Мы увидим, как почти любой портфель акций без рычага можно улучшить, превратив его в портфель с рычагом, соединив с безрисковым активом. В дальнейшем все станет вам интуитивно очевидно. Степень риска (или консервативности) является в таком случае функцией рычага, который трейдер желает применить к своему портфелю. Это означает, что положение данного трейдера в спектре неприятия риска зависит не от используемого инструмента, а от рычага, который он выбирает для торговли. Если говорить коротко, то книга научит вас управлению риском. Мало трейдеров имеют представление о том, что такое управление риском. Это не полное упразднение риска, поскольку тогда вы полностью упразднили бы выигрыш, и не просто вопрос максимизации потенциального дохода по отношению к потенциальному риску. Управление риском относится к стратегии принятия решений, которая имеет целью максимизацию отношения потенциальной прибыли к потенциальному риску при определенном приемлемом уровне риска. Чтобы понять это, мы должны сначала познакомиться с оптимальным f, компонентом уравнения, выражающим оптимальное количество для сделки. Затем мы должны научиться комбинировать оптимальное f с оптимальным взвешиванием портфеля. Такой портфель будет максимизировать потенциальную прибыль по отношению к потенциальному риску. Сначала мы раскроем эти концепции с эмпирической точки зрения (вкратце повторим книгу Формулы управления портфелем ), затем изучим их с более мощной точки зрения, параметрической. В отличие от эмпирического подхода, который использует прошлые данные, параметрический подход использует прошлые данные и некоторые параметры. Затем эти параметры используются в модели, дающей преимущественно те же ответы, что и эмпирический подход. Сильной стороной параметрического подхода является то, что вы можете изменить значения параметров, чтобы посмотреть, как изменится результат. Эмпирический подход не позволяет этого сделать. Однако эмпирические методы также имеют сильные стороны. Они в основном проще с точки зрения математики, поэтому их легче использовать на практике. По этой причине сначала рассматриваются эмпирические методы. В конце нашего исследования мы увидим, как применять данные концепции при заданном пользователем уровне риска, и узнаем стратегии, которые максимизируют рост. В книге рассмотрено очень много тем. Я попытался сделать ее настолько сжатой, насколько это вообще возможно. Некоторый материал может быть не совсем вам понятен, и, возможно, он поднимет больше вопросов, чем даст ответов. Если так оно и есть, значит я добился одной из целей этой книги. Большинство книг имеет одно сердце , одну центральную концепцию, из которой проистекает вся книга. Эта книга отличается тем, что у нее несколько таких концепций. Некоторые посчитают ее трудной, если подсознательно ищут книгу с одним сердцем . Я не приношу за это извинений это не ослабляет логики книги, наоборот, обогащает ее. Чтобы полностью понять материал, изложенный в книге, может быть, вам придется прочитать ее два или даже три раза. Одной из особенностей книги является более широкая трактовка концепции принятия решений в среде, характеризуемой геометрическими следствиями. Среда геометрического следствия — это среда, где количество, с которым вы должны работать сегодня, является функцией предыдущих результатов. Я думаю, что это освещает большую часть среды, в которой мы живем Оптимальное f— это регулятор роста в такой среде, а побочные продукты оптимального f говорят о скорости роста в данной среде. Из этой книги вы [c.12]
Современная теория портфеля [c.40]
| Рисунок 1-7 Современная теория портфеля | 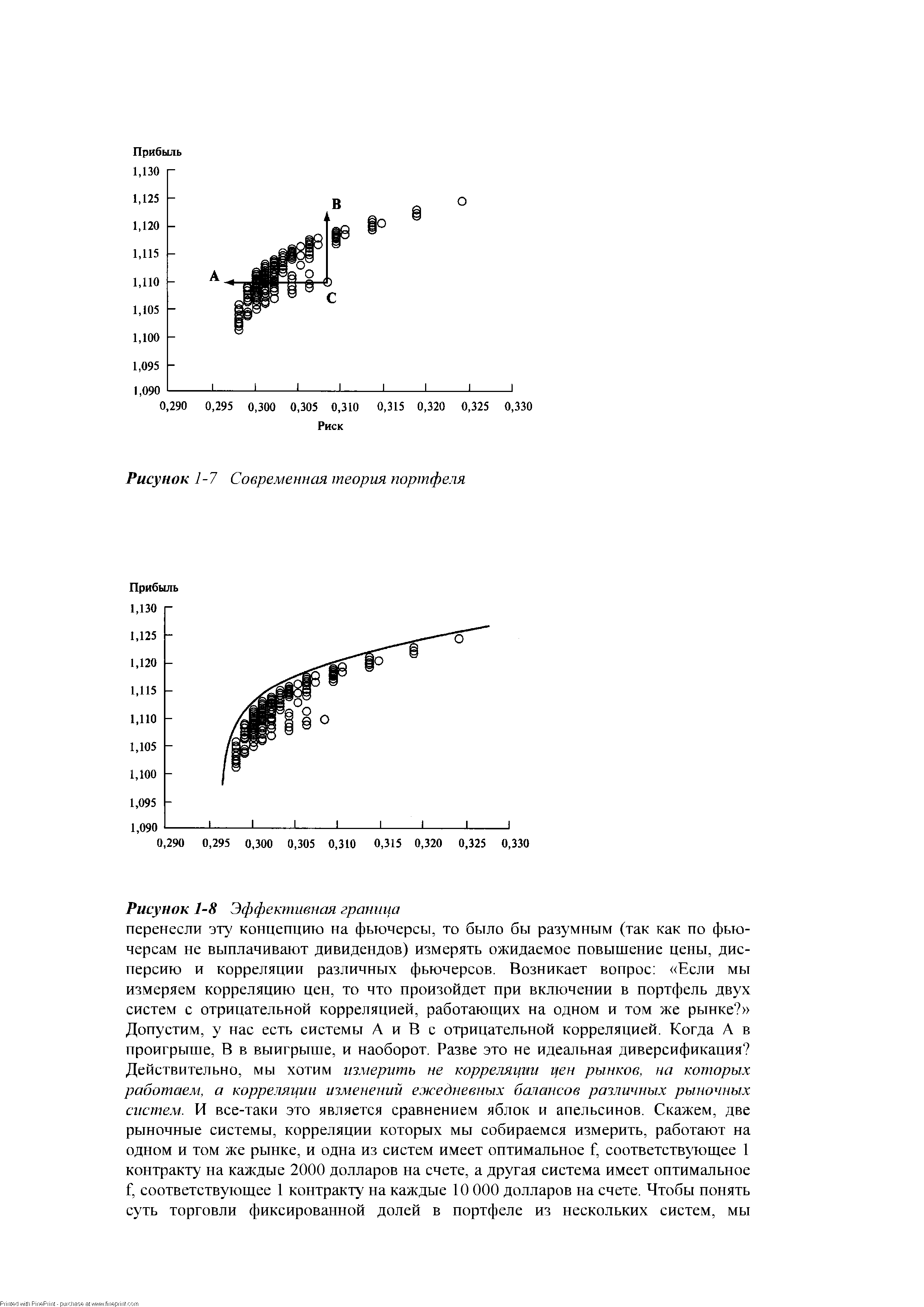 |
СОВРЕМЕННАЯ ТЕОРИЯ ПОРТФЕЛЯ [c.75]
Новый подход к диверсификации портфеля был предложен Гарри Марковичем, основателем Современной теории портфеля (1952 г.). Маркович утверждает, что подход инвестора к формированию портфеля ценных бумаг зависит исключительно от ожидаемого дохода и риска. Не вдаваясь в дебри математической статистики, приведем лишь суть теории Марковича. [c.77]
Так называемая современная теория портфеля (хотя она и была сформулирована в 1952 г.) дает дополнительный инструмент минимизации риска ковариацию (или корреляцию) между ценными бумагами. [c.131]
Правильное сочетание отклонений от рыночной пропорции зависит от степени различия в предпочтениях данного и среднего инвесторов и от дополнительного риска, связанного с такой стратегией. Сложный финансовый рынок требует использования всех средств современной теории портфеля для управления капиталом инвестора, который существенно отличается от среднего инвестора . Управление инвестициями в такой модели должно быть относительно пассивным после первоначального выбора портфеля его изменения невелики и происходят достаточно редко. [c.282]
О том, что использование современной теории портфеля не зависит от результатов тестирования САРМ, см. в статье [c.288]
Согласно современной теории портфеля финансовый аналитик стремится оценить потенциальную подверженность ценной бумаги влиянию основных факторов, а также возможный риск по этой бумаге, поскольку эти данные необходимы для определения риска всего портфеля (измеряемого показателем стандартного отклонения). Аналитик может попытаться также оценить ставку дивидендной доходности бумаги в следующем году, чтобы определить возможность ее включения в портфель, для которого ставка дивидендной доходности является важной характеристикой. Тщательный анализ таких вопросов, как дивидендная политика компании и вероятный приток средств инвесторов в будущем, могут стать источником более качественного прогноза по сравнению с простым экстраполированием прошлогодней ставки дивидендной доходности. [c.791]
Следует отметить, что, хотя данные стили были описаны с точки зрения современной теории портфеля, их можно реализовать и с использованием другой техники. Например, согласно современной теории портфеля оптимальный портфель акций (см. рис. 24.5(6)) определяется на основе прогнозов показателей ожидаемой доходности, стандартного отклонения и ковариации в сочетании с кривыми безразличия. После его нахождения управляющий портфелем определяет размеры инвестиций в отдельные виды обыкновенных акций. В то же время поиск такого портфеля можно осуществить посредством других действий. Нередко это происходит с использованием в большей степени качественных и в меньшей степени формальных параметров. [c.859]
Одним из основных вопросов современной теории портфеля является качество диверсификации на эффективном финансовом рынке любая разумная инвестиционная стратегия предполагает вложение средств в различные финансовые активы. В предыдущих главах были рассмотрены традиционные ценные бумаги, такие, как акции и облигации, и некоторые менее традиционные, такие, как опционы и фьючерсы. Однако инвестор также должен рассматривать инвестиции в иностранные ценные бумаги и материальные активы. [c.926]
Современная теория портфеля базируется на использовании статистических и [c.54]
Задача, решаемая на основании модели, дает ответ на вопрос о долях вложений в различные виды ценных бумаг в портфеле. При помощи "метода критических линий" устраняются портфели, не удовлетворяющие ограничениям, при этом остаются только эффективные портфели. Отобранные таким образом портфели объединяются в список, содержащий сведения о процентном составе портфеля из отдельных ценных бумаг, а также о доходе и риске портфелей. Выбор конкретного портфеля зависит от максимального риска, на который готов пойти инвестор. Эта модель занимает очень важное место в современной теории портфелей ценных бумаг. [c.377]
Отцом современной теории портфеля является Гарри Марковиц, получив ший за свои труды в 1990 г Нобелевскую премию по экономике 8 Первый урок, который дает нам теория Марковица, состоит в том, что, как правило, совокуп вый уровень риска может быть снижен за счет объединения рисковых активов в Портфели. Основная причина такого снижения риска заключается в отсутствии прямой функциональной связи между значениями доходности по большинству различных видов активов. Теория портфеля приводит нас к недвусмысленным выводам. 1) для минимизации риска инвесторам следует объединять рисковые активы в портфели 2) уровень риска по каждому отдельному виду активов еле дует измерять не изолированно от остальных активов, а с точки зрения его влияния на общий уровень риска диверсифицированного портфеля инвестиций [c.9]
СОВРЕМЕННАЯ ТЕОРИЯ ПОРТФЕЛЯ ВИДЫ ИНВЕСТИЦИОННЫХ РИСКОВ [c.75]
К книге рассмотрены новейшие подходы к выработке и принятию финансовых решений. Комплексно представлены финансовые рычаги управления, финансовые стратегии и методы оценки финансовых перспектив. В книге изложены методы определения денежных потоков для инвестиционного проекта корпорации, а также современная теория портфеля в принятии инвестиционных решений. [c.2]
Вторая часть книги посвящена методологии обоснования долгосрочных инвестиционных и финансовых решений. В ней показано, как определяются денежные потоки для инвестиционного проекта корпорации, каким образом формируется интегральный эффект проекта, а также отражена ключевая роль современной теории портфеля в принятии инвестиционных решений. [c.14]
Риск. В современной теории портфеля (МРТ) риск измеряется как стандартное отклонение доходностей ценных бумаг. [c.289]
Современная теория портфеля (МРТ). Обобщающее название для методов [c.289]
Современная теория портфеля 37 [c.37]
Современная теория портфеля 41 [c.41]
Для выработки инвестиционной политики главным является определение инвестиционной цели инвестора. Согласно современной теории портфеля цели инвестора проявляются в его отношении к риску и ожидаемой доходности. Одним из широко применяемых методов определения таких целей является построение кривой безразличия, характеризующей предпочтения инвестора. Это кривая на критериальной плоскости, состоящая из оценок эквивалентных портфелей. Выбор между портфелями, оценки которых лежат на такой кривой, безразличен для инвестора. Вместе с тем сравнение портфелей, оценки которых лежат на разных кривых, свидетельствуют, что любой портфель с оценкой на одной кривой предпочтительнее портфеля с оценкой на другой кривой. [c.347]
В отличие от бухгалтерского учета, история которого насчитывает не одно тысячелетие, финансовый менеджмент как самостоятельная наука сформировался относительно недавно. Отдельные разработки по теории финансов велись еще до второй мировой войны.В частности, широкую известность получили исследования Дж. Уильямса, разработавшего модель оценки стоимости финансового актива. Тем не менее принято считать, что начало этому процессу было положено в первой половине пятидесятых годов работами Г. Марковица, заложившими основы современной теории портфеля.В этих работах, по сути, была изложена методология принятия решений в области инвестирования в финансовые активы и предложен соответствующий научный инструментарий. [c.3]
Данный факт имеет очень большое значение в современной теории портфелей ценных бумаг. Отобранные таким образом портфели объединяют в список, содержащий сведения о процентном составе портфеля из отдельных ценных бумаг, а также о доходе и риске портфелей. Выбор конкретного портфеля зависит от максимального риска, на который готов пойти инвестор. [c.343]
Основные концепции современной теории портфеля изложены в монографии, написанной доктором Гарри Марковицем. Первоначально Маркович предположил, что управление портфелем является проблемой структурного, а не индивидуального выбора акций, что обычно практикуется. Марковиц доказывал, что диверсификация эффективна только тогда, когда корреляция между включенными в портфель рынками имеет отрицательное значение. Если у нас есть портфель, составленный из одного вида акций, то наилучшая диверсификация достигается в том случае, если мы выберем другой вид акций, которые имеют минимально возможную корреляцию с ценой первой акции. В результате этого, портфель в целом (если он состоит из этих двух видов акций с отрицательной корреляцией) будет иметь меньшую дисперсию, чем любой вид акций, взятый отдельно. Марковиц предположил, что инвесторы действуют рациональным способои и при наличии выбора предпочитают портфель с меньшим риском при равном уровне прибыльности или выбирают портфель с большей прибылью, при одинаковом риске. Далее Марковиц утверждает, что для данного уровня риска есть оптимальный портфель с наивысшей доходностью, и таким же образом для данного уровня доходности есть оптимальный портфель с наименьшим риском. Портфель, доходность которого может быть увеличена без сопутствующего увеличения риска или портфель, риск которого можно уменьшить без сопутствующего уменьшения доходности, согласно Марковичу, неэффективны. Рисунок 1-7 показывает все имеющиеся портфели, рассматриваемые в данном примере. Если у вас портфель С, то лучше заменить его на портфель А, где прибыль такая же, но с меньшим риском, или на портфель В, где вы получите большую прибыль при том же риске. Описывая эту ситуацию, Марковиц ввел понятие эффективная граница (effi ient frontier). Это набор портфелей, которые находятся в верхней левой части графика, то есть портфели, прибыль которых больше не может быть увеличена без увеличения риска, и риск которых не может быть уменьшен без уменьшения прибыли. Портфели, находящиеся на эффективной границе, называются эффективными портфелями (см. Рисунок 1-8). Портфели, которые находятся вверху справа и внизу слева, в целом недостаточно диверсифицированы по сравнению с другими портфелями. Те же портфели, которые находятся в середине эффективной границы, обычно очень хорошо диверсифицированы. Выбор портфеля инвестором зависит от степени неприятия риска инвестором — иначе говоря, от желания взять на себя риск. В модели Марковица любой портфель, который находится на эффективной границе, является хорошим выбором, но какой именно портфель выберет инвестор — это вопрос личного предпочтения (позднее мы увидим, что есть точное оптимальное расположение портфеля на эффективной границе для всех инвесторов). Модель Марковица первоначально была представлена для портфеля акций, который инвестор будет держать достаточно долго. Поэтому основными входными данными были ожидаемые доходы по акциям (определяется как ожидаемый прирост цены акции плюс дивиденды), ожидаемые дисперсии этих доходов и корреляции доходов между различными акциями. Если бы мы [c.41]
Именно так и происходило. Построение портфеля после Второй мировой войны обрело математическую строгость, которой ему не хватало ранее. До этого, как бывало во многих других областях, проходил этап накопления фактов, когда одинаково уместной кажется любая частичка информации. Впрочем, в рамках концепции, предложенной так называемой Современной Теорией Портфеля (иначе ее называют E-V-meopueu, или средне-дисперсионной моделью), были развиты уже более тонкие методы исследования. [c.26]
Исследования эффективности рынков, современные теории портфеля и финансов утверждают, что все инвесторы или средний инвестор не могут получать устойчивый выигрыш от операций на фондовом рынке, осуществляемых на основе анализа ценных бумаг. Механизм рыночного ценообразования, усердно раскручиваемый талантливыми аналитиками, слишком эффективен, чтобы позволить даже некоторым инвесторам постоянно извлекать более чем среднюю прибыль за счет отбора ценных бумаг. Но Грэм и Додд исходят из того, что механизм рыночного ценообразования и поныне в значительной степени основывается на ошибочных и зачастую иррациональных решениях, так что цены фондового рынка только время от времени случайно совпадают с внутренней стоимостью ценных бумаг, а большую часть времени колеблются вокруг этой величины. [c.9]
Современная теория портфеля была сформулирована Гарри Марковитцем в работе, опубликованной в 1952 году. Вкратце эта теория утверждает, что максимальный доход от портфеля не должен быть основой для принятия решения из-за элементов риска. Для сведения риска к минимуму портфель нужно диверсифицировать. Уменьшение риска, однако, означает и снижение доходности. Таким образом, при снижении риска доходы от портфеля должны быть оптимизированы. Фактически нужен такой портфель, в котором соотношение риска и дохода было бы приемлемым для инвестора. [c.131]
Целью современной теории портфеля является разработка методов, с помощью которых инвестор может выбрать оптимальный для себя портфель из бесконечного числа возможных. Для решения вопроса о включении каждой рассматриваемой ценной бумаги в портфель инвестору нужно оценить ее ожидаемую доходность и стандартное отклонение вместе со всеми ковариациями между этими ценными бумагами. Используя такие оценки, инвестор может определить кривую эффективного множества Мар-ковица. После этого для данной безрисковой ставки инвестор может найти касательный портфель и определить положение линейного эффективного множества. Наконец, инвестор может произвести инвестицию в этот касательный портфель и сделать заем или выдать кредит по безрисковой ставке. При этом сумма займа или кредита зависит от предпочтений инвестора относительно соотношения риска и доходности. [c.289]
Инвесторы, которые пользуются услугами более одного менеджера, могут остановить свой выбор на одном из них с тем, чтобы он помог на этой важной стадии, либо они могут воспользоваться услугами консультанта или специалиста по финансовому планированию. В любом случае главной характеристикой, отличающей одного клиента от другого, являются их инвестиционные цели. Согласно современной теории портфеля данные цели проявляются в отношении клиента к риску и ожидаемой доходности. Как упоминалось в гл. 7, одним из методов определения таких целей является построение кривой безразличия. В то же время определение кривой безразличия клиента является нелегкой задачей. На практике ее часто получают в косвенной и приближенной форме путем оценки уровня толерантности риска (risk toleran e), определяемой как наибольший риск, который клиент готов принять для данного увеличения ожидаемой доходности. [c.846]
Новый подход к диверсификации портфеля был предложен Гарри Марковнцем, основателем Современной теории портфеля (1952 г.). Марковнц утверждает, что подход инвестора к формированию портфеля ценных бумаг зависит исключительно от ожидаемого дохода и риска. Не [c.77]
Приравнивание инвестиций к биржевой игре продолжилось моделью опционного ценообразования Блэка-Шоулса и другими теориями на основе равновесия. Теории биржевой игры, включая современную теорию портфеля (Modern Portfolio Theory - MPT), не проводили различия между краткосрочными биржевыми спекулянтами и долгосрочными инвесторами. А почему [c.30]
Для большинства индивидуумов, которые обучены стандартной гауссовой статистике, идея бесконечных среднего или дисперсии кажется абсурдной или даже извращенной. Мы всегда можем вычислить дисперсию или среднее выборки. Как оно может быть бесконечным Еще раз повторим, что мы применяем частный случай, гауссову статистику, ко всем случаям. В семействе устойчивых распределений нормальное распределение - частный случай, который существует, когда а = 2,0. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует "дисперсии совокупности", к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп (Sharpe, 1963) говорил, что беты (в смысле современной теории портфеля (МРТ)) должны рассчитываться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а < 2,0, выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. Выборочные дисперсии, как ожидалось бы, будут неустойчивыми и не будут стремиться ни к какому значению, даже при увеличении объема выборки. Если а < 1,0, то же самое верно и для среднего, которое также не существует в пределе. [c.194]
Итак, Марковитц разработал очень важное для современной теории портфеля ценных бумаг положение, которое гласит совокупный риск портфеля можно разложить на две составные части. С одной стороны, это так называемый систематический риск, который нельзя исключить и которому подвержены все ценные бумаги практически в равной степени. С другой — специфический риск для каждой конкретной ценной бумаги, который можно избежать при помощи упраления портфелем ценных бумаг. При этом сумма сложенных средств по всем объектам должна быть равна общему объему инвестиционных вложений (например, часть сердств на банковском счете вводится в модель как инвестиция с нулевым риском), т.е. сумма относительных долей Xj в общем объеме должна равняться единице [c.342]
Смотреть страницы где упоминается термин Современная теория портфеля
: [c.44] [c.182] [c.210] [c.249] [c.313] [c.209]Смотреть главы в:
Интернет как инструмент для финансовых инвестиций -> Современная теория портфеля
Интернет как инструмент для финансовых инвестиций -> Современная теория портфеля
