Для более наглядного сравнения средних между собой на рис. 1.3. 2 приведены простая, взвешенная и экспоненциальная средняя для графика курса йены с периодом, равным 2 1. Ш Вычисление экспоненциальных скользящих средних [c.11]
Одним из наиболее широко используемых индикаторов являются средние линии. Различают простые, взвешенные и экспоненциальные средние. Это индикаторы, следующие за трендом, т.е. при наличии тренда работают хорошо. Однако примерно 70% времени цена движется в боковом канале. В таком режиме работы средние дают много ложных сигналов. [c.13]
Для более наглядного сравнения средних между собой на рис. 1.3.2 приведены простая, взвешенная и экспоненциальная средняя для графика курса иены с периодом, равным 21. [c.16]
Мы рассмотрели три типа среднего скользящего значения простой, линейно-взвешенный и экспоненциально-сглаженный. Кроме того, мы изучили различные комбинации таких показателей - применение одного среднего скользящего, а также комбинации двух или трех. При этом возник ряд вопросов. Разберем некоторые их них. [c.224]
Простое среднее скользящее оказалось эффективнее, чем линейно-взвешенное и экспоненциально-сглаженное. Оно наилучшим образом отражало динамику цен на десяти рынках (из тринадцати, на которых проводилось исследование), на двух - эффективнее оказалось линейно-взвешенное, а экспоненциально-сглаженное - только на одном, на рынке какао (см. табл. 9.4). [c.225]
По мере совершенствования компьютерных технологий было проведено большое количество исследований по развитию технических систем торговли на рынках товарных фьючерсов. По своей природе такие системы чисто автоматические (или механические), что подразумевает полное исключение из процесса человеческих эмоций и суждений. За последнее время такие системы были значительно усовершенствованы. Сначала при анализе использовались простые средние скользящие. Затем стали применяться методы двойного и тройного пересечения. Впоследствии появились линейно-взвешенные и экспоненциально-сглаженные средние скользящие. А совсем недавно в торговые системы стали включать также и довольно сложные статистические методы - например, метод линейной регрессии. Все эти системы прежде всего являются системами следования за тенденциями, то есть сначала они определяют основную ценовую тенденцию, а затем следуют за ней. [c.238]
Существуют различные количественные методы прогнозирования. Интуитивные подходы основываются исключительно на прошлом опыте. Подходы, основанные на сглаживании, - это метод скользящего среднего и экспоненциальное сглаживание. Оба метода используют в качестве базы для прогнозирования взвешенное усредненное значение данных прошлых периодов. [c.255]
Существует пять распространенных типов скользящих средних простое (его также называют арифметическим), экспоненциальное, треугольное, переменное и взвешенное. Скользящие средние можно рассчитывать для любого последовательного набора данных, включая цены открытия и закрытия, максимальную и минимальную цены, объем торгов или значения других индикаторов. Нередко используются и скользящие средние самих скользящих средних. [c.197]
Приведенный нами пример показывает, как высчитывается простое десятидневное среднее скользящее цены закрытия. Однако существуют и другие, гораздо более сложные виды средних скользящих. Существует множество вопросов относительно того, как наилучшим образом использовать средние скользящие. Например существует ли оптимальная временная протяженность периода расчета усредненных показателей Какие средние значения следует использовать кратковременные или долговременные Существуют ли оптимальные средние скользящие для всех рынков или для каждого рынка в отдельности Является ли цена закрытия наиболее оптимальной ценой, которую следует учитывать Не лучше ли использовать несколько средних скользящих Какой тип средних скользящих лучше простой, линейно взвешенный или экспоненциально сглаженный Существуют ли периоды, в которые эти показатели более значимы, чем в остальное время [c.208]
| Рис. 9.26 Сравнительный пример двадцатидневных средних скользящих линейно-взвешенного (сплошная линия) и экспоненциально-сглаженного (пунктир). Экспоненциально-сглаженная кривая является также взвешенной, однако учитывает всю предшествующую динамику цен. Больший вес также придается показателям цен за последние дни. | 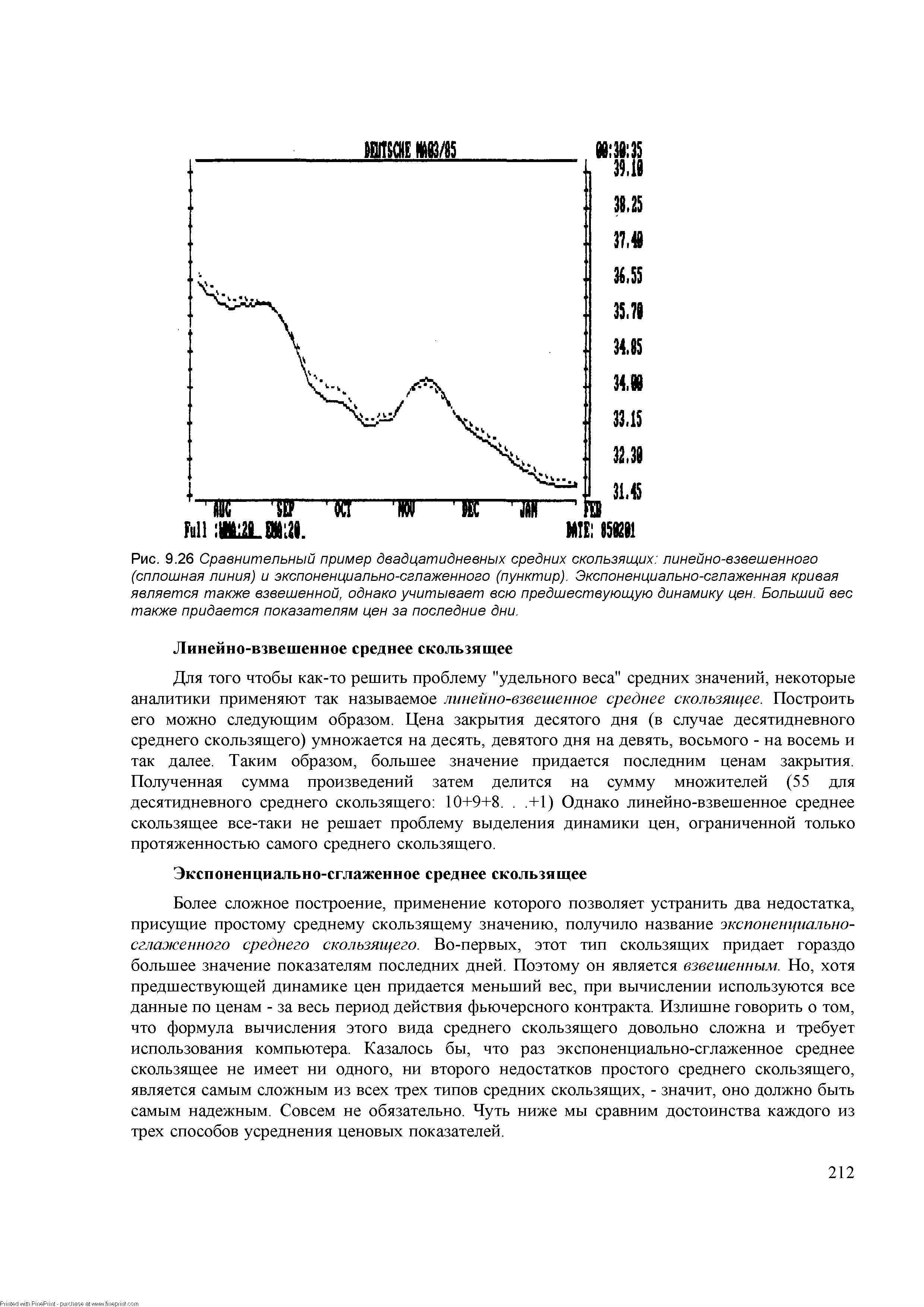 |
Формулы (25.5) настолько хорошо подобраны, что графики простой и экспоненциальной скользящих средних не слишком сильно отличаются друг от друга для не слишком больших одинаковых периодов п, и вопрос Что лучше, а что хуже относится к вопросам вкуса и привычки. Заметим лишь, что для больших периодов (п> 100), как правило, используются простые средние без взвешивания. Для средних и малых значений п трейдеры и аналитики чаще предпочитают пользоваться взвешенными средними. [c.254]
Схема прогнозирования для рассматриваемого примера представлена в табл. 7,3 при значении а = 0,2. Здесь UQ = 6 — прогноз, полученный экспертным методом. Результаты прогноза спроса на седьмой месяц методом скользящего среднего (т6 = 5) и экспоненциально взвешенного среднего (м7 = 5,34) отличаются на величину 0,34. [c.125]
Подобно пробоям, скользящие средние привлекательны в своей простоте и чрезвычайно популярны среди технических трейдеров. Входы могут генерироваться с использованием скользящих средних различным образом в рынок можно входить, когда цена пересекает скользящую среднюю вверх когда быстрая средняя пересекает медленную когда наклон скользящей средней меняет направление или когда цены взаимодействуют со скользящей средней, как с уровнями поддержки/сопротивления. Кроме того, разнообразия добавляет существование простых, экспоненциальных, взвешенных и многих других скользящих средних. Поскольку модели входа часто используют те или иные варианты пробоев или скользящих средних, эти методы важно рассмотреть в подробностях. [c.93]
Экспоненциальное сглаживание - популярный метод краткосрочного прогнозирования. Использует взвешенное среднее данных прошлых периодов как основу для прогнозирования. При этом большие весовые коэффициенты присваиваются более поздним данным и меньшие - данным наблюдений прошлых периодов. Считается, что будущее больше зависит от более близкого прошлого и меньше - от удаленных по времени наблюдений. [c.249]
При таком усреднении большее отражение получают относительно недавние цены закрытия. Последнее достигается умножением цены первого дня выбранного интервала на 1, второго дня - на 2 и т.д., т.е. сомножителем для цены каждого последующего дня является номер дня в выбранном ряду дней, после чего сумму этих произведений делят на сумму номеров дней. Наиболее изощренным из известных вариантов скользящего среднего является ЭСС - экспоненциально сглаженное (взвешенное) скользящее среднее (см. рисунок 5.37.). В дополнение к применению весовых коэффициентов при усреднении цен, при вычислении ЭСС учитываются все предыдущие цены за время наблюдения за динамикой цен, а не только цены в выбранном рабочем интервале. [c.89]
Единственное, чем скользящие средние разных типов существенно отличаются друг от друга, — это разные весовые коэффициенты, которые присваиваются последним данным. В случае простого скользящего среднего все цены рассматриваемого периода имеют равный вес. Экспоненциальные и взвешенные скользящие средние делают более весомыми последние цены. Треугольные скользящие средние придают больший вес ценам в середине периода. И, наконец, переменные скользящие средние изменяют весовые коэффициенты в зависимости от волатильности цен. [c.197]
Это основная статистика. В общем, картина не самая блестящая, но вполне солидная. Однако эти показатели не базируются на оптимальных параметрах. Что произойдет, если мы пожелаем произвести оптимизацию параметров, чтобы получить максимальную прибыль Тогда мы должны оптимизировать все три параметра одновременно, чтобы установить их наилучшую комбинацию. Поэтому я протестировал разные значения для скользящих средних с периодом от 4 до 19с приращением в 1. Для долгосрочной скользящей средней были испытаны числа от 20 до 50 с приращением 1. Каждый из этих тестов затем был проверен для различных видов скользящих средних простой, смещенной, экспоненциальной и взвешенной. [c.189]
Лучший результат при пересечении со смещенной скользящей средней похож на второй результат, но с чистой прибылью, которая меньше, и составляет 57.000 долларов. Однако для этого потребовалось 34/57 сделок со средней торговлей в 1.000 при проседании капитала, равном 5.600 долларов. При этом использовалось 6-дневная краткосрочная средняя и 25-дневная долгосрочная средняя. При использовании взвешенной скользящей средней мы получаем прибыль, которая тоже чуть меньше - 57.000 долларов, и при этом заключается 18/36 сделок. Коэффициент выигрыш/проигрыш равен 4,0, и при этом средняя торговля составляет 1.600 долларов. Падение капитала также допускается в разумных пределах на уровне в 5.600 долларов. Экспоненциальная скользящая средняя дала сравнительно слабый результат она обеспечила всего 23.000 профита при 32% выгодных торгов при максимальном падении капитала, равном 10.000 долларов. Средняя торговля оставалась все еще на уровне в 700 долларов. [c.190]
Возможности этого пути иллюстрирует приведенное ниже сравнение предсказаний двух типов комитетов из 25 экспертов (см. Рисунок 14 и Рисунок 15). Предсказания проводились по одной и той же схеме в качестве входов использовались экспоненциальные скользящие средние приращений ряда с периодами равными первым 10 числам Фибоначчи. По результатам 100 экспериментов взвешенное предсказание дает в среднем превышение правильно угаданных знаков над ошибочным равное примерно 15 тогда как среднее - около 12. Заметим, что общее число повышений курса над понижением за указанный период как раз равно 12. Следовательно, учет общей тенденции к повышению в виде тривиального постоянного предсказания знака "+" дает такой же результат для процента угаданных знаков, что и взвешенное мнение 25 экспертов. [c.162]
Более сложное построение, применение которого позволяет устранить два недостатка, присущие простому среднему скользящему значению, получило название экспоненциально-сглаженного среднего скользящего. Во-первых, этот тип скользящих придает гораздо большее значение показателям последних дней. Поэтому он является взвешенным. Но, хотя предшествующей динамике цен придается меньший вес, при вычислении используются все данные по ценам - за весь период действия фьючерсного контракта. Излишне говорить о том, что формула вычисления этого вида среднего скользящего довольно сложна и требует использования компьютера. Казалось бы, что раз экспоненциально-сглаженное среднее скользящее не имеет ни одного, ни второго недостатков простого среднего скользящего, является самым сложным из всех трех типов средних скользящих, - значит, оно должно быть самым надежным. Совсем не обязательно. Чуть ниже мы сравним достоинства каждого из трех способов усреднения ценовых показателей. [c.212]
Различают 3 основных типа скользящих средних -простую, экспоненциальную и взвешенную. [c.169]
Потенциальный недостаток этого метода заключается в том, что в нем самые старые и последние показатели имеют равную значимость, а показатели, вышедшие за рамки расчета среднего, не учитываются вовсе. При расчете экспоненциально взвешенного скользящего среднего, или при экспоненциальном сглаживании, вклад показателя в прогноз уменьшается по мере его старения, так что наиболее свежие данные оказывают наибольшее влияние. Формула расчета экспоненциально взвешенного скользящего среднего следующая [c.143]
Рассмотрим результаты исследований, полученные этой группой, и их практическое применение в анализе рынка с помощью средних скользящих. Хокхаймер опубликовал некоторые первоначальные результаты исследований в статье под названием "Компьютеры помогут вам в игре на фьючерсных рынках". Эта статья была опубликована в 1978 году в ежегоднике "Коммоди-тиз". С 1970 по 1976 год были протестированы средние скользящие по каждому месяцу исполнения по тринадцати наименованиям товарных активов. Временной промежуток, покрываемый средними скользящими, которые были использованы в исследовании, составлял от трех до семидесяти дней. Данные тестов по простым, линейно-взвешенным и экспоненциально-сглаженным средним скользящим были сведены в таблицы по отдельности с целью определения оптимального значения для каждого рынка (см. табл. 9.1-9.3). Полученные результаты были, в свою очередь, сведены в сравнительную таблицу (см. табл. 9.4) с целью определения наиболее эффективного из трех типов средних скользящих. [c.224]
Скользящее среднее (Moving average). Индикатор тренда, который наилучшим образом работает в случае наличия тренда. Скользящее среднее сглаживает колебания цен, однако работает с задержкой по времени. Можно использовать любое число скользящих средних с различными временными интервалами усреднения, чтобы получать сигналы к покупке и продаже. Если используется только одно среднее, то сигнал к покупке поступает, если цена закрытия пересекает скользящую среднюю. Если используются два средних, сигнал к покупке подается в случае, когда короткая средняя пересекает снизу вверх более длинную . Технические аналитики используют три разновидности скользящей средней простую, взвешенную и экспоненциальную. [c.312]
Тригг показал, что интервал изменения у значения контрольного сигнала от — 1 до "+ . Он также доказал, что этот сигнал имеет определенные границы, соответствующие выбранному уровню доверия (табл. 4. 1). Для метода ИЛ) используется одна и та же константа сглаживания (а), что для вычисления экспоненциально взвешенной ошибки (et), среднего абсолютного отклонения (MAD,) и для вычисления прогноза. Как правияо, здесь значения а берут равными либо 0,1, либо 0,2. [c.51]
Существуют много видов скользящих средних. Мы рассмотрим три основных вида показателя среднего движения курса простой, или линейный (Simple MA), взвешенный (Weighted MA) и экспоненциальный (Exponential MA). [c.6]
При т= и модифицированный индикатор превращается в обычный. Этот индикатор впервые был реализован в торгово-аналити-ческом терминале SmartTrade. Там же предусмотрена возможность выбора вида скользящих средних простая и экспоненциально взвешенная. [c.296]
Используя рекуррентное соотношение для всех ровней ряда, начиная с первого и кончая моментом уровня (, можно получить, что экспоненциальная средняя, т е сглаженное данным меточом. значение уровня ряда, является взвешенной средней всех предшествующих уровней [c.415]
Exponential Moving Average (Экспоненциальное скользящее среднее). Индикатор более чувствителен, чем простое скользящее среднее такой же длины, и менее чувствителен, чем взвешенное скользящее среднее такой же длины. [c.181]
На следующем рисунке представлены 25дневные скользящие средние различных типов простое, экспоненциальное, взвешенное, треугольное и переменное. [c.203]
Как и в случае взвешенной средней, экспоненциальная скользящая средняя придает больший вес последним данным, однако при расчете используется вся история цен. Рекуррентная формула для ее вычисления имеет вид EMAt = t-yt+(l-a)- EMAt v [c.157]
После просмотра буквально тысяч наборов данных с широким разнообразием комбинаций бестрендовости (простые, взвешенные, экспоненциальные и с иными математическими вычислениями скользящих средних, построенных от медиан, максимумов, минимумов, закрытий и т.д.), я пришел к окончательному заключению, что лучшими вариантами являются [c.111]
Вычисляя среднее, мы складываем все цены с одинаковыми весами, тем самым значимость прошлых цен точно такая же, как и текущих. Более интересным может оказаться применение взвешенных средних, когда берется не простое арифметическое среднее, а взвешенное среднее — складываются цены закрытия с разными весовыми коэффициентами. Причем значимость прошлых цен за счет подбора таких коэффициентов значительно понижается по сравнению с последними данными. Этот подход позволяет ускорить появление сигналов. В дальнейшем мы столкнемся с экспоненциально сглаженным средним при обсуждении такого осциллятора, как MA D (см. 7.2.8). При построении ЕМА— экспоненциально сглаженного среднего — каждое следующее его значение получается как сумма текущей цены закрытия с большим коэффициентом и с маленьким коэффициентом берется историческое воспоминание о прошлом . [c.148]
