Простая двумерная структура [c.218]
Мы уже говорили, что процесс превращения иерархической или сетевой структуры данных в реляционную называется нормализацией. Внешне эта операция очень проста, но содержит некоторые нюансы, игнорирование которых может привести к неприятностям. Нюансы эти заключаются в том, что даже для простых двумерных структур приходится подправлять состав полей. Существует строгая теория нормализации, однако смысл ее можно понять на простых примерах. [c.233]
Двумерные структуры. Переход от одномерных к двумерным структурам сопровождается усложнениями качественного характера, и на построение точных решений задачи на ячейке рассчитывать больше не приходится. Тем не менее в ряде исключительных случаев удается, не отыскивая полно- [c.386]
Рассмотрим двумерную структуру, описываемую одной искомой функцией и. Согласно (9.33) [c.387]
В основе построения осредненного лагранжиана двумерных структур лежит следующее замечательное свойство двойственной вариационной задачи оказывается, что ее удается привести к тому же виду, что и исходную вариационную задачу. Установим этот факт. [c.387]
Растущая клеточная структура для задачи коммивояжера представляет из себя вначале кольцо из трех ячеек нейронов. Каждый нейрон характеризуется двумерным вектором w(, определяющим его положение на плоскости. Каждому нейрону в кольце приписывается также своя величина погрешности st, которая вначале полагается равной нулю. Дальнейшая [c.118]
Управление сложными портфелями, таким образом, требует применения двумерной матрицы подразумеваемой волатильности. Одно измерение — по ценам исполнения, а другое — во времени. Используемые отдельные волатильности должны отражать как можно точнее опционные цены на действующем рынке. С течением времени структура матрицы подразумеваемой волатильности может измениться, и это будет еще одним источником неопределенности, который должен быть рассмотрен. [c.202]
Теперь обсудим, каким образом МДЦ можно использовать при наличии дополнительной информации об относительной важности критериев в случае, когда множество возможных решений состоит из бесконечного числа элементов (например, задано в виде множества решений некоторой системы линейных неравенств). Для иллюстрации сначала рассмотрим самую простую ситуацию, — когда имеется всего три критерия и первый критерий важнее второго с некоторым коэффициентом относительной важности. Будем считать, что другой информации нет, причем получающееся в результате учета этой информации множество парето-оптимальных векторов бесконечно. Спрашивается, каким образом произвести дальнейшее сужение области поиска или же более того — остановить выбор на каком-то одном из возможных векторов С этой целью можно по известной формуле 612/1 + (1 - 0i2)/> пересчитать менее важный второй критерий и, тем самым, образовать новый векторный критерий, в котором первый и третий остались прежними. Именно второй, измененный критерий следует взять в качестве некоординатного и задать определенный ряд его значений для получения соответствующих двумерных сечений. Сравнивая представленные на дисплее сечения, можно получить наглядное представление о структуре множества Парето, соответствующем новому векторному критерию, и попытаться выбрать из этого множества какой-то один определенный (компромиссный) вектор у, у, у )- Этот [c.168]
Термин организационная структура сразу же вызывает в нашем воображении двумерную древовидную схему, состоящую из прямоугольников и соединяющих их линий. Эти прямоугольники показывают выполняемую работу и круг обязанностей и, таким образом, отображают разделение труда в организации. Относительное положение прямоугольников и соединяющие их линии показывают степень подчинения. Рассматриваемые соотношения ограничены двумя измерениями вверх-вниз и поперек, так как мы оперируем с ограничивающим допущением, согласно которому организационная структура [c.80]
Другим вариантом является организационная структура Тегеранского института управления в промышленности, который, кстати, разрабатывал описанную выше систему здравоохранения и социального обеспечения. Институт состоит из двух частей, каждая из которых представляет собой двумерную матрицу программ и операций предоставляемые услуги являются общими для обеих частей (рис. 8.5). Операции могут [c.160]
Представленная в данной главе многомерная организация имеет нечто общее с так называемыми матричными организациями [11]. Однако последние обычно являются двумерными и не обладают многими важными чертами рассмотренных организационных структур, особенно в вопросах финансирования. Кроме того, им всем присущ один общий недостаток сотрудники функционального подразделения находятся в двойном подчинении, что, как правило, приводит к нежелательным результатам. Именно этот наиболее часто отмечаемый недостаток матричных организаций является причиной так называемой профессиональной шизофрении . [c.163]
Двумерная трактовка стилей лидерства отражает дальнейшее развитие представления об эффективном руководстве. Исследователи из группы университета Огайо выявили серьезную ошибку в концепции разделения руководителей на тех, кто сосредоточен только на работе или только на человеке. Они разработали систему, согласно которой поведение руководителя классифицировалось по двум параметрам структуре и вниманию к подчиненным. Структура подразумевает такое поведение руководителя, когда он планирует и организует работу группы и свои взаимоотношения с ней с учетом конкретной структуризации производственных задач (предстоящей работы). Было выявлено, что руководители могут вести себя с различной степенью внимания к подчиненным и структуризации производственных задач (проблем). Возможные четыре комбинации ситуаций и поведения руководителя приведены на рис. 6.1. [c.151]
Типичную структуру системы зрительного восприятия [3, 12, 30, 44] можно представить следующим образом. Первичная информация об объемной сцене снимается телевизионным датчиком и фиксируется в виде матрицы двумерного распределения яркостей в плоскости проекции. Эта информация обрабатывается специальным набором аппаратных и программных процедур, выделяющих первичные характерные признаки в изображении линии, их пересечения, области однородности и т. д. [c.30]
Во-первых, программа Вальца по духу своему синтаксическая. Программа содержит таблицу возможных вершин и на некотором уровне может производить разбиение сцены на части. Но важно отчетливо представлять себе, что это программа с существенными семантическими корнями. Таблица не является просто совокупностью частных и чисто эмпирических данных. Она выведена в результате анализа разнообразных двумерных изображений реальных трехмерных структур. Полученное множество обозначений вместе с программой, которая их использует, правомерно считать лаконичной формой отражения ограничений, накладываемых реальной структурой на характер линий и вершин на изображении. [c.60]
Показанную на фиг. 1,е форму можно рассматривать не только как изображение буквы Т, но и как изображение трехмерного тела. Наша способность видеть в этом рисунке букву Т должна включать понимание того, что штрихи могут быть выражены или представлены не только простыми двумерными областями, как было показано раньше, но и простыми телами. В соответствии с развитой в разд. 2 теорией представлений эта способность связана с описанием структуры данных из двух областей, между которыми имеется более или менее сложное соответствие. Ниже будет продемонстрирована возможность решения этой задачи и будет описан алгоритм установления соответствия между контурными изображениями и трехмерными сценами. [c.98]
Кроме того, наше восприятие размерности может изменяться в зависимости от нашего расстояния от объекта. С некоторого расстояния орегонская пихта напоминает двумерный треугольник. Когда мы подходим ближе, она производит впечатление трехмерного конуса. Подойдя еще ближе, мы уже можем различить ее ветви, и она выглядит как сеть одномерных линий. Исследование с более близкого расстояния показывает, что ветви - это трехмерные трубки. Евклидова геометрия также испытывает трудности с размерностью созданий Демиурга и с возрастающей сложностью. Евклидовы структуры, напротив, становятся проще по мере уменьшения масштаба. Трехмерное твердое тело уменьшается до двумерной плоскости. Двумерная плоскость складывается из одномерных линий и, наконец, из безразмерных точек. Наше восприятие дерева, с другой стороны, шло от двумерного к трехмерному, затем к одномерному, а затем обратно к трехмерному. Такое восприятие отличается от евклидова восприятия. [c.14]
| Рис. 5.5.1. Организационные структуры в двумерном пространстве направление интеграции — уровень структуризации | 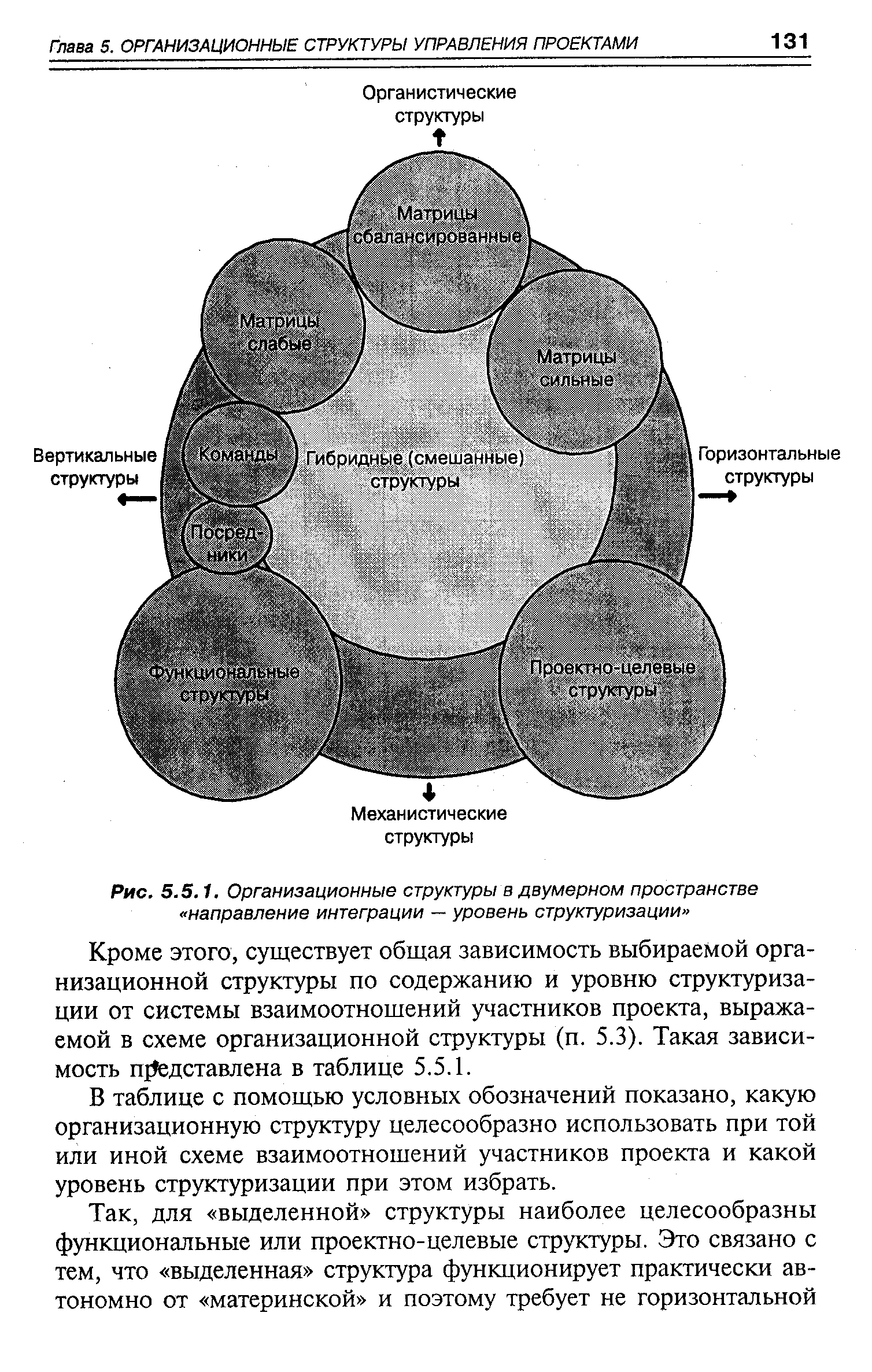 |
| Рис. 8.2.1. Двумерный анализ структуры и емкости рынка | 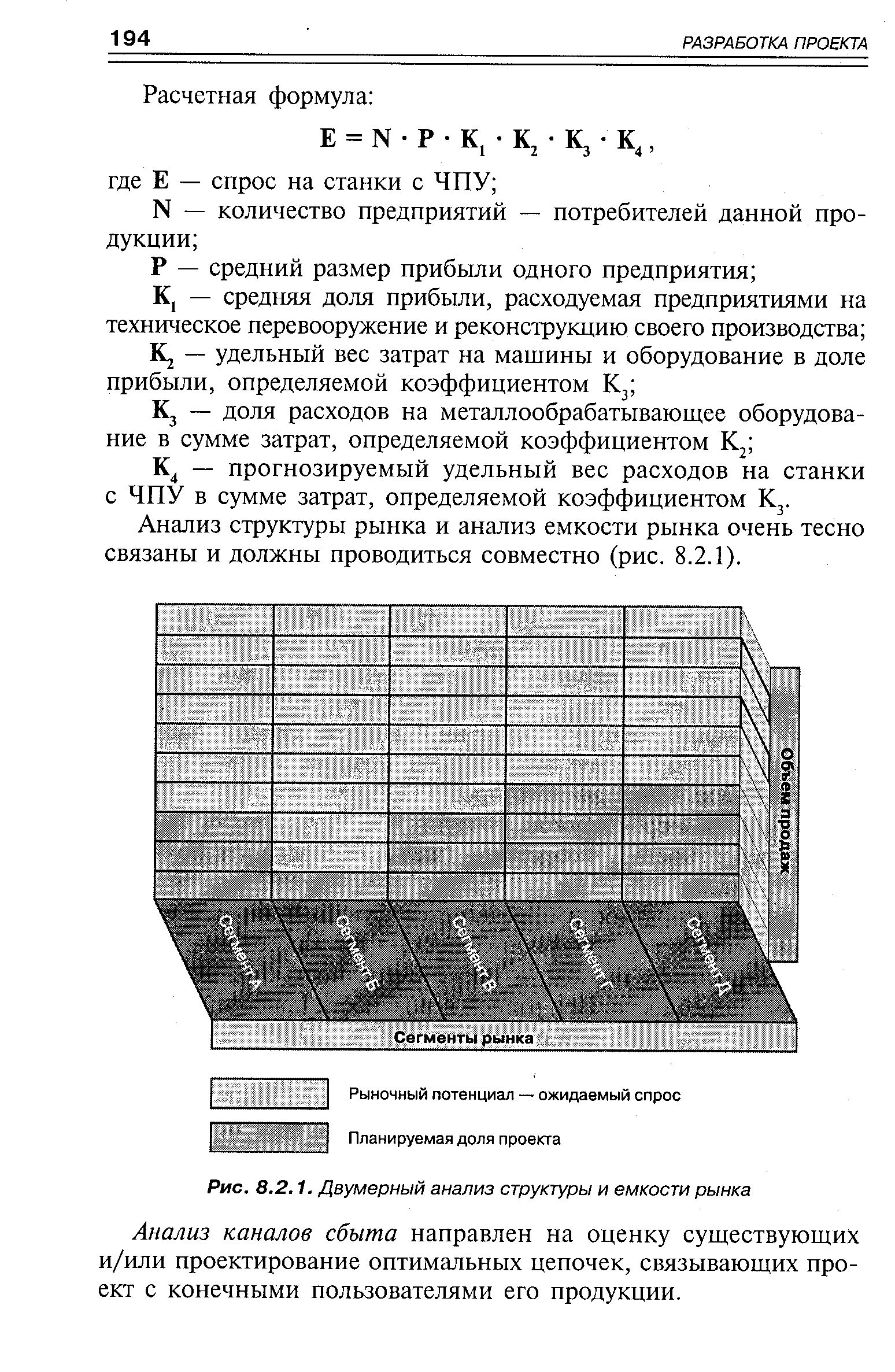 |
Итак, мы познакомились с двумя типами информационных структур — простой двумерной (телефонный справочник) и иерархической (справочник цен), причем иерархическую структуру мы механически свели к простой двумерной. [c.227]
Существуют и более сложные — сетевые — структуры, в которых каждый порожденный элемент может иметь более одного порождающего элемента. Эти структуры тоже можно свести к простым двумерным таблицам. [c.227]
Организационно-технологическая нормаль управления (ОТНУ) — организационный документ, отображающий отношения субъекта и структуры предметов управления с учетом разделения труда, механизма хозрасчетных отношений, используемой информационной технологии, количества управляемых объектов, а также иерархии хозяйственного и административно-авторитарного руководства двумерная таблица, реальное количество и состав строк которой соответствуют набору производственно-технологических, производственно-хозяйственных или административно-хозяйственных функций самостоятельного хозрасчетного подразделения с указанием объектов управления и частоты обращения к ним, а число столбцов — предельно возможному в реальных условиях (в зависимости, прежде всего, от формы собственности, концентрации производительных сил и территориального разделения труда) разделению процесса самоуправления на составляющие его операции. [c.609]
СОК является непараметрической регрессионной методикой, которая часто используется для формирования двумерного отображения входных данных с сохранением исходной топологии. СОК относится к разряду нейронных сетей, обучаемых без учителя, и представляет собой способ выявления взаимосвязей в структуре дан- [c.203]
Если общий объем признака подразделен по одному группиро-вочному признаку, а затем каждый групповой и общий объем снова подразделены по другому группировочному признаку, то образуется многомерная, в простейшем случае - двумерная - структура с пересекающимися признаками. [c.444]
Основное различие между СОК и ИСОГ заключается, очевидно, в типах карт, которые создают эти два алгоритма. С геометрической точки зрения отличительные особенности ИСОГ и СОК состоят в способе представления ими пространства входных данных. Основная идея, на которой основана архитектура ИСОГ, состоит в выявлении существенных особенностей входных данных, динамике их изменения и настройке на них, дающей карте возможность решать , в каком направлении эволюционировать. Следовательно, начав с исходной карты небольшой размерности, ИСОГ будет развиваться во вполне определенном направлении, выделяя те особенности входных данных, которые посчитает наиболее перспективными. Рост карты может контролироваться, поскольку индексация новых генераций отлична от индексации предшествующих. Таким образом, мы сохраняем двумерную структуру карты, даже если на практике нейроны окажутся организованными в различные слои в соответствии с моментом их создания. Окончательный результат применения метода ИСОГ оказывается совершенно отличным от того, которого можно было бы ожидать при обучении с помощью одного только метода СОК. [c.161]
Группа в Университете штата Огайо разработала двумерную модель поведения руководителя. Исследователи классифицировали руководителей по уровню внимания к подчиненным и к структуре, считая, что самое эффективное — это сочетать оба аспекта. На опкмк этой комцопции Блэйк и Мутон применили [c.511]
Методы второй группы направлены на.то, чтобы дать человеку представление об эффективном множестве в целом. Далее, человек может сам выбрать то эффективное решение, которое устраивает его в наибольшей степени. Надо сказать, что в том случае, когда число показателей превышает два, эта задача является весьма сложной. Она усугубляется тем, что даже для линейных задач множество эффективных точек является певыпуклым. Для систем с выпуклыми множествами допустимых решений п линейными показателями эту трудность можно преодолеть, если дать представление о всем множестве достижимых значений показателей. В указанном случае это множество является выпуклым, поэтому его структуру можно понять па основе анализа различных двумерных сечений этого множества. Заметим, что при этом одновременно дается представление о структуре эффективного множества, которое является частью границы множества достижимых показателей. [c.61]
Итак, двумерная пересекающаяся структура позволяет рассчитать пять видов структурных показателей (долей). При трех пересекающихся признаках группировки число разных видов структур достигает 19. В общем виде при п взаимопересекающихся признаках структура содержит (п3 — п2 + 1) видов долей. [c.445]
В результате такого обучения мы получаем не только квантование входов, но и упорядочивание входной информации в виде одно- или двумерной карты. Каждый многомерный вектор имеет свою координату на этой сетке причем чем ближе координаты двух векторов на карте тем ближе они и в исходном пространстве. Такая топографическая карта дает наглядное представление о структуре данных в многомерном входном пространстве, геометрию которого мы не в состоянии представить себе иным способом. Визуализация многомерной информации является главным применением карт Кохонена. [c.85]
Напомним, что методом. дающим оптимальное представление информации в виде координат двумерной сетки, является построение топографических карт (карт Кохонена), о которых шла речь в Главе 4. Напомним в двух словах суть этой методики. В многомерное пространство данных погружается двумерная сетка. Эта сетка изменяет свою форму таким образом, чтобы по возможности точнее аппроксимировать облако данных. Каждой точке данных ставится в соответствие ближайший к ней узел сетки. Таким образом каждая точка данных получает некоторую координату на сетке. Такое отображение локально непрерывно близким точкам на карте соответствуют близкие точки в исходном пространстве (обратное, вообще говоря, не верно близким точкам в исходном пространстве могут соответствовать далекие точки на карте -такова цена понижения размерности). Таким образом, распределение данных на двумерной карте позволяет судить о локальной структуре многомерных данных. [c.192]
Как уже отмечалось (гл. 3), обычный способ графического представления организационной структуры в виде двумерного дерева ограничивает число и характер возможных вариантов решения возникающих проблем. При наличии такого ограничения невозможны решения, обеспечивающие развитие организации с учетом технических и социальных изменений, темпы которых все больше и больше ускоряются. По мнению Олвина Тоффлера [32], наша неспособность учесть быстро меняющиеся условия и приспосабливаться к ним, неспособность, которую он назвал шоком будущего , является основной причиной многих кризисных ситуаций. Наличие таких ситуаций — очевидный факт, тем не менее до сих пор нет единого подхода к решению проблемы выхода из подобных ситуаций. Поэтому не-" удивительно, что системы управления предприятиями и общественными институтами США, а также их организационная структура во многих отношениях находятся на недостаточном уровне. [c.149]
В соответствии с общепринятой точкой зрения одним из основных результатов исследований по искусственному интеллекту явилось отыскание эффективных представлений проблемных ситуаций (1, 2]. Большинство аргументов в пользу того, что эта тематика имеет центральное значение, было высказано в связи с программами разрешения проблемных ситуаций, или решения задач (см., например, [3]). Указанный результат имеет принципиальное значение и в таких задачах, которые считаются чисто перцептивными, где для облегчения распознавания и других форм интерпретации были разработаны языки описания структуры двумерных образов. Одним из факторов, определяющих сложность или простоту языка описания, является возможность автоматического соотнесения ( присвоения ) структурных описаний с входными данными, т. е. задача грамматического разбора. Однако очевидно, что бессмысленно разрабатывать алгоритм грамматического разбора до того, как будет выбрана форма описания. Такое отграничение формы описания от процесса соотнесения описаний с входными данными напоминает проведение различия между знанием языка и его использованием, которое Хомский отметил в своих работах [c.89]
Одна из связанных с подходом Минского задач состоит в том, чтобы определить, какие дескриптивные предложения следовало бы присвоить данному конкретному образу. Фактически решение этой задачи равнозначно формулированию некоторой теории композиции образа, которая, по-видимому, должна лежать в основе интуитивного понятия класса изображений. Как показал Кирш [11], эта задача весьма близка к задаче описания предложений естественного языка, например английского. Отсюда Кирш сделал вывод, что для решения обеих задач можно использовать одни и те же средства, а именно порождающую грамматику. Некоторые попытки создания так называемых грамматик изображений были основаны на использовании грамматических правил, формат которых был двумерным 11, 13, 14]. Таким образом, синтаксис этих языков отражал синтаксис языка самих объектов, что соответствует традиционному требованию, предъявляемому к порождающей грамматике. В других работах, особенно в работах Ледли (15], Нарасимхана [16] и Шоу [17], для определения классов изображений были предложены более удобные линейные правила, имеющие структуру цепочек. Довольно подробный обзор этих разработок приведен в работе [12]. Общий недостаток этих работ состоит в том, что предложенные в них понятия композиции образов основаны на использовании очень узкого набора отношений. Так, например, разработанная Киршем грамматика прямоугольных треугольников содержит только пространственные отношения локальной близости элементов прямоугольного растра, т. е. смежность по вертикали, по горизонтали и по диагонали. Упомяну- [c.92]
Второе важное отличие состоит в том, что программа Робертса в явном виде вычисляет положение точки наблюдения. Этот важный аспект описания сцены в изложенном нами алгоритме совсем не затрагивается. Отсюда следует, что в установленном по этому алгоритму соответствии между трехмерной сценой и двумерным изображением координата z отсутствует. Описанная таблицей предикатов (табл. 4) связь характеризует внешнее выражение моделей углов в разных условиях видимости через соединения линий. Модели Робертса — это структуры данных, которые описывают все поверхности, ребра и углы многогранника безотносительно к условиям видимости. Условия видимости определяются лишь после нахождения точки наблюдения для каждой модели. В рамках описанного здесь алгоритма точка наблюдения характеризуется в терминах подклассов моделей, которые соответствуют вариациям условий видимости поверхности и ребра. Такое соответствие между изображением и сценой никак нельзя свести к числовому соответствию, в то время как в программе Робертса это комбинация вычислений (тригонометрические преобразования), топологического сопоставления и процедур удаления линий, соответствующих загороженным ребрам и точкам их пересечения. [c.126]
Описанная схема дает возможность делать выводы о структуре сцены в терминах любого из этих видов соответствия. Роберте переводит двумерный массив значений зачерненности в контурный рисунок, соответствие которого исходной сцене можно задать в виде простых условий. Однако следует подчеркнуть, что Роберте обрабатывал фотографии очень хорошо освещенных сцен, благодаря чему указанный перевод удавалось производить относительно надежно. Попытки повторить эту работу для менее тщательно освещенных сцен к успеху не привели. Необходимость в надежном контурном рисунке, по-видимому, вытекает из характера использованных Робертсом моделей и самого процесса интерпретации. Очевидно, что для точного определения точки наблюдения, а также содержания сцены необходимо идентифицировать все элементы изображения, соответствующие элементам модели (ребрам, углам, поверхностям), которые должны быть видимы при рассмотрении этой модели из предполагаемой точки наблюдения. Описанный здесь алгоритм определяет точку наблюдения в терминах условий видимости и предиката hind, т. е. очень грубо. По-видимому, это может позволить избежать необходимости в построении [c.127]
Мы уже исследовали одно такое фазовое пространство, аттрактор Лоренца (Глава 6). Здесь фазовая диаграмма никогда не повторяется, хотя она ограничена формой "глаза совы". Они "притягивается" к этой форме, которую часто называют ее "точкой притяжения (аттрактором)". Если мы исследуем линии в пределах аттрактора, мы находим самоподобную структуру линий, вызванную повторным сворачиванием аттрактора. Непересекающаяся структура линий означает, что процесс никогда не заполнит свое пространство полностью. Его размерность, таким образом, является дробной. Фрактальная размерность аттрактора Лоренца составляет приблизительно 2,08. Это означает, что его структура немного больше, чем двумерная плоскость, но меньше чем трехмерное тело. Следовательно, он также является созданием Демиурга. [c.229]
Подходы, описанные выше, послужили основой для разработки системы управления безопасностью Национального банка Республики Башкортостан (НБ РБ). Еще в 1994-1995 гг. в Национальном банке Республики Башкортостан велись работы по поиску наиболее оптимальной структуры обеспечения безопасности банка. Первым опытом систематизации структуры управления безопасностью явилась разработанная в 1995 г. концепция безопасности НБ РБ, в которой использован матричный подход к построению системы защиты. Данный подход предполагал создание перечня защищаемых ресурсов банка, выявление и классификацию вероятных угроз, разработку двумерной матрицы защитных мер, которые должны быть реализованы в точках пересечения вероятных угроз и защища- [c.194]
Можно доказать, что любую структуру данных можно преобразовать в простую двумерную таблицу. Мы уже говорили, что такое представление является наиболее удобным и для пользователя, и для машины, — подавляющее большинство современных информационных систем работает именно с такими таблицами. Базы данных, которые состоят из двумерных таблиц, называются реляционными. В этом термине нет ничего таинственного (по-английски relation — отношение), и вы вполне можете рассматривать его как краткий синоним неуклюжего словосочетания простые двумерные таблицы . [c.227]
Базовыми понятиями Я. а. являются описания, выражения и операторы. Описания задают атрибутивную информацию для определяющих вхождений лексем. Атрибуты лексем в основном характеризуют тип (вид) значений , вычисляемых в ходе выполнения программы, представление значений и способы их хранения в памяти вычислит, машины. В проблемно-ориентированных Я. а. предусматриваются описания величин, естественных для той области применения, на к-рую рассчитан данный язык. Так, кроме простых арифметич., логнч., литерных (текстовых) величин, можно описывать одномерные массивы простых величин — векторы, двумерные массивы — матрицы и т. д. В нек-рых Я. п. предусматриваются агрегаты величин — структуры, составляемые из простых величин различных типов. Описание структуры задаёт, кроме имени её самой, имена и тины её составных частей и отношения подчинения частей друг другу. Значением структуры может быть, напр., содержание нек-рого делового документа. Чтобы иметь возможность представлять в вычисле- [c.589]
В типичных группах сейсмоприемников 3-D, структура выносов является нелинейной, т.е. имеется мало ближних выносов и много дальних выносов (рис. 2. 19). Фактически, в широкоазимутных съемках распределения выносов являются линейными в области квадратов выносов (см. Раздел 3.3). В узкоазимутных съемках отмечается тенденция к распределениям выносов, которые являются в большей степени линейными распределение выносов двумерного профиля является конечным элементом. Пунктирная линия на рис. 2. 19 пред- [c.49]
Мы построили эту книгу таким образом, чтобы облегчить ее изучение при помощи примеров. Используя описания применении данного метода, предоставленные различными авторами, мы показываем, как можно обнаруживать структуры в больших наборах данных и каким образом данные большой размерности могут отображаться в виде двумерных изображении. От применения СОК в реальной жизни мы переидем к описанию самого метода, существуюших для этого программных средств и наиболее удачных примеров его реализации. [c.33]
В третьей главе мы перейдем от прогнозирования процентных ставок к управлению портфелем активов. В ней Гвидо Дебок показывает, каким образом с помощью самоорганизующихся карт многомерные данные по взаимным инвестиционным фондам могут быть представлены в виде простых двумерных карт, доступных восприятию руководителей этих фондов. Основываясь на данных, публикуемых корпорацией Morningstar , он исследует паттерны (образы) в структуре данных о взаимных инвестиционных фондах. Несколько показателей из базы Morningstar используются им в качестве входных данных. Далее автор показывает, каким образом СОК позволяет упростить классификацию фондов и создать таблицы для обеспечения принятия решений, более информативные по сравнению с простыми сортированными списками, построенными исходя из единичных и множественных критериев. Данный подход иллюстрирует визуальное представление информации по взаимным инвестиционным фондам, построение эталонных тестов и выведение более приемлемых показателей для сравнения эффективности помещения средств в различные взаимные фонды. [c.34]
Смотреть страницы где упоминается термин Двумерные структуры
: [c.100] [c.231] [c.168] [c.94] [c.127] [c.228] [c.18]Смотреть главы в:
Вариационные принципы механики сплошной среды -> Двумерные структуры
