КРИВАЯ ЭФФЕКТИВНОЙ ДОХОДНОСТИ [c.223]
На каждом сегменте финансового рынка существует зависимость между доходностью финансового инструмента и сроком до его погашения, причем такая зависимость стабильна только на одном сегменте и может иметь совершенно иные значения на другом. Эта зависимость получила название кривой эффективной доходности. В данном случае время до погашения является мерой риска вложения в актив чем дольше срок вложений, тем меньше уверенности, что должник вовремя и в полном объеме погасит долг, а соответственно больший риск инвестиций. [c.223]
На рисунке 6.7 приведена кривая эффективной доходности нормального вида. [c.223]
| Рис. 6.7. Кривая эффективной доходности |  |
В соответствии с теорией рациональных ожиданий кривая эффективной доходности отражает ожидания инвесторов относительно будущей доходности финансовых инструментов. Так, отрицательный наклон кривой эффективной доходности может означать ожидания инвесторов снижения доходностей на финансовом рынке. [c.223]
Из наблюдения за изменением кривой эффективной доходности можно сделать следующие выводы [c.224]
Кривая эффективной доходности выпукла вверх. Такой вид кривой эффективной доходности можно объяснить достаточно просто. Кредитор каждый раз требует дополнительной премии за предоставление средств в кредит на более длительный срок. Действительно, при увеличении сроков заимствования возрастает неопределенность, а соответственно и риск невыплаты долга. Следовательно, должна возрасти премия за риск. [c.224]
Однако далеко не всегда на финансовом рынке наблюдается нормальный вид кривой эффективной доходности, так как бывают аномалии, и, чем менее стабилен развитой рынок, тем причудливее и невероятнее бывает ее вид. Например, в декабре 1995 г. кривая эффективной доходности по ГКО имела вид, приведенный на рисунке 6.8. [c.224]
| Рис. 6.8. Кривая эффективной доходности на рынке в декабре 1995 г. | 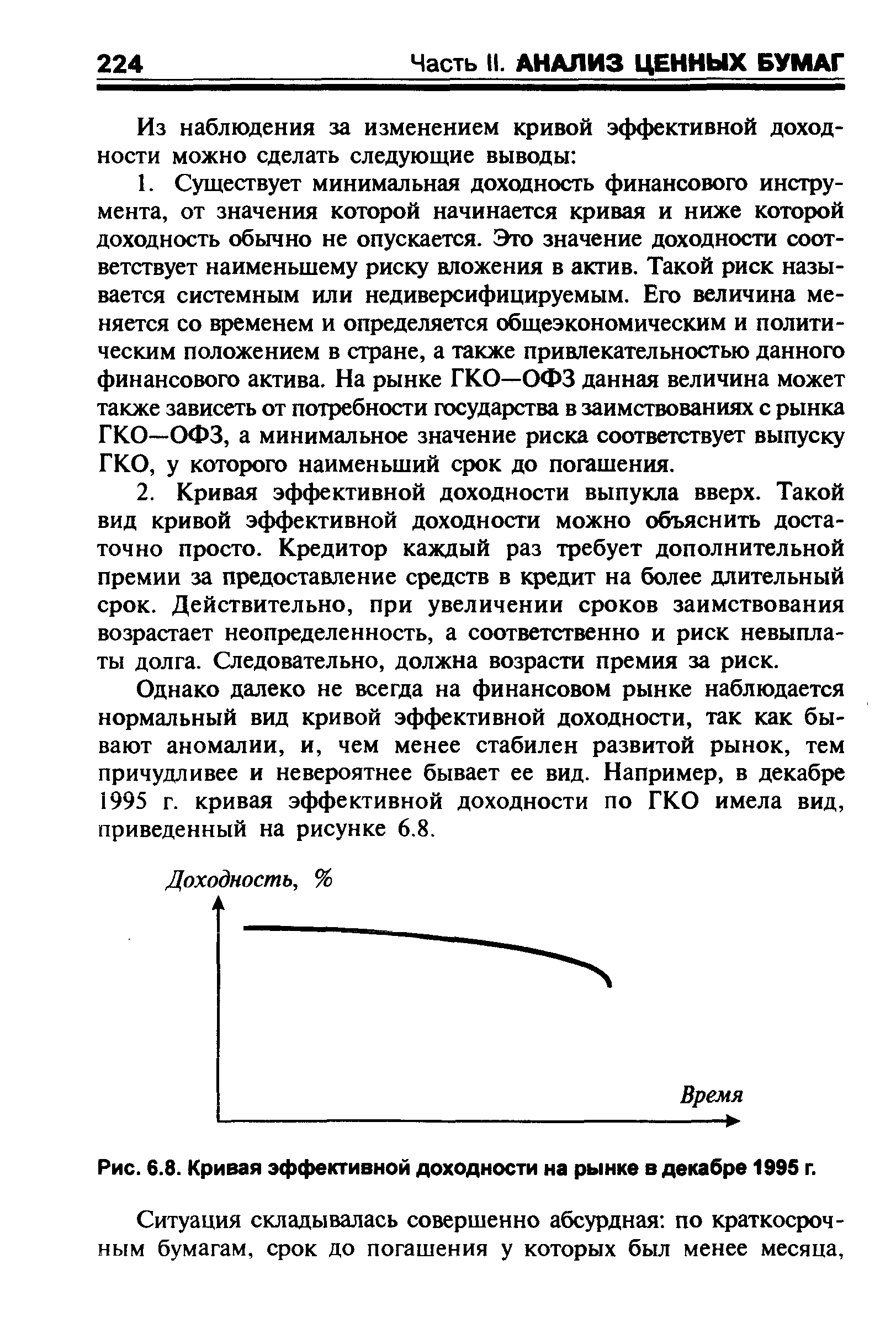 |
Кривая эффективной доходности, ее значения и форма, активно используются в основном для принятия решения о межвременном инвестировании и является задачей о временной структуре процентной ставки. Суть данной задачи состоит в определении оптимальной структуры инвестирования с учетом [c.225]
Пример. Предположим, кривая эффективной доходности имеет следующий вид (рис. 6.9) [c.226]
| Рис. 6.9. Кривая эффективной доходности (для примера) | 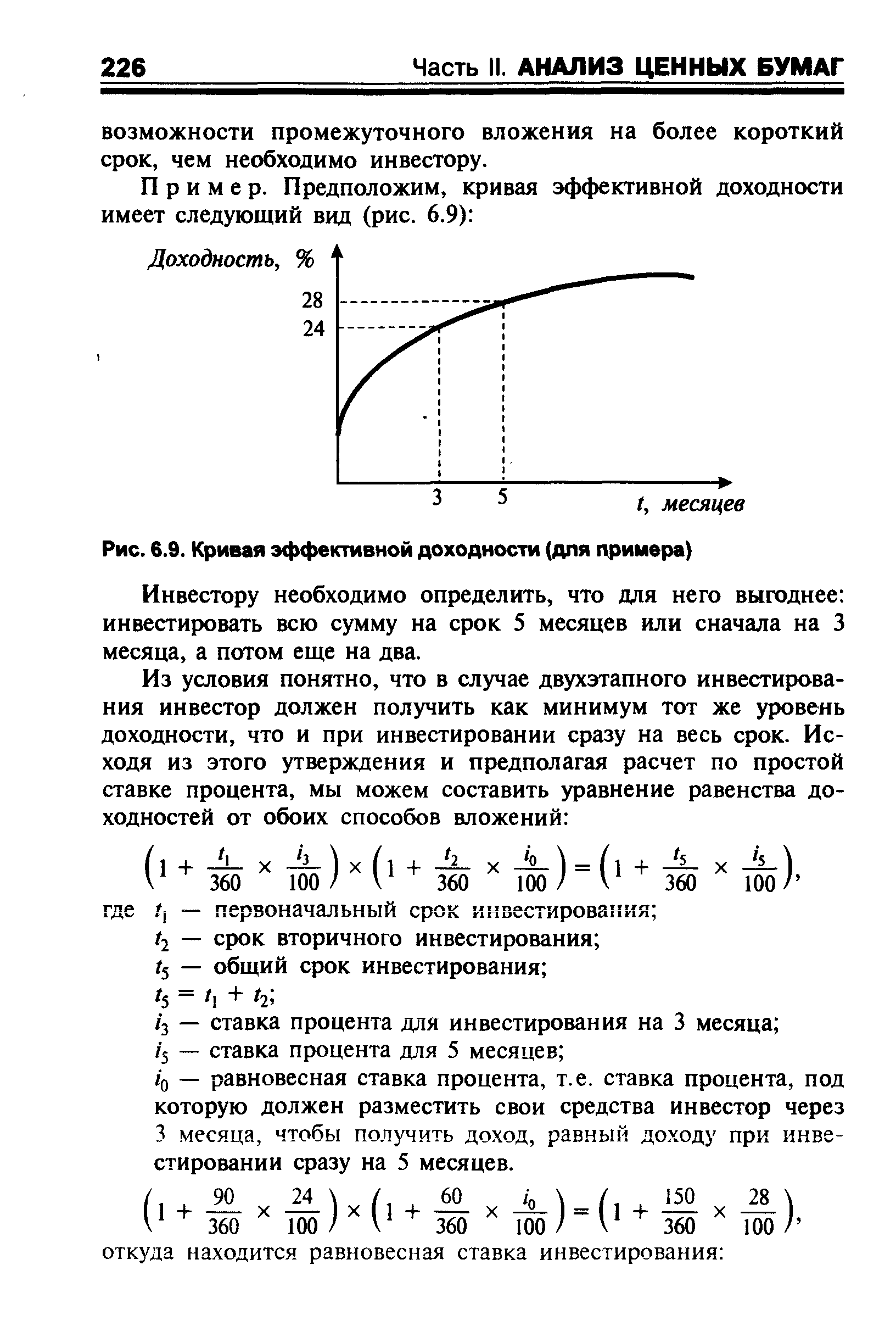 |
Предположение о том, что доходности ценных бумаг реагируют на общие для них факторы, значительно упрощает задачу вычисления кривой эффективного множества Марковица. [c.310]
На рис. 4.7 слева изображена кривая эффективности с (гипотетической) снижающейся ветвью. Рассмотрим комбинацию доходность—риск Q. Ни один не расположенный к риску инвестор не стремился бы к позиции Q, так как он мог бы достичь той же самой доходности E[t p]q и с меньшим риском as. Q не эффективна, как и все позиции на снижающейся ветви. Следовательно, кривая эффективности, имеет во всей области определения положительный наклон. Для обоснования строгой выпуклости вверх кривой эффективности проверим, может ли она быть выпуклой вниз или линейной. Если нам удастся исключить эти два вида прохождения, то должна иметь место выпуклость вверх. [c.159]
Прямая линия пересекает ось абсцисс при а[г] = 0.08, что мы можем легко проверить за счет приравнивания к нулю предыдущего уравнения. Для определения структуры принадлежащего портфеля мы приравниваем (4.12) к нулю и выражаем через структурную переменную с результатом и = — 1. Инвесторы считаются лишь с продажей без покрытия титула 4, так как продажа без покрытия акции 6 приведет к неэффективным комбинациям доходность—риск . Кривая эффективности характеризуется уравнением [c.162]
Еще одним подходом в рамках технического анализа ценных бумаг является графический анализ. В рамках этого подхода реализуется оптимизация инвестиционного портфеля сточки зрения доходности и риска. Множество портфелей с различным соотношением риска и доходности, помечаемые на графике образуют кривую эффективных портфелей. Тангенс угла, образуемого касательной к линии эффективных портфелей, в точке касания отмечает структуру портфеля, обеспечивающего наилучшее соотношение между приростом доходности и возрастанием риска. Максимизирую функцию, определяющую тангенс указанного угла, можно найти оптимальную структуру портфеля. [c.317]
ЕСЛИ бы инвестор мог оценивать средние значения доходности и формировать дисперсионно-ковариационную матрицу для этих доходов по всем видам ценных бумаг на рынке, он мог бы создавать эффективный набор из этих видов ценных бумаг. При допущении возможности свободного от риска получения кредитов или предоставления займов на рынке инвестор смог бы определять единственный портфель на кривой эффективного множества портфелей, который имеет такие же характеристики риска-доходности, как и линия рынка капитала (это портфель, находящийся в точке касания линии рынка капитала с кривой эффективного множества). [c.168]
Сэ — эффективная выпуклость облигации V0 — начальная рыночная стоимость облигации V+(V) — стоимость облигации при параллельном сдвиге кривой рыночных доходностей на величину Лу (-Ау). [c.198]
Расположение эффективного множества на графике определяется требованиями, сформулированными в теореме о нем. Из приведенного графика видно, что портфель с минимальным уровнем риска расположен в точке Г (ни одна из точек допустимого множества не лежит вне точки Г) портфель с максимальным уровнем риска расположен в точке Б (ни одна из точек допустимого множества не лежит правее точки Б). Следовательно, множество портфелей, обеспечивающих максимальное значение уровня ожидаемой доходности в диапазон изменяющихся уровней их рисков, должно быть расположено на кривой между точками Г и Б (т.е. на верхней границе допустимого мно- [c.354]
Для инвестиций в более поздние этапы характерен более низкий коэффициент доходности капиталовложений, но ниже и степень риска. Поэтому, чем ближе инвестор к финансированию нулевой и ранней стадии образующихся компаний, тем выше ожидаемые доходы, но также и значительно выше стандарт ные отклонения от них. Если бы рынки были действующими и эффективными, то следовало бы определить, что собой представляет кривая рынка долгосрочного ссудного капитала во времени. Можно ожидать, что соотношение различных капиталовложений сместятся при изменении ситуации. На основе имеющихся данных возможно отчетливо представить, как распределяются доходы и риск по промышленным группам (рис.8). Однако в настоящее время полной и эффективной информационной системы не существует. [c.129]
Такая структура открывает больший простор для эффективного управления и портфель может выполнять предначертанные задачи, даже если за первые 5 лет он не подвергнется обновлению. Так что чисто теоретически организация, финансирующая пенсионный фонд, имеет возможность первые 5 лет погашать пенсионные обязательства и ни о чем не беспокоиться. Если процентные ставки не выскочат за пределы достаточно широко обозначенного диапазона, даже при полной пассивности менеджеров портфеля в первые 5 лет кривая доходности активов останется выше кривой пассивов. [c.459]
Функция кривой эффективной доходности возрастает и стремится к своему предельному значению доходности, которое является максимальным для данного сегмента финансового рынка. Естественно, такое значение не остается постоянным и также меняется со временем. Это свойство кривой эффективной доходности тесно связано с другим, не менее важным при увеличении срока заимствования премия за каждую дополнительную единицу времени инвестирования постоянно уменьшается, постепенно приближаясь к 0. Эта особенность объясняется слабой чувствительностью инвесторов к изменению срока инвестиций при достаточно значительном сроке и полной нечувствительностью после того, как этот срок перешагнул за границу разумного инвестирования topt. [c.225]
Целью современной теории портфеля является разработка методов, с помощью которых инвестор может выбрать оптимальный для себя портфель из бесконечного числа возможных. Для решения вопроса о включении каждой рассматриваемой ценной бумаги в портфель инвестору нужно оценить ее ожидаемую доходность и стандартное отклонение вместе со всеми ковариациями между этими ценными бумагами. Используя такие оценки, инвестор может определить кривую эффективного множества Мар-ковица. После этого для данной безрисковой ставки инвестор может найти касательный портфель и определить положение линейного эффективного множества. Наконец, инвестор может произвести инвестицию в этот касательный портфель и сделать заем или выдать кредит по безрисковой ставке. При этом сумма займа или кредита зависит от предпочтений инвестора относительно соотношения риска и доходности. [c.289]
Задача определения кривой эффективного множества Марковица может быть сильно упрощена с помощью введения процесса формирования дохода (return generating pro ess). Процессом формирования дохода называется статистическая модель, которая описывает, как образуется доход по ценной бумаге. В гл. 8 был рассмотрен один из таких процессов, известный как рыночная модель. Согласно рыночной модели, доходность по ценной бумаге является функцией доходности по индексу рынка. Однако существует много других типов процессов формирования дохода по ценным бумагам. [c.289]
Как и в случае однофакторной модели, после того, как ожидаемые доходности, дисперсии и ковариации рассчитаны с помощью приведенных выше уравнений, инвестор может перейти к использованию оптимизатора (optimizer) (особого вида математической процедуры) для получения кривой эффективного множества Марковица. Затем для данной безрисковой ставки может быть определен касательный портфель, после чего инвестор может выбрать свой оптимальный портфель. [c.297]
В общем, в то время как в двухфакторной модели для каждой ценной бумаги нужно оценить четыре параметра (а., Ьп, Ь.2 и aej), в двухсекторной факторной модели нужно оценить лишь три параметра (я(., ае. и либо Ьп, либо Ьа). Имея эти оценки вместе с оценками для FV F2, ал и ал, инвестор может применить уравнения (1 1.8) и (11.9) для расчета ожидаемых доходностей и дисперсий для каждой ценной бумаги. Парные ковариации могут быть оценены с помощью уравнения (11.10). Это даст инвестору возможность определить кривую эффективного множества Марковица, а затем касательный портфель для заданной безрисковой ставки. [c.299]
Давайте сначала исследуем возможность выпуклой вниз кривой эффективности. Эта возможность изображена в правой части рис. 4.7. Здесь мы можем составить портфели из позиций L и N. Как мы знаем из теории портфеля, эти.позиции в наихудшем случае имеют коэффициент корреляции +1. Тогда все смеси можно изобразить в виде линейной комбинации N и L. Почему здесь речь идет о наихудшем случае, мы можем себе легко уяЧяштъ, если исходя из N составим смесь из обеих позиций. Рост доходности ДЕ(г], [c.159]
ЭФФЕКТИВНЫЙ ПОРТФЕЛЬ [effi ient portfolio] — портфель, лежащий на кривой эффективного множества, обеспечивающий достижение наивысшей доходности при заданном уровне риска или наименьшего уровня риска при заданной доходности. [c.458]
Хотя построение кривых безразличия значительно сужает возможное поле формирования инвестиционного портфеля, оно не дает возможности избрать наиболее эффективный его вариант, т.к. существует множество таких вариантов, соответствующих предпочтениям конкретного инвестора. Приблизиться к решению этой задачи позволяет сформулированная П.Марковичем теорема об эффективном множестве" [effi ient set theorem]. Она фиксирует модель инвестиционного поведения инвестора в процессе формирования портфеля следующим образом Инвестор выбирает свой оптимальный вариант портфеля из их множества, каждый из которых 1) обеспечивает максимальное значение уровня ожидаемой доходности при любом определенном уровне риска 2) обеспечивает минимальное значение уровня риска при любом определенном уровне ожидаемой доходнос- [c.353]
Прямая линия соединяющая точку F любой точкой кривой, соединяющей точки R и S, представляет соЬои график описывающий соотношение риск/доходность для всех комбинаций следующих трех активов. рискованных активов 1 и 2 с безрисковыми активами. Наибольшие значение этого соотношения, которого мы можем достичь, находится на линии, соединяющей точки F и Т. Точка Т является общей точкой прямой линии, выходящей из точки F, и кривой, соединяющей точки R и S. Мы называем такой рискованный портфель, который соответствует общей точке Г на рис. 12.4, оптимальной комбинацией рискованных активов. Именно объединением этого портфеля рискованных активов с безрисковым активом достигается формирование максимально эффективного портфеля. Формула для определения долей портфеля в точке Г такова. [Е (г, ) - rf ] а - [Е (г, )-rf] pap2 [c.221]
Граница эффективного множества портфелей портфелей (effi ient portfolio frontier) — кривая, точки которой соответствуют наилучшей комбинации риска и доходности портфеля ценных бумаг, т.е. это множество эффективных портфелей. [c.324]
Это важнейшее свойство рыночных временных рядов легло в основу теории "эффективного" рынка, изложенной в диссертации Луи де Башелье (L.Ba helier) в 1900 г. Согласно этой доктрине, инвестор может надеяться лишь на среднюю доходность рынка, оцениваемую с помощью индексов, таких как Dow Jones или S P500 для Нью-Йоркской биржи. Всякий же спекулятивный доход носит случайный характер и подобен азартной игре на деньги. В основе непредсказуемости рыночных кривых лежит та же причина, по которой деньги редко валяются на земле в людных местах слишком много желающих их поднять. [c.147]
Эффективная граница - это кривая на графике, где риск портфеля (стандартное отклонение) откладывается по горизонтальной оси, а ожидаемая доходность - по вертикальной. Эффективная граница направлена вверх и вправо, что отражает увеличение риска при росте доходности. Фирма Powers Resear h сначала разработала набор оптимизированных портфелей с использованием только акций и облигаций. Построение эффективной границы производилось через определение максимальной ожидаемой доходности для каждого уровня риска. После создания оптимальных портфелей с использованием только акций и облигаций, аналогичная задача была решена для портфелей, включающих товарные фьючерсы в трех разных пропорциях. В результате получилось четыре портфеля один без товаров и еще три с содержанием 10%, 20% и 30% товарных активов. Рисунок 12.11 демонстрирует результаты включения в портфель товаров в указанных соотношениях. [c.243]
