| Рис. 2. Анализ чувствительности оптимального решения к изме- | 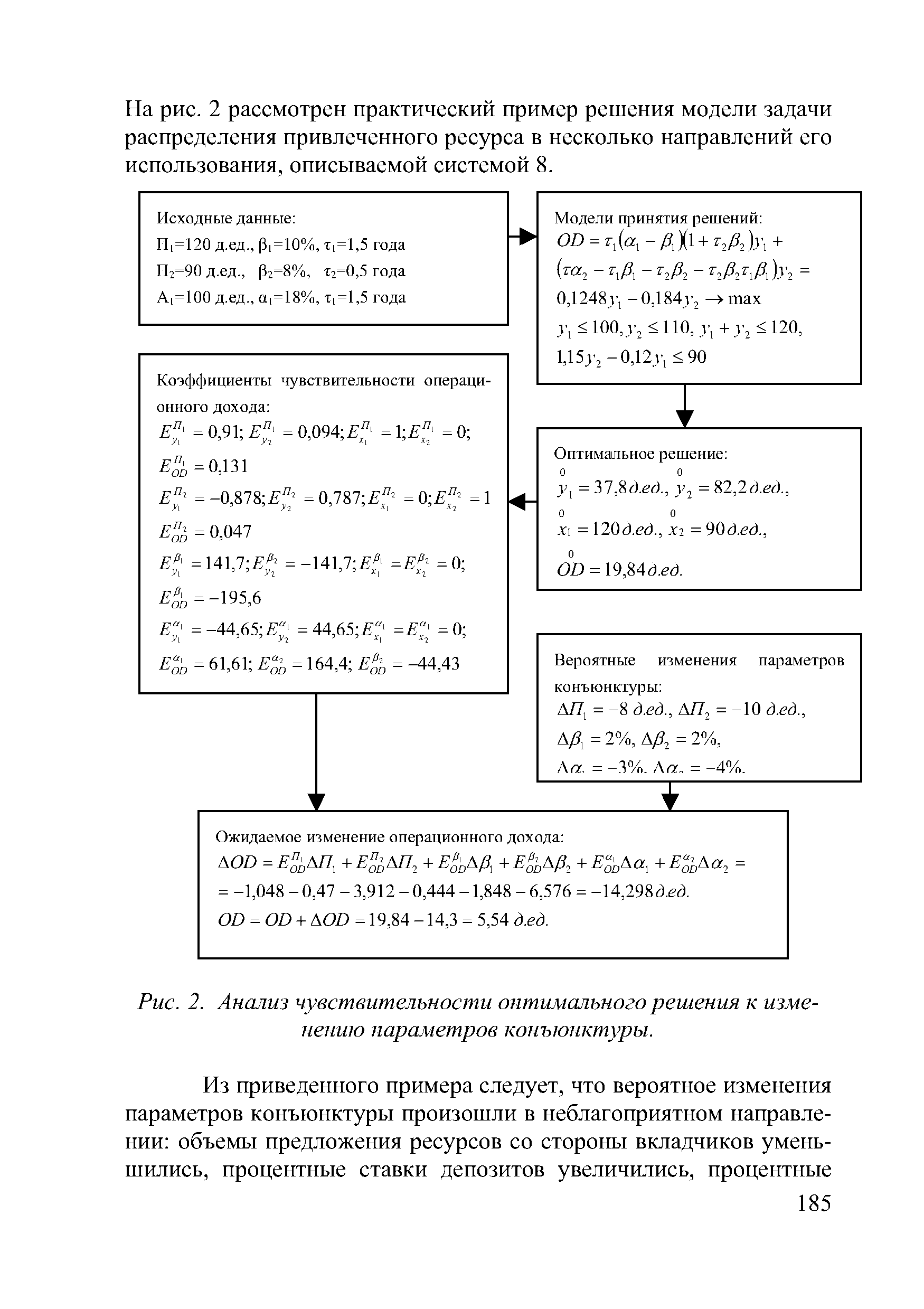 |
Члены (элементы) последовательности 269 Чувствительность оптимального решения [c.496]
Рассмотрим теперь вопрос об оценке чувствительности оптимального решения к возможной неточности исходной информации относительно коэффициентов вектора выпуска р ,..., р ..., рп. [c.120]
С помощью оценок Ду определяется близость отвергнутых вариантов к области оптимума и, следовательно, может быть оценена чувствительность оптимального решения к возможной неточности исходной информации, касающейся вектора выпуска. [c.121]
Анализ моделей на чувствительность - это процесс, реализуемый после получения оптимального решения. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели. В задаче об ассортименте продукции (пример 7.2) может представлять интерес вопрос о том, как повлияет на оптимальное решение увеличение и уменьшение спроса на продукцию или запасов исходного сырья. Возможно, также потребуется анализ влияния рыночных цен на оптимальное решение. [c.208]
Анализ на чувствительность оптимального решения к вариации коэффициентов целевой функции. В подразд. 7.4 на основе графического представления модели было показано, что при определенных значениях изменения коэффициентов целевой функции оптимальные значения переменных остаются неизменными (хотя оптимальное значение Z при этом меняется). Возвращаясь к этому вопросу, покажем, каким образом интересующую нас информацию можно [c.234]
Анализ на чувствительность оптимального решения базируется на следующих свойствах двойственных оценок. [c.247]
Задачи анализа на чувствительность оптимального решения 247 [c.425]
Чувствительность оптимального решения к изменениям ограничений задачи — степень изменения целевой функции в результате небольших изменений параметров (констант) ограничений в линейном программировании показателями чувствительности являются оптимальные оценки. В случае, когда оптимальная оценка равна нулю, оптимальное решение не зависит от соответствующего параметра ограничений. Например, если имеется избыток какого-то ресурса, то оптимальное решение не зависит от малых изменений общего объема предложения этого ресурса, т. к. оно заведомо превышает ту потребность, которая соответствует его использованию в оптимальном плане. Именно по этому оценка такого ресурса равна нулю (нулевая оценка). [c.226]
Перечислите виды всех ресурсов и ограничений задачи. Проведите анализ чувствительности оптимального решения для ресурсов (1), (2), (3) и цен q и С2 (табл. 3.2). [c.55]
Некоторая фирма производит продукцию двух видов с использованием трех видов ресурсов- неравенства (1), (3), (5). Неравенства (2) и (4) ограничивают соответственно минимальный суточный спрос на продукцию первого вида и максимальный суточный спрос на продукцию второго вида. ЦФ представляет собой доход от реализации продукции. Перечислите виды всех ресурсов и ограничений задачи и проведите полный анализ чувствительности оптимального решения (табл. 3.3). [c.56]
Перечислите виды всех ресурсов и ограничений задачи. Проведите полный анализ чувствительности оптимального решения (табл. 3.4). [c.57]
Календарные планы и методы их расчета. Распределение ресурсов в сетевых графиках проекта. Ограниченные ресурсы. Анализ ресурсной реализуемости проекта. Контроль потребности в ресурсах. Управление загрузкой ресурсов. Выравнивание загрузки ресурсов. Комплексное управление работами исполнителей. Приведение параметров календарного плана в соответствие с заданными ограничениями. Эвристические методы. Оптимальные решения. Методы анализа риска и неопределенности.. Методы снижения риска. Анализ чувствительности. Проверка [c.447]
Заключение. Использование в математической модели случайных или неопределенных факторов в значительной степени усложняет ее анализ. Поэтому исследователь всякий раз должен внимательно взвесить все обстоятельства, прежде чем включить в модель фактор такого типа. К сожалению, нельзя сформулировать строгие принципы, на основе которых можно было бы всегда решить вопрос о том, должны ли быть в некоторой модели случайные или неопределенные параметры и переменные. В некоторых случаях могут помочь методы анализа чувствительности решения по отношению к изменениям неопределенных факторов, т. е. нахождение решения задач при разных значениях неопределенных параметров и оценка того, существенно ли изменится оптимальное решение. [c.160]
Задачи анализа оптимального решения на чувствительность [c.41]
Для Л П-задач характерна высокая чувствительность решения к малым изменениям параметров. Малые изменения параметров приводят к огромным изменениям в наборе оптимальных переменных решения. При этом значения целевой функции, отвечающие этим различным оптимальным решениям, различаются очень незначительно. Это означает, что для ЛП-моделей, существует, как правило, множество альтернативных, близких к оптимальному решений. [c.87]
Основы анализа на чувствительность (анализ модели после нахождения оптимального решения) [c.443]
После того как оптимальное решение получено, выявляется его чувствительность к определенным изменениям исходной модели. В нашей задаче, например, могут представить интерес вопросы о том, как повлияют на оптимальное решение изменение запасов сырья и изменение прибыли от единицы продукции. [c.443]
Чувствительность оптимального плана к вариациям коэффициентов целевой функции. Так как любые изменения коэффициентов целевой функции оказывают влияние на симплексные разности, то такие изменения могут сделать полученное решение неоптимальным. Предположим, что коэффициент С изменился на , а коэффициент i остался без изменения, т.е. [c.451]
Обратимся к конкретной задаче и проиллюстрируем применение анализа оптимального решения на чувствительность на примере задачи оптимизации ассортимента выпускаемой продукции (пример 7.2). [c.248]
Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение задачи ЛП. [c.41]
Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в табл. 3.1. [c.49]
Используя конкретные примеры моделей задач, сформулируйте задачи, правила, экономическую интерпретацию анализа оптимального решения на чувствительность для следующих случаев [c.56]
Алгоритм не гарантирует оптимальности решения исходной задачи, но для полученного С не существует решения с лучшим значением целевой функции. Очень легко исследовать чувствительность к ограничению — достаточно его несколько ослабить и посмотреть получаемые значения целевой функции для нужных контрольных точек. [c.339]
В этих условиях руководитель предприятия не может рассчитывать только на свою интуицию. Управленческие решения и действия сегодня должны быть основаны на точных расчетах, глубоком и всестороннем экономическом анализе. Они должны быть научно обоснованными, мотивированными, оптимальными. Ни одно организационное, техническое и технологическое мероприятие не должно осуществляться до тех пор, пока не обоснована его экономическая целесообразность. Недооценка роли АХД, ошибки в планах и управленческих действиях в современных условиях приносят чувствительные потери. И наоборот, те предприятия, на которых серьезно относятся к АХД, имеют хорошие результаты, высокую экономическую эффективность. [c.19]
Предположим, что компания хочет рассмотреть различные варианты принятия решений на основании альтернативных сценариев продаж. Чтобы определить оптимальное финансирование, менеджеры могут включить в модель часть решающих правил и провести анализ "что-если" или анализ чувствительности. [c.302]
Например, при тенденции роста целесообразно открывать длинную позицию в момент, когда цены незначительно падают, приближаясь к уровню поддержки. Но где находятся эти скрытые уровни поддержки Их местонахождение нам и показывает пункто-цифровой график, причем с точностью недостижимой для столбикового. При восходящей тенденции любое промежуточное падение цен упирается в предыдущие области застоя, которые в данном случае служат областями поддержки. При нисходящей тенденции застойные области оказывают сопротивление росту цен в периоды оживления. С помощью пункто-цифрового графика значительно легче определить оптимальные моменты для урегулирования позиций. На рис. 11.5-11.8 мы наблюдаем внутридневную динамику очень короткой протяженности (от одного до девяти дней). Такие чувствительные инструменты анализа незаменимы, когда, приняв принципиальное решение, необходимо найти наиболее удачный момент для входа в рынок или выхода из него. Обладая средствами микроскопического анализа, которые предлагает пункто-цифровой график, можно кардинальным образом улучшить доходность своих операций на рынке. [c.303]
Эти исследования стали благодатной почвой для многих новаторских подходов, ищущих способы, при которых рациональное поведение могло бы привести к практически оптимальным рыночным системам. Еще одним важным шагом стало введение понятия так называемой "информационной асимметрии", описывающего ситуации, в которых участники сделки владеют разными объемами информации. Теория "асимметричной информации", т.е. ситуации, когда люди не равны в отношении качества и объема информации, используемой ими для принятия решений, расцвела в 70-ые годы в качестве объяснения поведения финансовых рынков, которые действительно чрезвычайно чувствительны к информационным трудностям. [c.98]
Можно показать, что при оптимальном размере заказа издержки на хранение равны издержкам на размещение заказа (подставив в формулу ТС найденное значение оптимального размера заказа). На практике так можно проверить правильность найденного решения. Поскольку чувствительность суммарных издержек к изменению размера заказа вблизи точки оптимума невелика, на практике размер заказа обычно округляют в большую или меньшую сторону (например, если расчеты показывают, что оптимальный размер заказа — 196,4 кг, то на практике размер заказа может оказаться равным 200 кг). [c.261]
Графический блок дает возможность с помощью средств деловой графики строить диаграммы, которые позволяют принимать организационные и финансовые решения с учетом анализа чувствительности таких важных переменных величин, как цена продаж, объем производства и реализации, величина, издержек и т. д. Целью проведения экономического анализа является также желание найти действительный результат реализации проекта в условиях конкретной национальной (региональной) экономики и принятия оптимального инвестиционного решения на весь период его реализации. [c.367]
ДОПОЛНЯЮЩАЯ НЕЖЕСТКОСТЬ [ omplementary sla kness] — термин математического программирования. (См. Жесткость и нежесткостъ ограничений ЛП.) Выполнение т.н. условий Д.н. определяет нахождение совместного оптимального решения сопряженных прямой и двойственной задач. Эти условия используются при анализе чувствительности оптимального решения к изменениям в исходных данных задачи и представляют собой один из способов формулирования Куна—Таккера условий. [c.94]
Перед тем, как переходить к практич. применению результатов операц. исследования, необходимо выяснить, насколько точно отражает модель явление, и провести анализ качества полученного решения. Адекватность модели можно проверить, сопоставляя решения, полученные на основе модели, с решениями, к-рые вырабатывались без её использования. Такое сопоставление осуществляется либо по данным о прошлом процесса, либо непосредств. практич. испытанием модели. Очень важно проанализировать чувствительность оптимального решения к изменениям значений параметров модели. Решения, очень чувствительные к таким изменениям, вызывают, как правило, определ. недоверие, поскольку в большинстве случаев параметры модели не могут быть точно измерены. Во мн. случаях качество операц. модели определяется её согласованностью с существующей структурой организации управления, в частности тем, насколько она увязана с информац., командно-распорядит. и регулирующей подсистемами организации. В случае, если модель по тем или иным соображениям представляется неудовлетворительной, она корректируется и уточняется. Поскольку модели И. о. по преимуществу используются неоднократно, корректироваться могут и уже успешно используемые модели, если в процессе их практической эксплуатации , по мере накопления опыта, выясняются новые обстоятельства, к-рые могут уточнить модель. [c.74]
АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ОДНОИНДЕКСНЫХ ЗАДА ЧЛП [c.41]
Проанализируем чувствительность оптимального решения задачи № 1.01 о производстве красок. ОДР задачи № 1.01 (рис. 3.1)- многоугольник AB DEF. В оптимальной точке Е пересекаются прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ресурсы (ингредиенты А и В) - дефицитными. [c.43]
Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Связывающие ограничения проходят через оптимальную точку. Несвязывающие ограничения не проходят через оптимальную точку. Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представляемый несвязывающим ограничением — недефицитным. Ограничение называют избыточным в том случае, если его исключение не влияет на ОДР и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность. [c.41]
При наличии гетерогенной пространственной плотности вероятности искр р, ясно, что плотность г пожарных заслонов пространственно не должна быть однородна большее количество заслонов необходимо в чувствительных зонах, где искры более многочисленны. Плотность г заслонов не будет, таким образом, постоянна в оптимизационном процессе, но будет приспосабливаться к предопределенному распределению искр р. Это пространственное распределение искр р определяет вероятность р,- того, что искра зажжет пожар в данной области или кластере /, офаниченном пожарной стеной р, является суммой р в кластере. При неоднородном распределении искр, можно показать [71,394], что оптимизация продуктивности, то есть минимизация среднего размера пожара, с учетом стоимости пожарной стены, ведет к степенному распределению областей, разфаниченных заслонами. Процесс оптимизации обеспечивает устойчивые результаты, несмотря на неопределенность, количественно определяемую вероятностями р,. В примере для лесного пожара, оптимальное пространственное распределение заслонов является результатом взаимодействия между нашим априорным знанием неопределенности в распределении искр и убытков, вызванных пожарами. Решения устойчивы относительно существования неопределенности, то есть к тому факту, что мы детерминировано не знаем куда искры собираются упасть мы знаем только их распределение вероятности. [c.375]
