Научно обоснованным способом взвешивания достоинств исходных точек для вычисления прогнозируемых значений является алгоритм экспоненциальной средней, по которому значения весов х, по мере отдаления предшествующей точки от прогнозируемой убывают по экспоненте. [c.219]
Наиболее часто применяемыми в экономике функциями являются элементарные линейная, логарифмическая, степенная, экспонента и т.д., а также различные их комбинации (см. таблицу ниже). [c.220]
Для построения прогнозных моделей используют различные группы типичных функций, из которых выбирают характерную для исследуемого объекта. Так, в первую группу входят линейные функции, во вторую — чистые экспоненты и с насыщением, т. е. логистические или S-образные кривые, в третью — кривые, характеризующие удвоенный экспоненциальный рост с последующим насыщением, в четвертую — кривые, характеризующиеся сначала медленным, а затем резким экспоненциальным ростом с последующим насыщением. [c.23]
Для моделирования уровней процентных ставок в статистике используют различные типы уравнений, в том числе полиномы разных степеней, экспоненты, логистические кривые и прочие виды функций. [c.619]
Если преобразовать приведенную выше рекурсивную формулу в более обобщенную, подставляя в уравнение последовательно вместо У, , предыдущее уравнение с У, 2 и т.д., то можно будет заметить, что перед наблюдением у,л стоит вес а(1- а)1, перед у, 2 стоит а (1- а)2 и т.д., т. е. вес отдельного наблюдения убывает соответственно экспоненте по мере удаления наблюдения у, в прошлое. Поэтому средняя и называется экспоненциальной. Дисперсия экспоненциальной средней равна [c.665]
Курс растущий. Для аппроксимации спроса от валютного курса выбрана гипербола, а для аппроксимации предложения от валютного курса — экспонента. Тогда [c.679]
Средний темп изменения определяется наиболее точно при аналитическом выравнивании динамического ряда по экспоненте (см. п. 9.5 и 9.6). Если можно пренебречь колеблемостью, то средний [c.316]
Если k > 1, экспоненциальный тренд выражает тенденцию ускоренного и все более ускоряющегося возрастания уровней. Такой характер свойствен, например, размножению организмов при отсутствии ограничения со стороны среды кормов, пространства, хищников, болезней. При росте по экспоненте абсолютный прирост пропорционален достигнутому уровню. Так росло население Земли в эпоху демографического взрыва в XX столетии сейчас этот период заканчивается и темп роста населения стал уменьшаться. Если бы он остался на уровне 1960 - 1970 гг. т. е. около 2% прироста в год от 1985 г., когда население составило 5 млрд чел., то к 2500 г. население Земли достигло бы уровня 5 млрд 1,02515 = 134 трлн 286 млрд человек на 1 человека приходилось бы примерно 1 м2 всей площади суши. Ясно, что рост любого объекта по экспоненциальному закону может продолжаться только небольшой исторический период времени, ибо ресурсы для любого процесса развития всегда встретят ограничения. [c.324]
При < 1 экспоненциальный тренд означает тенденцию постоянно все более замедляющегося снижения уровней динамического ряда. Такая тенденция может быть присуща динамике трудоемкости продукции, удельных затрат топлива, металла на единицу полезного эффекта (на 1 кВт ч, на 1 м2 жилой площади и т.д.) при технологическом прогрессе экстремальных точек экспонента не имеет. [c.324]
Когда тип тренда установлен, необходимо вычислить оптимальные значения параметров тренда исходя из фактических уровней. Для этого обычно используют метод наименьших квадратов (МНК). Его значение уже рассмотрено в предыдущих главах учебного пособия, в данном случае оптимизация состоит в минимизации суммы квадратов отклонений фактических уровней ряда от выравненных уровней (от тренда). Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую вычисляют параметры тренда. Рассмотрим лишь три такие системы для прямой, для параболы 2-го порядка и для экспоненты. Приемы определения параметров других типов тренда рассматриваются в специальной монографической литературе. [c.329]
Нормальные уравнения МНК для экспоненты имеют следующий вид [c.330]
Вторая половина таблицы - это прогноз уровней урожайности по трем видам трендов на годы /,. = 12, 13, 14, 15 и 16 от начала отсчета (1986 г.). Прогнозируемые уровни по экспоненте вплоть до 16-го года ненамного выше, чем по прямой. Уровни тренда-параболы - снижаются, все более расходясь с другими трендами. [c.334]
Для рядов с тенденцией, близкой к экспоненте, следует рекомендовать корреляцию цепных темпов роста. Вычисление корреляции рядов динамики по цепным показателям не требует предварительного вычисления трендов, но все же желательно иметь о характере тенденции приближенное представление. Для параболических трендов с не очень большими ускорениями можно коррелировать цепные абсолютные изменения при больших ускорениях лучше их не коррелировать. Если коррелируемые ряды имеют разные типы тенденций, вполне допустимо коррелировать соответствующие разные цепные показатели абсолютные изменения в одном ряду с темпами изменений в другом и т. д. [c.366]
Развитие по экспоненте. Экспоненциальное сглаживание временных рядов - модификация метода наименьших квадратов для анализа временных рядов, при котором более поздним наблюдениям придается больший вес, иными словами, веса точек ряда убывают (экспоненциальный закон) по мере удаления в прошлое. [c.175]
Для отображения основной тенденции развития явлений во времени применяются различные уравнения, полиномы разной степени, экспоненты, логистические кривые и другие функции. [c.80]
Расчет параметров полиномов различными методами. После того как выяснен характер кривой развития, необходимо определить ее параметры. Элементарный метод определения параметра уравнения тренда, описанного полиномом или экспонентой, состоит в решении системы уравнений по известным уровням ряда динамики. Ниже приводится методология расчета параметров уравнения прямой, параболы второго порядка и экспоненты. [c.81]
При сглаживании ряда динамики по экспоненте (у, = a0e fl ) для определения параметров применяется метод наименьших квадратов к логарифмам исходных данных. Так, для нахождения параметров экспоненты необходимо решить следующую систему уравнений [c.82]
Экспонента отражает постоянный относительный рост, равный о а единицам. [c.83]
| Рис. 4.7. Трендовая модель тенденции развития рынка по экспоненте | 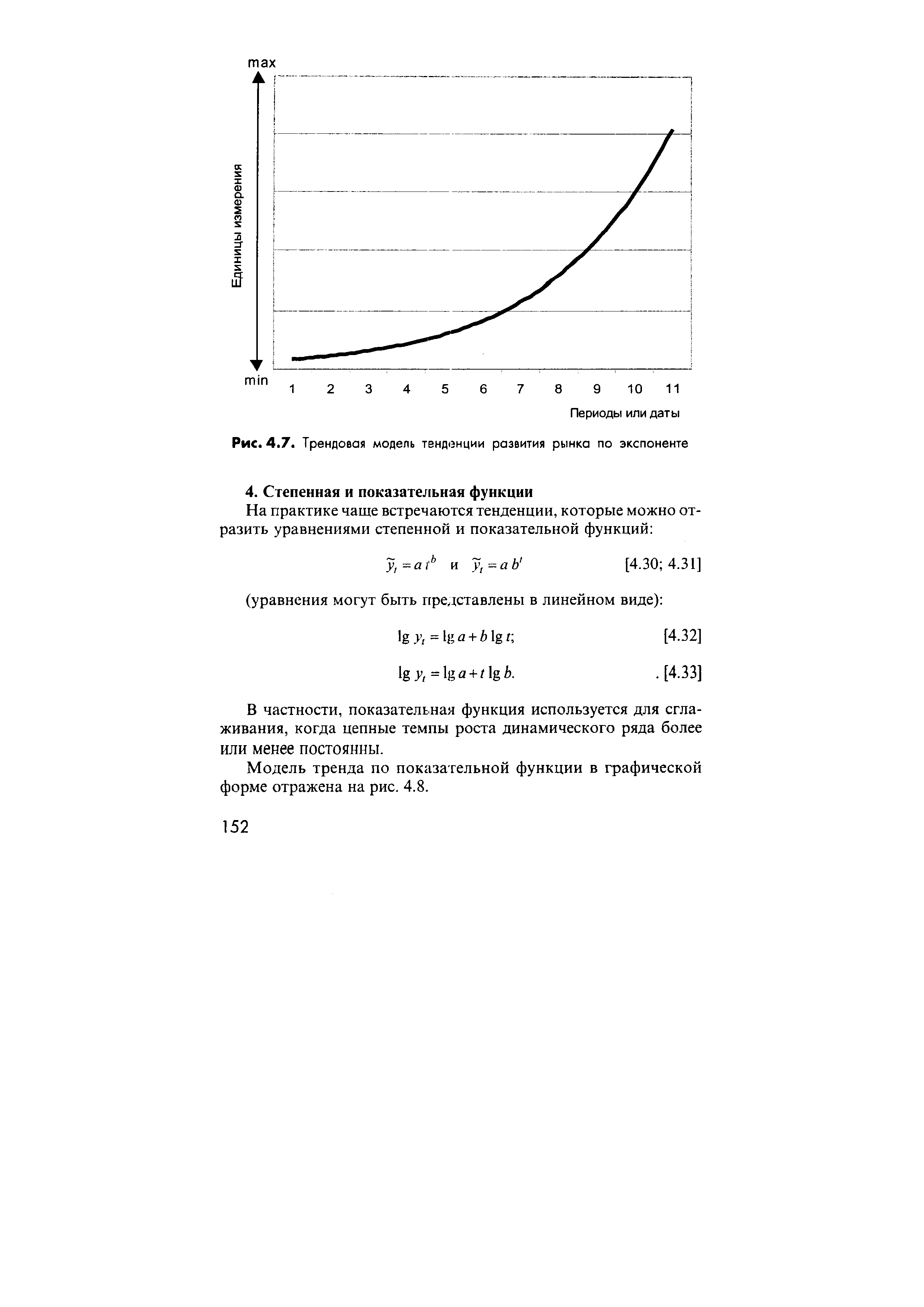 |
Наиболее часто для аналитического выравнивания применяют прямую (y=a+bt), степенную функцию (y=atb), экспоненту (у=аеы) и гиперболу [ /=а+( //)]. [c.28]
О виде кривой можно судить по характеру изменения динамического ряда во времени. Так, постоянство среднего прироста во времени характерно для прямой, линейное изменение прироста характерно для параболы второй степени, а постоянный темп роста — для экспоненты и т. д. [c.30]
При использовании методов аналитического выравнивания для прогнозирования товарооборота нефтеснабсбытовых организаций определенный интерес представляет выбор кривой и длины временного ряда. Этот вопрос исследован на основе анализа временных рядов валового товарооборота в целом по Главнефтеснабу РСФСР и его территориальным управлениям. Данные о динамике валового товарооборота Главнефтеснаба РСФСР за 15 лет (с 1960 по 1974 г.) приведены в табл. 8. Товарооборот базисного 1960 г. принят за 100%. Данные табл. 8 свидетельствуют о том, что для прогнозирования товарооборота в целом по Главнефтеснабу РСФСР предпочтительнее прямая или экспонента. [c.34]
При прогнозировании спроса на автомобильный бензин аналитическое выравнивание лучше проводить по экспоненте, а для топочного мазута — по прямой. Применение методов аналитического выравнивания для планирования реализации топочного мазута может иметь лишь ограниченный характер. Из данных табл. 9 видно, что лишь для 8. управлений из 46 коэф- фициент вариации меньше 5 %. [c.37]
Данные табл. 39 показывают, что лучшие результаты получаются при выравнивании по прямой, чем по экспоненте. В связи с небольшим периодом наблюдения данные прогноза по прямой и экспоненте незначительно отличаются между собою, однако следует предполагать, что с удлинением временного ряда показатели выравнивания по экспоненте будут ухудшаться. [c.79]
Другая тенденция заключается в том, что количество учитываемых свойств стремятся уменьшить, так как это сокращает затраты труда и времени на осуществление комплексной оценки. В некоторых случаях эти соображения имеют существенное значение, поскольку с возрастанием числа принимаемых во внимание свойств трудоемкость их учета во многих задачах, связанных с квалиметрией (например, при оптимизации качества), увеличивается по экспоненте [202—206]. Под влиянием этой тенденции в некоторых методиках оценки качества число учитываемых свойств уменьшено до предела — вплоть до того, что качество отождествляется только с одним каким-то его свойством [84—14 86—20], т. е. фактически определяется уже не качество, а главное (еди-н и ч я о е) качество. [c.103]
В. Ф. Пугачев использует для выражения функции Q(t) экспоненту вида [c.136]
При достаточно больших сроках службы изменение суммарных затрат на все виды ремонта и амортизации машины происходит по экспоненте. Это свойство суммарных затрат имеет важное практическое значение. Благодаря тому, что величина s стабилизируется, суммарная норма возмещения затрат на собственно амортизацию и ремонт агрегата может быть найдена с достаточной для практических целей точностью без определения самого срока службы агрегата. Из фиг. 83 — 84 видно, что для токарного станка ДИП-200 суммарная величина собственно амортизации и 204 [c.204]
При этом, разумеется, не исключается возможность применения и экспоненты (9). Дело в том, что несмотря на некоторые различия в структуре, функции (2), (9) почти идентичны по характеру их изменения в зависимости от величины к. Обе они могут быть динамизированы введением временного показателя t [c.138]
Рассчитанные по уравнениям трендов уровни записаны в трех последних графах табл. 9.5. Как видно по этим данным, расчетные значения уровней по всем трем видам трендов различаются ненамного, так как и ускорение параболы, и темп роста экспоненты невелики. Существенное отличие имеет парабола - рост уровней с 1995 г. прекращается, в то время как при линейном тренде уровни растут и далее, а при экспоненте их рост ускоряется. Поэтому для прогнозов на будущее эти три тренда неравноправны при экстраполяции параболы на будущие годы уровни резко разойдутся с прямой и экспонентой, что видно из табл. 9.6. В этой таблице представлена распечатка решения на ПЭВМ по программе Statgraphi s тех же трех трендов. Отличие их свободных членов от приведенных выше объясняется тем, что программа нумерует года не от середины, а от начала, так что свободные члены трендов относятся к 1986 г., для которого / = 0. Уравнение экспоненты на распечатке оставлено в логарифмированном виде. Прогноз сделан на 5 лет вперед, т.е. до 2001 г.. При изменении начала координат (отсчета времени) в уравнении параболы меняется и средний абсолютный прирост, параметр Ъ, так как в результате отрицательного ускорения [c.332]
В строке Data приводятся уровни исходного ряда Fore ast summary означает сводные данные для прогноза. В следующих строках - уравнения прямой, параболы, экспоненты - в логарифмическом виде. Графа ME означает среднее расхождение между уровнями исходного ряда и уровнями тренда (выравненными). Для прямой и параболы это расхождение всегда равно нулю. Уровни экспоненты в среднем на 0,48852 ниже уровней исходного ряда. Точное совпадение возможно, если истинный тренд - экспонента в данном случае совпадения нет, но различие, мало. Графа МАЕ -это дисперсия я2 - мера колеблемости фактических уровней относительно тренда, о чем сказано в п. 9.7. Графа МАЕ - среднее линейное отклонение уровней от тренда по модулю (см. параграф 5.8) графа МАРЕ - относительное линейное отклонение в процентах. Здесь они приведены как показатели пригодности выбранного вида тренда. Меньшую дисперсию и модуль отклонения имеет парабола она за период 1986 - 1996 гг. ближе к фактическим уровням. Но выбор типа тренда нельзя сводить лишь к этому критерию. На самом деле замедление прироста есть результат большого отрицательного отклонения, т. е. неурожая в 1996 г. [c.334]
Вид кривой жизненного цикла потребности и ее теоретическая интерпретация в каждом конкретном случае могут быть различными. Наиболее приемлемыми функциями, описывающими поведение графика потребности в этот период могут быть кривая Гомпертца и логистическая кривая. Но в отдельных случаях с достаточной степенью точности изменение потребности может быть аппроксимировано модифицированной экспонентой, логарифмической и обратнологарифмической зависимостями. При этом идентификация кривой жизненного цикла потребности по выбранной аналитической зависимости производится с использованием математического инструментария, в частности, основных положений теории математической статистики. [c.136]
Примечание. В числителе показан результат выравнивания по прямой, в менателе — по экспоненте. [c.36]
Исходя из среднегодовой величины прироста запасов в мире за период 1945—1975гг. в размере 2,3 млрд. т, начальных разведанных запасов на 01.01.1977г. 70 млрд. т и годового потребления нефти 2,3 млрд. т в работе [53] была рассчитана максимально возможная динамика добычи. При этих допущениях добыча нефти может возрасти по экспоненте лишь до 1992 г., когда спрос на нефть составит 3,9 млрд. т. После этого потребление ее будет ограничено возможным объемом добычи, равным 1/15 от уменьшающейся величины запасов R(t). Из этих [c.75]
Задаваясь некоторой динамикой прироста запасов в регионе, например падением по экспоненте с годовым темпом ф, и рассматривая процесс затрат и прироста запасов как непрерывный, получаем следующее выражение для СПЕЗ [c.108]
При анализе экономической обстановки за последние 30-40 лет можно провести три линии развития ТУ, отдача от которых в сумме дает какой-либо экономический показатель (рис. 2). Кривая Ш, показывающая развитие третьего ТУ и его вклад в воспроизводство, вырождается по линейной зависимости. Кривая IV несет основную тяжесть. Она наиболее полно отображает драматические события нашей экономики за последние десятилетия. Внедряя достижения химии и нефтехимии, ЭВМ, используя авиатранспорт и атомную энергию, в 60-х годах удалось существенно поднять благосостояние народа, затем рост замедлился и стал катастрофически падать. До фазы стабилизации мы еще не дошли. Но падение не может продолжаться бесконечно и, вероятно, в ближайшее время его удастся остановить. Пятый ТУ изображен в виде прямой линии, которая по прогнозу должна устремиться вверх по экспоненте. От момента линейной зависимости на экспоненциальную и степени крутизны зависит наше благополучие. [c.57]
Смотреть страницы где упоминается термин Экспонента
: [c.82] [c.90] [c.85] [c.252] [c.59] [c.678] [c.678] [c.80] [c.228] [c.385] [c.30] [c.36] [c.37] [c.78]Большая экономическая энциклопедия (2007) -- [ c.766 ]
