Металл пдк, мг/кг Место изготовления продукции Размер выборки Среднее значение, мг/кг Минимальное значение, мг/кг Максимальное значение, мг/кг Средне-квадратичное отклонение Критерий Стьюдента Itl [c.57]
Вычисление парных коэффициентов корреляции между исследуемыми факторами, построение уравнения регрессии, проверка его надежности по критериям Фишера и Стьюдента, исключение из исходной матрицы ненадежных факторов. [c.34]
Вопрос о случайности или неслучайности различия средних показателей работы долот при бурении с отклонителем и на прямой трубе устанавливают по критерию Стьюдента [c.58]
Из табл. 10 следует, что полученным значениям критерия Стьюдента s соответствуют вероятности более 0,90. Следовательно, условия работы турбобура при бурении вертикальных и наклонных скважин, а также при изменении диаметра скважин существенно изменяются и характеризуются различным межремонтным периодом работы. [c.61]
Следует отметить, что по элементам полученной матрицы коэффициентов парной корреляции rih можно предварительно проанализировать зависимость между производительностью труда и каждым из влияющих на нее факторов, а также между самими факторами и выделить среди них претендентов на дальнейшее исключение. Для этого в первую очередь отыскивают коэффициенты r,ft, близкие к единице и превышающие некоторое пороговое значение 6 = 0,7- 0,8. Затем все коэффициенты rik проверяют на значимость по -критерию (Стьюдента). Если при заданном значении уровня значимости q значение ь>Табличное, то гш значимо. [c.80]
Существенность включенных в уравнения регрессии (20) — (22) факторов оценена по коэффициенту множественной корреляции R и путем проверки по /-критерию Стьюдента. [c.86]
Для выявления существенности факторов х,- в уравнениях (20) — (22) были рассчитаны значения -критерия Стьюдента для всех коэффициентов уравнения регрессии, которые затем были сопоставлены с табличными значениями. Как видно из табл. 37, расчетные значения -критерия Стьюдента для всех коэффициентов полученных уравнений регрессий (20) — (22) выше табличных, что свидетельствует о их значимости. [c.86]
Коэффициент регрессии ff/= 22,4O4 этого уравнения найден с высокой точностью, превышающей табличное значение функции Стьюдента для уровня значимости 0, 9 9. Относительная погрешность приближения по этому уравнению колеблется от 0,5 до 5%. [c.50]
Отбор значимых факторов приведенных выше уравнений регрессии осуществлялся на основе применения критерия Фишера, а коэффициенты регрессии найдены с точностью, определяемой функцией Стьюдента (3). [c.54]
Управления буровых работ Количество наблюдений Коэффициент Стьюдента Общее выполнение норм времени [c.21]
Операторы 26 — 35. Проверка на возможность объединения исходных данных по типам буровых установок в одну совокупность (для построения единой модели). Производится она по критериям Фишера и Стьюдента. Условные обозначения здесь F — критерий Фишера. Критические значения Рщ, приведены в приложении (см. табл. 2) t — критерий Стьюдента. Критические значения tKp приведены в приложении (см. табл. 3). [c.71]
Операторы 89 -94. Проверка надежности коэффициентов регрессии уравнения для объединенной совокупности по критерию Стьюдента. В этой группе операторов выделяется подпрограмма вычисления средней квадратической ошибки коэффициентов регрессии (оператор 90). Алгоритм этой подпрограммы представлен на рис. 10. [c.75]
Операторы 124—136. Проверка надежности коэффициентов регрессии уравнений для каждого типа буровых установок по критерию Стьюдента. [c.75]
Значимость коэффициента корреляции может быть оценена с помощью /-критерия Стьюдента. Алгоритм расчета этого критерия при линейной однофакторной связи такой [c.76]
Значимость коэффициентов простой линейной регрессии (а и Ь) также может быть установлена с помощью /-критерия Стьюдента. Кроме того, адекватность однофакторной регрессионной модели можно оценить с помощью F-критерия Фишера, алгоритм которого выглядит таким образом [c.76]
При создании многофакторной корреляционной модели необходимо отбирать самые значимые факторы, которые оказывают решающее воздействие на результативный показатель, так как охватить все условия и обстоятельства практически невозможно. Факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет. [c.139]
Эти сведения вводятся в ПЭВМ и рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации, множественные коэффициенты корреляции и детерминации. [c.145]
Значимость коэффициентов корреляции проверяется по критерию Стьюдента [c.148]
Jn-l V40 -1 Если расчетное значение t выше табличного, то можно сделать заключение о том, что величина коэффициента корреляции является значимой. Табличные значения t находят по таблице значений критериев Стьюдента. При этом учитываются количество степеней свободы (V = п — 1)и уровень доверительной вероятности (в экономических расчетах обычно 0,05 или 0,01). В нашем примере количество степеней свободы равно п - 1 = = 40 - 1 = 39. При уровне доверительной вероятности Р = 0,05 t = 2,02. Поскольку /-фактическое (табл. 7.8) во всех случаях выше f-табличного, связь между результативным и факторными показателями является надежной, а величина коэффициентов корреляции — значимой. [c.148]
| Таблица 7.8 Фактические значения критерия Стьюдента |  |
Коэффициент / зависит от размера выборки и доверительной вероятности, его значения приведены в табл. 6.2. При больших выборках распределение Стьюдента не отличается от нормального и [c.61]
| Таблица 6.2 Коэффициенты fy доверительной вероятности Стьюдента | 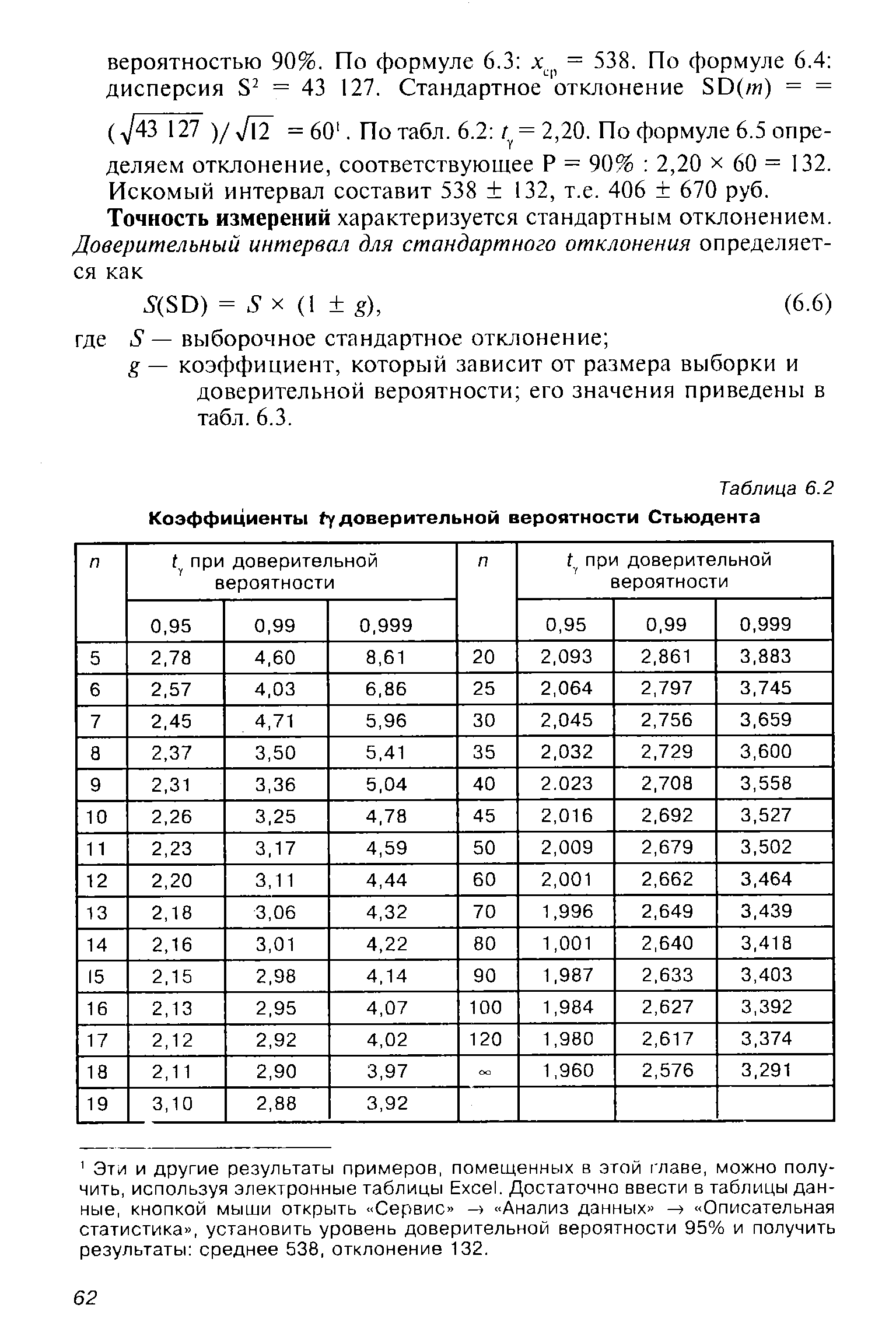 |
Значимость а, в двухфакторной модели можно оценить t-кри-терием Стьюдента [c.329]
Для оценки статистической надежности параметров уравнения регрессии рассчитаны средние ошибки оценок коэффициентов регрессии, значения /-критерия Стьюдента при 12 степенях свободы вариации [c.331]
Факторы Средние ошибки оценок коэффициентов /-критерий Стьюдента Вероятности нулевой гипотезы относительно коэффи- [c.331]
Значение -критерия Стьюдента для 23 степеней свободы (т=п- =24 - 1) с вероятностью а =0,005 равно 2,307. [c.611]
В любом случае правильность проведения типологической группировки требует проверки. С этой целью рассчитываются сводные показатели по группам (средние, относительные величины) если различие между группами статистически незначимо (по /-критерию Стьюдента или F-критерию, или критерию yj и т.д., см. гл. 7), то схема группировки должна быть пересмотрена - схожие группы могут быть объединены, изменены границы интервалов и т. д. [c.125]
Распределение Стьюдента имеет только один параметр d.f. -число степеней свободы (иногда обозначается К). [c.191]
Это распределение, как и нормальное, симметрично относительно точки / = 0, но оно более пологое. При увеличении объема выборки, а следовательно, и числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Число степеней свободы равно числу тех индивидуальных значений признаков, которыми нужно располагать для определения искомой характеристики. [c.191]
Таблицы распределения Стьюдента публикуются в двух вариантах [c.191]
Первая задача чаще всего решается при неизвестной генеральной дисперсии. Испытуемая гипотеза Н0 ц = ца, альтернативная гипотеза Н ц Ф ц0. Испытание гипотезы проводят с помощью /- критерия. При большом числе наблюдений критическое значение критерия определяется по таблице интеграла вероятностей, при малом - по таблице распределения Стьюдента с заданным уровнем значимости и числом степеней свободы, п - 1. [c.208]
Учитывая, что средние показатели работы трехшарошечных долот указанных типоразмеров характеризуются критерией Стьюдента ts с вероятностью более 0,80 можно заключить, что количество долот в обоих вариантах вполне достаточное, показатели их работы надежные, а различие между ними при бурении с отклонителем и на прямой трубе существенное и обусловлено различным условием характера их отработки. Это является следствием возникновения отклоняющей силы значительной величины, которая приводит к радиальной вибрации долота, ухудшает условия работы опоры и вооружения шарошек долот, поглощает часть вращающего момента, развиваемого турбобуром. Кроме того, при бурении наклонных скважин, особенно с отклонителем, возрастает зависание инструмента и степень неравномерной подачи его на забой, что сказывается на характере отработки долот. [c.58]
Значение критерия Стьюдента /s при числе степеней свободы Л = 25 + 28—2 = 51 составляет 2,58, которому соответствует вероятность Я>0,90. Поэтому можно считать, что средние значения проходки трехшарошечного долота Б-269С при бурении с указанными двумя отклонителями надежные, их количество достаточно, разница между ними (увеличение проходки на долото в 1,26 раза) не случайная, а существенная и обусловлена улучшением условий их отработки при использовании отклонителя с рациональным значением угла перекоса осей резьб. При этом механическая скорость проходки в среднем увеличивается в 1,11 раза. [c.184]
Значимость полученных регрессионных моделей (20) — (22) проверяли с помощью статистического критерия Фишера F, по критерию Стьюдента и по критерию аост/<т - [c.83]
Фактический уровень r-критерия Стьюдента больше соответствующего табличного значения. Поэтому нулевая гипотеза о случайном характере изменения процентных ставок финансовой компании отклоняется. Так как значение г-критерия Стыодента определено с вероятностью, равной 0,005, то можно предположить, что в пяти случаях из тысячи колебания процентных ставок носят случайный характер. [c.611]
Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить / и доверительную вероятность F(t). При п > 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < п < 100 различия незначительны. Поэтому практически к малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц). [c.190]
Выдвигается гипотеза о том, что норму выработки пересматривать не нужно, т.е. Н0 ц = 400 кг. Проверим эту гипотезу на 5%-ном уровне значимости. Критическое значение /-критерия определяется по таблице распределения Стьюдента при доверительной вероятности 0,95 (1 - 0,05) и числе степеней свободы d.f. = п - 1 = 8. Критическое значение составит (кршп= 2,3. Фактические значения /-критерия вычисляются по формуле (7.36) [c.209]
Смотреть страницы где упоминается термин Стьюдента
: [c.61] [c.177] [c.205] [c.80] [c.89] [c.26] [c.55] [c.140] [c.660] [c.192]Словарь современной экономической теории макмиллана (2003) -- [ c.0 ]
Прикладная статистика Исследование зависимостей (1985) -- [ c.380 ]
Маркетинговые исследования Издание 3 (2002) -- [ c.582 ]
