Для множества показателей, значения которых увеличиваются при улучшении показателя (например, рентабельность собственного капитала), масштабирование производится по следующей формуле [c.84]
Для множества показателей, значения которых уменьшаются при улучшении показателя (например, длительность оборота кредиторской задолженности), масштабирование производится по формуле (2) [c.85]
Влияние состава газа, характеристикой которого может служить относительная плотность газа р, учитывается только формой масштабирования давления и температуры, т. е. для нахождения приведенных термодинамических параметров газа. [c.111]
Для съема показаний и обработки диаграмм многих показывающих и самопишущих приборов нужен большой штат обслуживающего персонала. Если учесть возможные ошибки операторов при считывании показаний, обработке с целью масштабирования результатов и приведении их к единицам измеряемых величин, следует признать, что наиболее удобная форма представления информации — цифровая. Она легко поддается кодированию, а в закодированном виде данные о процессе могут поступать в ЭВМ для дальнейшей обработки. [c.210]
Пределы масштабирования изображения электронных таблиц 10-400% [c.330]
Дополнительные настройки оптимизации выполняются в диалоговом окне Параметр поиска решения. В частности, можно ограничить время выполнения поиска решения и выполнения промежуточных вычислений, максимальное время — не более 9 часов, точность, с которой найденное решение соответствует целевому значению, допустимое отклонение для переменных от оптимального значения. Для задач с нелинейной целевой функцией задается параметр сходимости, который влияет на прекращение поиска. Если относительные изменения значения целевой функции за последние пять итераций меньше указанного числа, поиск прекращается. Выполняется установка типа модели — линейная, если целевая функция линейная. Можно выводить результаты итераций, выполнять автоматическое масштабирование параметров модели. [c.457]
Рассмотрим пример. Емкостью рынка для нового ксерокса с несколько измененными основными параметрами (скорость и качество печати, возможность масштабирования и т.д.) будет количество потребителей, которым необходимо копировать документы. Если же в новом аппарате совмещены функции ксерокса и, например, факса, то он будет привлекать тех потребителей, кому необходимо как копировать, так и быстро пересылать документы. И, наконец, если ксероксу добавлены дополнительные функции возможность брошюровки, печати с большой скоростью и в больших объемах и т.д., то он уже может выступать в роли небольшой типографии и, соответственно, претендовать на свою долю данного сегмента рынка. [c.29]
Имея это в виду, вы можете использовать отдельные свечи для масштабирования действующего на рынке баланса спроса и предложения. [c.87]
Нет. Добавление к проигрышной позиции — оно и есть добавление, то есть потенциально еще большее увеличение проигрышной позиции. Бывают ситуации, когда вы решаете покупать по разным ценам или продавать по разным ценам, потому что такое "масштабирование" часть вашей стратегии и осуществляется в соответствии с вашим техническим анализом. Это совсем не то, однако, что добавление к проигрышной позиции в надежде, что рынок развернется и восполнит все ваши предыдущие убытки. Например, если вы открываете длинную позицию в акции по курсу 20 долл. за штуку, а затем она резко падает, гораздо лучше выйти на уровне заранее рассчитанного убытка и подождать по явления следующего сценария. Но если вы вместо этого решаете купить больше по цене 19,25 долл., затем 19 долл., а затем 18,50 долл., и 18 долл., и 17.50 долл... только потому, что вы думаете (надеетесь, желаете и молитесь), что рынок достиг основания, тогда вы "виновны" в добавлении к проигрышной позиции. Иногда рынок в конечном счете находит основание, и все кончается хорошо. Но гораздо больше вероятность, что рынок продолжит идти против вас, по крайней мере некоторое время, пока у вас не нарастет слишком большая позиция с плохим соотношением риск/награда и без какого-либо серьезного технического анализа в обоснование ваших сделок. [c.96]
Это правило - еще один разработанный автором инструмент - служит стандартом для классификации участков (сегментов) в пределах данной фигуры. Оно (правило) помогает объединению масштабированных ценовых фигур и определению наименования соответствующего Порядка сег-мента. По существу, все анализы начинают с объединения моноволн в поливолны, а этих поливолн в мультиволны. Но в дальнейшем становится все труднее управлять этим процессом для каждой фигуры (визуально и со структурной точки зрения), если вы не следите за уровнем Сложности каждой фигуры до и после сжатия. [c.174]
На начальном этапе изучения теории Волн Эллиота понятие сложности особо важной роли не играет, но при переходе к построению графиков и отслеживанию долгосрочных волновых фигур его значение возрастает. Умение определять уровень сложности крайне важно при работе с масштабированными фигурами одинакового Порядка. В общем случае уровень сложности волн одинаковых ступеней может отличаться лишь на единицу (более подробное рассмотрение понятия Порядка приведено ниже). [c.174]
На Рис. 23 было выполнено стандартное преобразование, при котором сжимались или растягивались абсцисса и ордината для каждой кривой таким образом, чтобы все три кривые совпали друг с другом. Если такое преобразование окажется успешным, то это будет означать, по определению, что эти три распределения идентичны. Этот факт очень полезен для понимания лежащего в основе механизма, а также для использования в будущем при оценивании риска и управлении им. Наивно было бы ожидать, что одинаковая физика применима в каждом из сферических слоев и что, как следствие, распределения должны быть одинаковыми, если не изменять единицу длины различных масштабов, существующих в каждом слое. Здесь, мы наблюдаем, что три кривые действительно замечательно совпадают, но только для маленьких флуктуации скорости, в то время как большие колебания описываются очень разными толстыми хвостами. В противном случае, если попытаться свести кривые в области больших колебаний скорости, тогда части кривых, близких к началу (в области малых скоростей) не сходятся вообще и очень различны. Отсюда можно сделать заключение -распределения приращений скорости, по-видимому, состоят из двух областей области, так называемых "нормального масштабирования" и области экстремальных событий. [c.69]
| Рис. 90. Геометрическая спираль, показывающая две особые траектории (непрерывная и пунктирная линии) на плоскости "сниженная цена" - "скорость" (yi, /2), которая точно соединяет начало yi=0, ys=0 с бесконечностью, Эта спиралевидная структура, которая демонстрирует свойства масштабирования или фрактальные свойства, находится в начале усиливающихся осцилляции, декорирующих поведение степенной зависимости вблизи сингулярности конечного времени. Различные отрезки кривых и областей, указанные стрелками, отображены из одного в другой сквозь динамику модели. Источник [205]. | ![Рис. 90. Геометрическая спираль, показывающая две особые траектории (непрерывная и пунктирная линии) на плоскости "<a href="/info/78047">сниженная цена</a>" - "скорость" (yi, /2), которая точно соединяет начало yi=0, ys=0 с бесконечностью, Эта спиралевидная структура, которая демонстрирует свойства масштабирования или фрактальные свойства, находится в начале усиливающихся осцилляции, декорирующих поведение степенной зависимости вблизи сингулярности конечного времени. Различные отрезки кривых и областей, указанные стрелками, отображены из одного в другой сквозь динамику модели. Источник [205].](/pic1/174223118025208235063123018162224175001095117230.png) |
Рис. 105. Доллар США, выраженный в немецких марках DEM (верхняя кривая) и в швейцарских франках HF (нижняя кривая) до его обвала в середине 1985 года. Соответствие для немецкой валюты против доллара США уравнению (15) показано непрерывной плавной линией и дает Af=3.88, Bf-1.2, В ОЩ трФ.28, f =7985.20, ю 6Д и <р --12. Соответствие для швейцарской валюты против доллара США уравнению (15) дает А 3.1, Bf=-0.86, В =0.05, тяО.36, t 1985.19 оя=5.2, и | |
![Рис. 105. Доллар США, выраженный в немецких марках DEM (верхняя кривая) и в швейцарских франках HF (нижняя кривая) до его обвала в середине 1985 года. Соответствие для немецкой валюты против доллара США уравнению (15) показано непрерывной плавной линией и дает Af=3.88, Bf-1.2, В ОЩ трФ.28, f =7985.20, ю 6Д и <р --12. Соответствие для швейцарской валюты против доллара США уравнению (15) дает А 3.1, Bf=-0.86, В =0.05, тяО.36, t 1985.19 оя=5.2, и <fK-0.59. Обратите внимание на небольшие колебания значения коэффициента масштабирования 2.2< Л<2.7, которые являются одним из ключевых тестов нашей теории "критического стадного поведения". Источник [212].](/pic1/079055092254082018036185145051014137029006056147.png) |
Априорные ограничения накладываются на значения параметров, чтобы обеспечить их достоверность. Значение экспоненты ft должно находится в интервале от 0 до 1, чтобы цена увеличивалась и оставалась конечной. Более узкий диапазон 0,2< / <0,8 представляется еще более предпочтительным, для того чтобы избежать осложнений, связанных с конечными точками интервала 0 и 1. Вспомним, что угловая логопериодическая частота to определяет коэффициент масштабирования X последовательных временных интервалов между локальными максимумами через следующее отношение %=е ш. Опыт, накопленный в различных отраслях, а также некоторые теоретические аргументы говорят о том, что коэффициент А должен, как правило, находиться в диапазоне 2-3. На практике же, мы использовали ограничения 5
Зная, что многие поставщики данных не имеют в своих программах построения графиков функции постоянного масштаба, нами так разработано программное обеспечение, чтобы пользователи могли выбирать или полноэкранное масштабирование самых последних загруженных данных или постоянный масштаб от самого высокого максимума до самого низкого минимума всего ряда данных для инвесторов, испытывающих неудобство из-за необходимости конвертировать данные своих рядов данных. [c.34]
На этом достаточно о технических вопросах, параметрах, масштабировании и измерениях. Пусть следующие главы будут вдохновляющими и мотивирующими. Читатели должны воспринимать результаты наших исследований не как конечные решения проблемы превращения Фибоначчи ФИ в эффективный торговый инструмент, а как многообещающую отправную точку для проверки, модификации, улучшения и применения наших инструментов Фибоначчи. Торговля по принципам Фибоначчи напоминает путешествие. Присоединяйтесь к нам в этой захватывающей поездке. [c.35]
Нынешние дерзкие планы Mi rosoft предусматривают развитие ПК с масштабированием его за рамки достигнутого любыми существующими компьютерами. Они включают в себя создание машин, способных смотреть, слушать и учиться , и программного обеспечения для устройств нового типа — персональных секретарей. Эти инициативы стали ответом Mi rosoft на вызов электронной конвергенции — внедрения электронных технологий в самые различные устройства, породившего потребность в обеспечении их взаимодействия друг с другом. Увенчаются они успехом или нет, пока неизвестно. Ясно одно связанный с ними риск необходим, чтобы не лишиться будущего в долгосрочной перспективе. [c.272]
Для оценки инвестиционной привлекательности предприятия желательно иметь интегральный показатель. Особенностью, осложняющей сведение используемых коэффициентов в единый показатель, является их несопоставимость (проценты, доли, дни), а также разнонаправленность (увеличение одних показателей в динамике свидетельствует об улучшении финансового положения предприятия, увеличение других - об ухудшении). Для приведения показателей в удобный для сравнения, анализа и дальнейшей обработки вид предлагается процедура масштабирования, которая основана на сравнительной оценке и позволяет учитывать отраслевые особенности функционирования предприятий. [c.84]
Требования к возможности функционирования программных систем в среде вычислительных сетей и на разных программно-аппаратных платформах достаточно очевидны. В этой связи для бухгалтерий с небольшим числом автоматизированных рабочих мест обычно вполне достаточно применения одноранговых сетей ПК на платформе Intel с использованием той или иной разновидности Windows. Для более крупных бухгалтерий желательны программные системы, функционирующие в сетях ПК с выделенным сервером в архитектуре клиент-сервер. И, наконец, для АИС-БУ с большим числом рабочих мест бывает актуально применение неоднородных сетей с использованием серверов на более мощных программно-аппаратных платформах. Отсюда и требования к специализированным программам, предполагающие перспективное масштабирование системы и предусматривающие возможность его функционирования на основе технологии тонкого клиента. [c.293]
Эта неправильная стратегия, известная как "усреднение" ("averaging") или масштабирование в позицию. Когда такая стратегия часть вашего плана, усреднение — прекрасный способ войти в рынок по разным ценам. Например, если вы полагаете, что рынок приближается к максимуму, можно смасшта-бироваться в короткую позицию. Если рынок устойчиво идет вверх, можно выступить нарастающим покупателем, добавляя небольшие приращения, пока вы не установите полную позицию. [c.127]
Очевидно, что по структуре троичное канторово множество геометрически идентично самому себе только при увеличении с коэффициентом 1р=У, являющимся произвольными целочисленными степенями 3. Если вы возьмете другой коэффициент увеличения, например, 1.5, то вы не сможете наложить увеличенную часть на изначальное канторово множество. Таким образом, мы должны заключить, что троичное множество Кантора не обладает свойством непрерывной масштабной инвариантности, но обладает только дискретной масштабной инвариантностью при основном коэффициенте масштабирования 3. Это свойство проявляется логопфиодическими сю1щшшциями. [c.207]
Обратите внимание, что осцилляции сложнее, нежели просто одиночная гладкая синусоидальная структура. На самом деле это отражает присутствие всех других масштабных коэффициентов 32=9, 33=27..., при которых канторово множество инвариантно. Тонкая структура, видимая на левом графике Рис. 80, является результатом суперпозиции всех чисто логопериодических осцилляции, по одному для каждого из допустимых коэффициентов масштабирования. Это похоже на аккорд, составленный путем комбинирования ряда чистых тонов различной громкости. [c.207]
Итак, мы показали, что признаком дискретной масштабной инвариантности является присутствие степенной зависимости с комплексным показателем степени, который проявляет себя в наборе данных логопериодическими осцилляциями, корректируя простое степенное масштабирование. В дополнение к существованию единственного предпочтительного коэффициента масштабирования и связанной с ним логопериодичности, обсуждавшейся до сих пор, могут существовать несколько предпочтительных коэффициентов, соответствующих нескольким наложенным друг на друга (принцип суперпозиции) логопериодичностям. Это может привести к более разнообразному поведению, такому как лог-квазипериодичность [400]. [c.208]
Предположим, что анализ некоторых данных показывает наличие логопериодических структур. Что мы можем из этого извлечь Прежде всего, как мы увидели, период логопериодичности на логарифмической шкале прямо связан с существованием предпочтительного коэффициента масштабирования. Таким образом, логопериодичность должна быть немедленно замечена и истолкована как существование множества предпочтительных характеристических масштабов, вместе формирующих геометрический ряд. .Jf, X1 1,. ..J, J ,., .,. А",... Логопериодические структуры в данных, таким образом, указывают, что система и/или подлежащие физические механизмы обладают характеристическими масштабами, каждый из которых характеризуется соответствующим размером. Это крайне интересно, поскольку существенно ограничивает лежащий в основе этого механизм. Действительно, поведения с простой степенной зависимостью обнаруживаются повсеместно, как видно из бурного роста концепций фракталов, критичности и самоорганизующейся критичности [26]. Например, степенное распределение энергии землетрясений, известное как закон Гетенберга-Рихтера, может быть получено при помощи многих различных механизмов и описано множеством моделей и, таким образом, крайне ограничено в выявлении лежащей в его основе физики (один факт, много конкурирующих объяснений). Его полезность как модельных представлений даже подвергается сомнению, что противоречит общей уверенности, свойственной многим ученым, в важности этой степенной зависимости. Напротив, присутствие логопериодических свойств учит нас тому, что существуют важные физические структуры, скрытые в полностью инвариантном описании. [c.209]
Данный раздел представляет альтернативное понимание возникновения критических точек (конечно временных сингулярностей), осложненных ускоряющимися осцилляциями. Это альтернативное понимание основывается на описании "динамической системы", в которой данные характеристики возникают динамически. Основным компонентом является сосуществование двух классов инвесторов, "фундаменталистов или стоимостных инвесторов" и инвесторов, следующих за трендом (часто называемых чартистами, техническими аналитиками или шумовыми трейдерами на жаргоне финансовой науки). Вторым важным компонентом является признание того, что оба класса инвесторов ведут себя "нелинейно". Данные два компонента порождают конечно-временную сингулярность с ускоряющимися осцилляциями. Сингулярность степенной зависимости является результатом нелинейно возрастающего темпа роста в связи со следованием тренду. Являющиеся приблизительно логопериодическими, осцилляции с замечательными свойствами масштабирования происходят. от нелинейной возвращающей силы, с помощью которой фундаментальные инвесторы, стремящиеся вернуть цену к ее фундаментальной стоимости, влияют на нее. Можно наблюдать богатое разнообразие поведений как функции степени нелинейности темпов роста и восстанавливающей силы. Мы увидим, что динамическое поведение прослеживается назад к самоподобной спиральной структуре динамики (цены, ценовых изменений) в пространственном представлении, разворачивающейся вокруг центральной фиксированной точки [205]. [c.217]
Как показано в главе 6, логопериодическая коррекция для масштабирования подразумевает существование ифархии характеристических временных интервалов t -tn, заданных выражением (11) с предпочтительным масштабным коэффициентом, обозначенным как g или Я. Мы вычислили, что для краха в октябре 1987 года Я 1.5-1.7 (интересно, что это значение универсально и, как мы увидим, почти одинаково и для остальных крахов). Мы ожидаем, что будет происходить уменьшение показателя на краткосрочных масштабах (напримф, несколько больших, чем и), а также на долгосрочных временных масштабах, что объясняется существованием эффекта конечного размера. Эти временные масштабы tf-tn не универсальны и их значение зависит от специфики рынка. Что предполагается универсальным, так это [c.231]
| Рис. 102. Спектральный анализ Ломба для трех пузырей, предшествующих обвалам на фондовом рынке Гонконга (Рис. 99 - Рис. 101). См. раздел "Непараметрический тест логопериодичности" далее в этой главе. Всем трем пузырям свойственна практически одинаковая "универсальная" логочастота f==1, относящаяся к предпочтительному коэффициенту масштабирования дискретной инвариантности шкалы, равного Д=exp(r/f) =2/7. |  |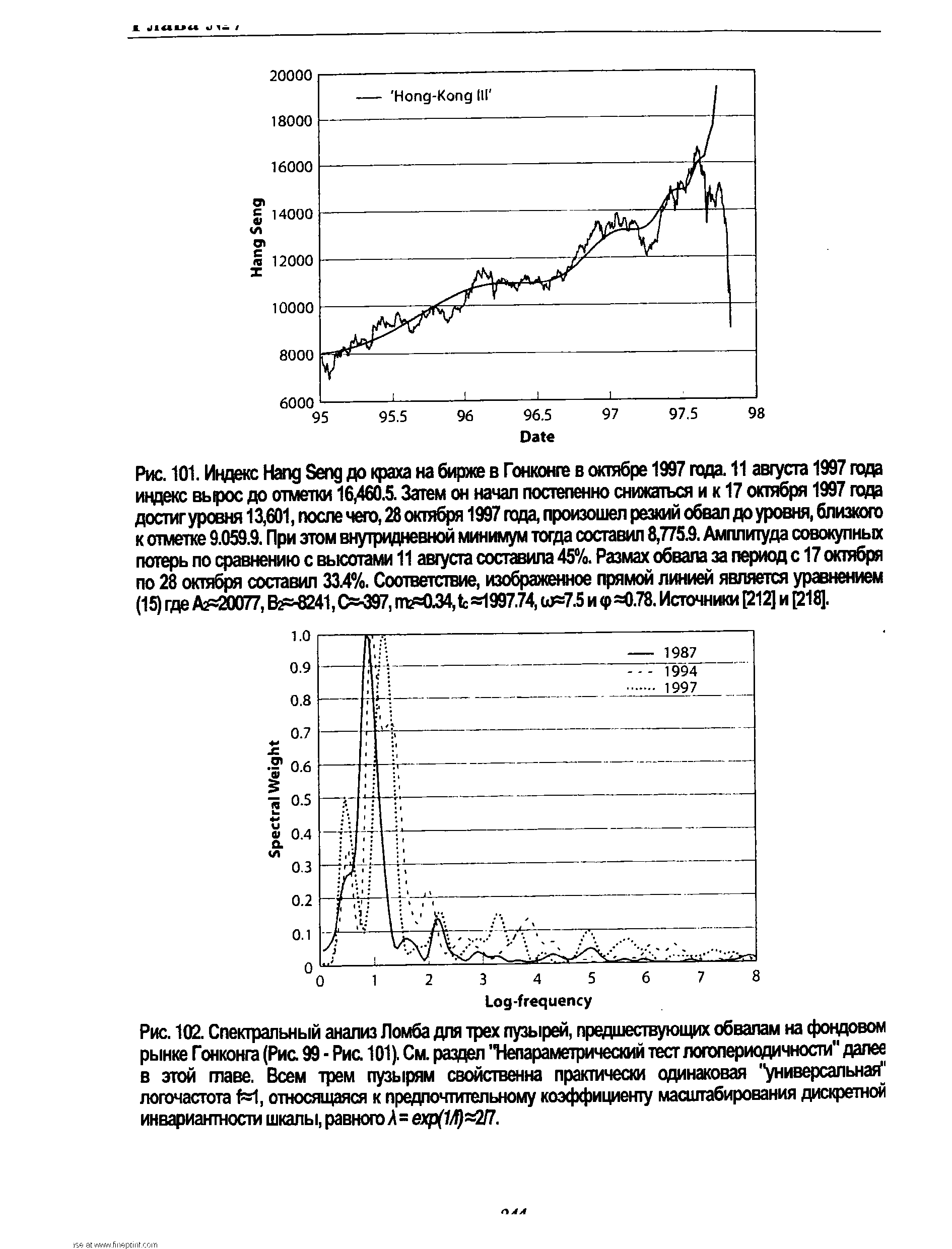
Как видно из Табл. 10, безразмерные параметры т2, (о, и Л, также как и предположительное время краха для соответствия всех четырех индексов очень хорошо согласуются за исключением экспоненты от , полученной по индексу ASPGEN. Фактически, значение, полученное для параметра предпочтительного коэффициента масштабирования, варьирует не более, чем на 5%, что говорит о том, что все четыре индекса демонстрируют высокую числовую стабильность. [c.300]
Эллиот и его последователи не нашли решения проблемы, составлять ли графики данных по линейной или полулогарифмической шкале. Полулогарифмическая шкала представляет определенный интерес, особенно при изучении недельных или месячных графиков с целью анализа цены и времени или при работе с коррекциями и расширениями. Мы считаем обсуждение проблемы линейного или полулогарифмического масштаба важным для профессиональных трейдеров. В данной книге все примеры приложения наших инструментов осуществлялись с использованием линейного масштабирования. Везде, где мы находим это необходимым — например, при описании расширений и коррекций на недельных данных, — мы кратко обсуждаем этот предмет. Однако мы не считаем этот вопрос стоящим усилий по интеграции дополнительной функции полулогарифмического масштабирования в наш пакет программ WINPHI. [c.35]
Чтобы судить о качестве работы ФИ-эллипсов для тех или иных продуктов, которыми предстоит торговать, необходимы тесты на долгосрочных исторических данных. Функция, наносящая исторические данные на графики с постоянной ценовой шкалой, уже интегрирована в программное обеспечение WINPHI. Дневные данные O-H-L -С за два или три года невозможно разместить в пределах ширины одного экрана, а при прокрутке экрана ценовой масштаб обычно изменяется, подстраиваясь под самый высокий максимум и самый низкий минимум наносимых данных. Функция WINPHI, позволяющая сохранять постоянную шкалу, ключевой элемент, потому что масштабирование по высоте экрана привело бы к искажению углов ФИ-эллипсов, прилагаемых к движениям рынка. [c.129]
При более последовательном подходе для улучшения процесса обучения можно использовать информацию о производных второго порядка от функции невязки. Соответствующие методы оптимизации называются квадратичными. Вся указанная информация собрана в матрице гессиана Н, имеющей размеры Nw х Nw, где Nw — число весов. Эта матрица содержит информацию о том, как изменяется градиент при малых смещениях по различным направлениям в пространстве весов. Прямое вычисление матрицы требует большого времени, поэтому разработаны методы, позволяющие избежать вычисления и хранения матрицы (спуск по сопряженному градиенту, масштабированный метод сопряженных градиентов (см. [197]), RBa kProp (см. [212]), квази-ньютоновский метод, метод Левенбер-га-Маркара). [c.32]
Наконец, для некоторых функций преобразования, реализованных в выходном узле, возникают проблемы с масштабированием. Сигмоид определен на отрезке [0,1], поэтому выходную переменную нужно масштабировать так, чтобы она принимала значения в этом интервале. Известно несколько способов масштабирования сдвиг на константу, пропорциональное изменение значений с новым минимумом и максимумом, центрирование путем вычитания среднего значения, приведение стандартного отклонения к единице, стандартизация (два последних действия вместе). Имеет смысл сделать так, чтобы значения всех входных и выходных величин в сети всегда лежали, например, в интервале [0,1] (или [-1,1]), — тогда можно будет [c.60]
Смотреть страницы где упоминается термин Масштабирование
: [c.321] [c.72] [c.493] [c.493] [c.493] [c.214] [c.152] [c.70] [c.200] [c.212] [c.213] [c.239] [c.257] [c.258] [c.258]Смотреть главы в:
Дизайн и реклама (2006) -- [ c.188 ]