Примеры физической модели — синька чертежа завода, его уменьшенная фактическая модель, уменьшенный в определенном масштабе чертеж проектировщика. Такая физическая модель упрощает визуальное восприятие и помогает установить, сможет ли конкретное оборудование физически разместиться в пределах отведенного для него места, а также разрешить сопряженные проблемы, например, размещение дверей, ускоряющее движение людей и материалов. Автомобильные и авиационные предприятия всегда изготавливают физические уменьшенные копии новых средств передвижения, чтобы проверить определенные характеристики типа аэродинамического сопротивления. Будучи точной копией, модель должна вести себя аналогично разрабатываемому новому автомобилю или самолету, но при этом стоит она много меньше настоящего. Подобным образом строительная компания всегда строит миниатюрную модель, прежде чем начать строительство производственного или административного корпуса или склада. [c.225]
При выполнении анализа технико-экономической эффективности НИР выбор методов и средств зависит не только от целей анализа, но и от объема исходной информации, которая есть на данной стадии НИР. Так, на стадии разработки технического задания имеется весьма ограниченный круг данных, поэтому, естественно, расчеты по узкому кругу укрупненных показателей носят ориентировочный характер. Широко используются методы экстраполяции, моделирования, аналогов и т. д. При оформлении результатов НИР, когда имеются уже основные характеристики исследуемого объекта, расчеты, обосновывающие целесообразность проведения ОКР и внедрения объекта в производство, должны быть сделаны значительно более точно с использованием информации, накопленной в процессе проведения НИР. На этой стадии могут широко применяться методы математического моделирования, учитывающие структуру объекта, его основные конструкторские характеристики, результаты исследования физических моделей и т. д. [c.88]
Открытие этих законов состоялось гораздо позднее. Они вошли в науку и легли в основу физических моделей. Это простейшие и наиболее фундаментальные принципы отбора природа не знает случаев, когда бы нарушались законы сохранения. [c.8]
На протяжении столетий физика с успехом использует математические модели — как для познания мира, так и для прогнозирования результатов воздействия на него. Модели, основанные, скажем, на принципах ньютоновской механики, уже три века надежно служат человечеству, давая необходимую расчетную базу в его практической деятельности. Более того, прогресс самой математики в значительной степени связан с исследованием разнообразных физических моделей. Такие направления современной математики как теория дифференциальных уравнений, теория групп, топология и функциональный анализ тесно связаны с проблемами, возникающими в классической или квантовой механике, термодинамике и т. д. Можно сказать, что сейчас человечество обладает глубоким пониманием методологии применения математики в естественных науках. [c.25]
Моделирование базы данных ведется поэтапно, при этом выделяется несколько уровней абстракции, каждому из которых соответствует свой вариант модели. Необходимость выделения нескольких уровней абстракции определяется сложностью процесса отображения предметной области в базе данных. Привязку логической модели к программным и техническим средствам называют физической моделью базы данных. Она и дает конечное материализованное воплощение процессов создания базы данных. [c.147]
Методы наглядного представления Графические модели Физические модели Должностные описания и инструкции [c.705]
Модель накопления данных формализует описание информационной базы, которая в компьютерном виде представляется базой данных. Процесс перехода от информационного (смыслового) уровня к физическому отличается трехуровневой системой моделей представления информационной базы концептуальной, логической и физической схем. Концептуальная схема информационной базы (КСБ) описывает информационное содержание предлагаемой области, т.е. какая и в каком объеме информация должна накапливаться при реализации информационной технологии. Логическая схема информационной базы (ЛСБ) должна формализованно описать ее структуру и взаимосвязь элементов информации. При этом могут быть использованы различные подходы реляционный, иерархический, сетевой. Выбор подхода определяет и систему управления базой данных, которая, в свою очередь, определяет физическую модель данных - физическую схему информационной базы (ФСБ), описывающую методы размещения данных и доступа к ним на машинных (физических) носителях информации. [c.56]
Если набор объектов имеет описание (концептуальная модель), указаны свойства и логические связи между объектами (логическая модель) и известно их местонахождение в памяти ЭВМ (физическая модель), то это позволяет извлекать объекты и применять их в соответствии с назначением многими пользователями. Следовательно, организуется объектная база данных. [c.157]
Таким образом, переход к физической модели базы данных, реализуемой и используемой на компьютере, производится с помощью системы программ, позволяющих создать в памяти ЭВМ (на магнитных и оптических дисках) базу хранимых данных и работать с этими данными, т.е. извлекать, изменять, [c.158]
Моделирование - одна из основных категорий теории познания на идее моделирования, по существу, базируется любой метод научного исследования как теоретический, при котором используются различного рода знаковые, абстрактные модели, так и экспериментальный, использующий предметные, физические модели. [c.85]
Физические модели — это некоторые реальные системы, в которых реализуются те или иные взаимодействия между элементами и частями изучаемого объекта. Они могут быть полными, частичными и аналоговыми. Полные модели представляют собой объект, измененный в масштабе с возможностью выполнять полностью или частично функции реального объекта. Так, например, при изучении эффективности очистки воды строится опытная очистная станция, ее конструкция представляется в реальном масштабе. Для изучения отдельных частей этой станции могут быть созданы частичные модели, например система обеззараживания воды. [c.8]
Модели подразделяют на физические, аналоговые и математические. Физические модели представляют увеличенные или уменьшенные копии объекта или системы, они редко применяются в экономическом анализе. Аналоговая модель представляет исследуемый объект аналогом, который ведет себя как реальный объект, но не выглядит как таковой. Известные каждому экономисту графики, иллюстрирующие соотношения между объемом производства и издержками, являются аналоговой моделью. График пока- [c.12]
В целом процесс построения полей риска проходит ряд последовательных стадий. Вначале определяются источники опасных воздействий. Ими могут быть промышленная установка, хранилище опасных веществ, трубопроводы под давлением, паровые котлы и т.д. Далее разрабатывается физическая модель, в соответствии с которой происходит распространение разрушающего или [c.98]
Метод определения центра тяжести физической модели системы распределения (используется для определения места расположения одного распределительного центра). Метод аналогичен определению центра тяжести физического тела. Суть его состоит в следующем. Из легкого листового материала вырезают пластину, контуры которой повторяют границы района обслуживания. На эту пластину в местах расположения потребителей материального потока укрепляют грузы, вес которых пропорционален величине потребляемого в данном пункте потока. Затем модель уравновешивают (рис. 101). Если распределительный центр разместить в точке района, которая соответствует точке центра тяжести изготовленной модели, то транспортные расходы по распределению материального потока на территории района будут минимальны. [c.337]
| Рис. 101. Определение места расположения склада методом построения физической модели материальных потоков | 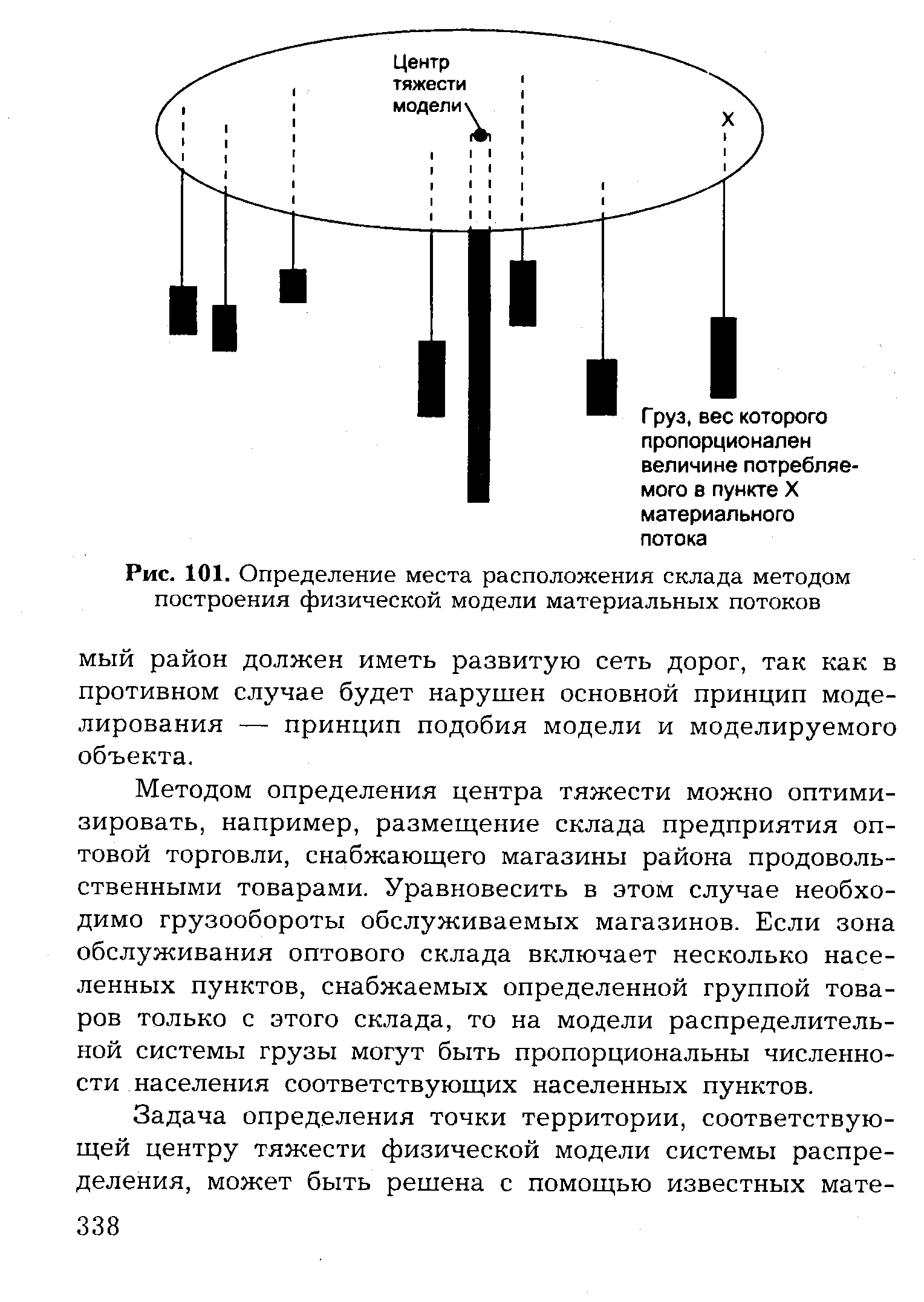 |
| Рис.. 102. Определение места расположения склада методом поиска центра тяжести физической модели системы распределения | 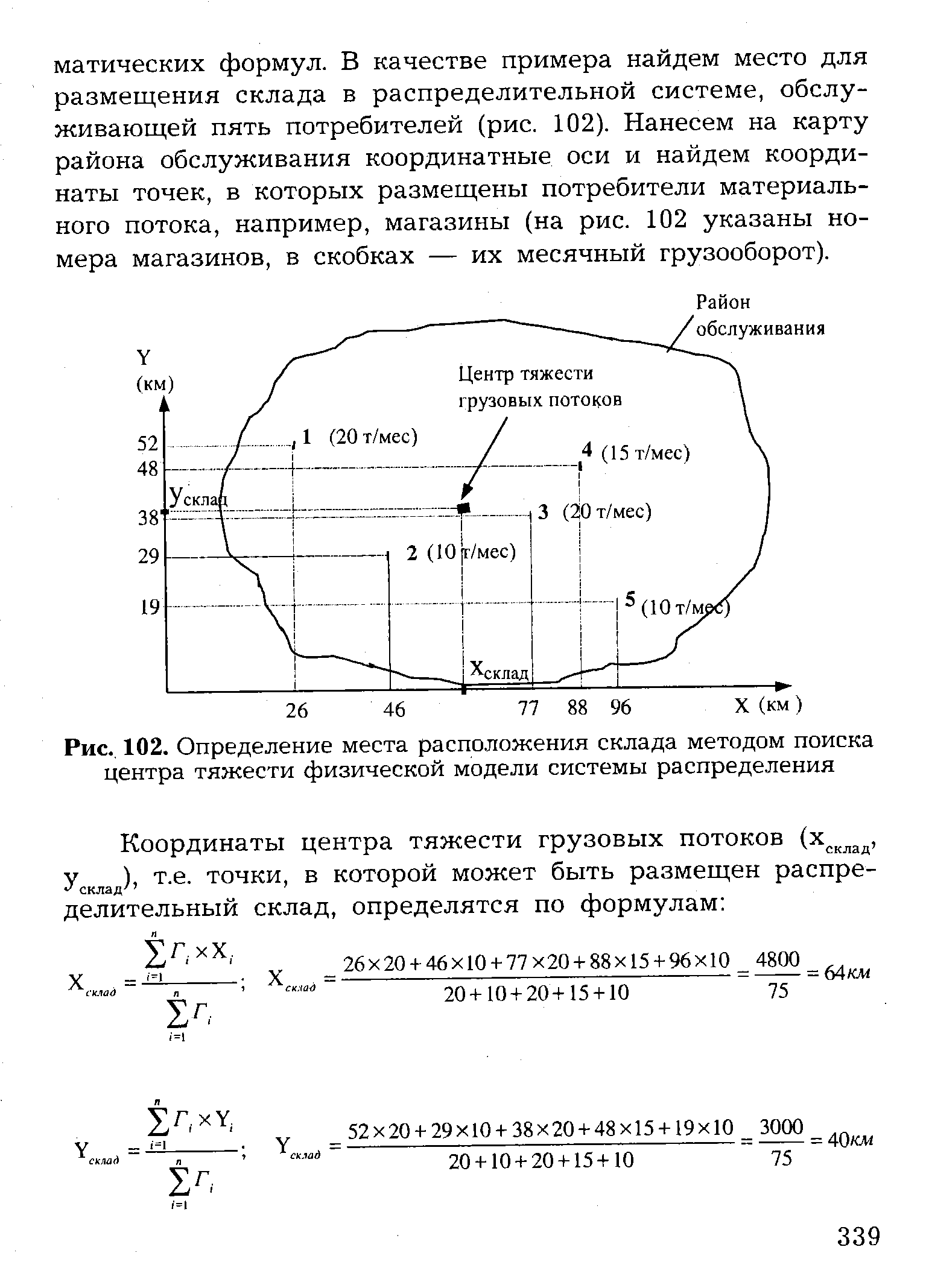 |
Наиболее просто пояснить предлагаемые подходы вероятностно-статистического метода нормирования при наличии корреляционной связи между нормообразующими факторами второй группы на примере расчета специфицированной нормы для марки материального ресурса в случае, когда требуется учесть небольшое количество этих факторов. При этом физическую модель изменения запасов проиллюстрируем для предприятия-потребителя с дискретным процессом снабжения (поставки не каждый день) и непрерывным процессом отпуска (ежедневный расход) нормируемой марки материального ресурса. Процессы снабжения и расхода в течение года будем рассматривать как неравномерные, изменяются (варьируют) значения следующих нормообразующих факторов объемов и интервалов поставок, объемов суточных отпусков. В данном случае корреляционная связь между нормообразующими факторами начинает учитываться при значении коэффициента корреляции, рассчитанного между объемами поступления в интервалах и суммарными объемами отпуска за этот же период и соответствующего величине JIQ/U > 0,60 (где JIQ/U — рассчитанный коэффициент корреляции). [c.361]
МОП может быть представлена как математическими соотношениями, так и графически в виде графов или эквивалентных схем. В [34] все методы построения моделей объекта проектирования разделены на две группы. Первая из них предназначена для построения моделей элементов и всего объекта и предполагает использование неформальных (эвристических) приемов для выбора вида математических соотношений. В этом случае возможны два подхода — теоретический и экспериментальный. Первый основан на использовании физических закономерностей, характеризующих процессы, связанные с объектом. При построении модели вводят ряд допущений с учетом особенностей объекта и требуемой точности отображения зависимостей. Математические соотношения чаще всего представляются системами уравнений. Экспериментальный подход связан с проведением испытаний на самих объектах или на их физических моделях. Сюда же можно отнести и вычислительный эксперимент на полных математических моделях. По экспериментальным данным методами аппроксимации, усреднения или статистической обработки строят макромодели объекта. [c.63]
Имитационное моделирование как один из методов анализа систем применяется в тех случаях, когда сложно или просто невозможно использовать другие виды анализа и нужно проследить за ходом протекающих процессов, а постановка эксперимента на физической модели по каким-либо причинам невозможна. Для имитационного моделирования необходимо определить изучаемую систему, установив ее границы, переменные и константы, показатели эффективности, подобрать подходящую модель, описать модель на языке, приемлемом для ЭВМ, спланировать эксперимент и провести его, убедившись по первым пробным результатам в адекватности отображения действительных процессов в имитационной модели, обработать результаты экспериментальных данных. [c.186]
При выражении проблемы требуется указание ее предмета, характеристик, целей к путей их достижения. В результате обосновывается технология решения проблемы. Применительно к техническим объектам такая технология экспериментально проверяется на натурных физических моделях. [c.215]
О программировании. В наши дни каждый знает, что программа для ЭВМ — это алгоритм, составленный на языке машины. Сама ЭВМ — это физическая модель алгоритма выполнения программ (заданных на языке машины). Программирование представляет собой разработку алгоритмов и перевод их с одних языков на другие 5 . Программирование связано и с некоторыми нематематическими проблемами (проблемами экономии расходуемых средств, экономии времени, обеспечения удобств для персонала, обслуживающего ЭВМ, и т. п.), которые обычно называют прагматическими. Хотя в настоящее время в подавляющем большинстве случаев процесс программирования в значительной своей части опирается на искусство программиста, это не мешает нам утверждать, что программирование представляет собой применение аппарата теории алгоритмов к решению задач из других областей. [c.5]
Как было отмечено ранее, конечной стадией в процессе моделирования информационной системы предприятия по поставкам продукции с целью удовлетворения требований к данным, предъявляемым системой управления, является создание физической схемы, которая описывает внутреннюю физическую модель. Она не только реализует базу данных, в которой определяются данные и их связи, существующие в организации, но и представляет возможность извлекать необходимую информацию в той форме, которая нужна для управления. [c.130]
Методы моделирования основаны на замене реального объекта исследования его математической моделью (количественным описанием явления) или его физической моделью. Метод содержит построение модели, вариацию влияющих факторов, учет ограничений, перенос выводов с модели на реальный объект. [c.422]
Любая частная или комплексная задача управления имеет сегодня ряд модельных вариантов ее решения. Модели позволяют упростить сложные хозяйственные процессы, выделить в них наиболее значимые компоненты и связи, экспериментально проработать управленческие ситуации и осуществить прогнозные расчеты в условиях высокой неопределенности и большой глубины упреждения. В современном менеджменте используются три базовых типа моделей физические, аналоговые и математические. Пример широко применяемых в практике физических моделей — пространственные планировки предприятий, их цехов и служб, используемые для расстановки оборудования, размещения материалов и рабочих мест сотрудников. Аналоговые модели иллюстрируют поведение или структуру моделируемого объекта (например, в виде графика, гистограммы или структурной схемы). Наибольшие возможности оптимизации управленческих решений предоставляют математические модели — модели теории игр, теории очередей, управления запасами, линейного программирования, имитационные и модели экономического анализа. [c.23]
Физические модели. Будучи материальным воплощением реальной системы, физическая модель может являться частью моделируемой системы или ее аналогом, отличающимся от моделируемой системы геометрическими и другими параметрами. [c.241]
Из физических моделей, используемых в организации и управлении строительным производством, наибольшее распространение получили следующие их разновидности [c.241]
К достоинствам физических моделей относятся наглядность, надежность результатов наблюдений, возможность своевременно внести коррективы. К недостаткам — сложность их организации и осуществления, потребность в одновременном использовании значительного числа исследователей, а также сравнительно высокие затраты на создание уникальных моделей. [c.242]
Существует много разновидностей моделей графики и таблицы, физические модели, логические и математические выражения, машинные модели, имитационные модели. [c.75]
Способ представления — материальные (физические, т.е. совпадающие предметно-математические) и символические (языковые). Материальные физические модели соответствуют оригиналу, но могут отличаться от него размерами, диапазоном изменения параметров и т.п. Символические модели абстрактны и основываются на описании их различными символами, в том числе в виде фиксации объекта на чертежах, рисунках, графиках, схемах, текстов, математических формул и др. При этом они могут быть по принципу построения — вероятностными (стохастическими) и детерминированными по приспособляемости — адаптивными и неадаптивными по изменению выходных переменных во времени — статическими и динамическими по зависимости параметров модели от переменных — зависимыми и независимыми. [c.115]
Развитие здания математических моделей физических явлений происходит в основном в трех направлениях. Если в исследовании встречается ситуация, когда не удается подобрать подходящую модель в здании существующих моделей, то естественно попытаться получить нужную модель логическим путем из уже существующих моделей. Обычно это удается сделать (в этом-то и состоит зрелость современной физики). Если же это сделать не удается (что может произойти при исследованиях в тех областях, где здание физических моделей еще не построено), то приходится опираться непосредственно на эксперимент, выводить некоторые экспериментальные обобщения и строить модель на их основе. Такой подход к построению моделей называется феноменологическим. При этом происходит расширение здания моделей, оно распространяется на новые области, однако возможно, что одновременно произойдет и расширение вглубь, т. е. старые фундаментальные принципы окажутся следствием некоторых более глубоких принципов. Так, при распространении законов механики на околосветовые скорости Эйнштейн сформулировал новые принципы, из которых можно получить принципы механики Ньютона строго логическим образом, путем асимптотического перехода для скоростей, малых по отношению к скорости света. Принципы Ньютона, ранее имевшие чисто экспериментальную основу, теперь превратились в следствие более общих положений. Обратим внимание читателя на то, что построение моделей, связанное с логической надстройкой уже существующего здания физических моделей, по своей методике принципиально отличается от расширения здания на новые области и тем более от углубления его фундамента. Более того, большинство физиков относит к собственно научным [c.27]
Пожалуй, не можем, хотя такое здание интенсивно строится во всех трех направлениях. И хотя здесь имеются определенные аналогии с физическими процессами (такие аналогии излагаются, например, в книге Б. С. Разумихина Физические модели и методы теории равновесия в программировании и экономике , Москва, Наука , 1975 г.), экономическое моделирование много сложнее. Дело осложняется в первую очередь тем, что экономика охватывает не только производственные процессы, но и производственные отношения. Моделирование производственных процессов не представляет принципиальных трудностей и не намного сложнее, чем моделирование физических процессов. Моделировать же производственные отношения невозможно, не учитывая поведения людей, их интересов и индивидуально принятых решений. [c.28]
В условиях отсутствия физических моделей, связывающих техноло- [c.5]
Проектирование ПО с помощью ASE-систем. Оно включает несколько этапов. Начальный этап — предварительное изучение проблемы. Результат представляется в виде исходной диаграммы потоков данных и согласуется с заказчиком. На следующем этапе выполняется детализация ограничений и функций программной системы, и полученная логическая модель вновь согласуется с заказчиком. Далее разрабатывается физическая модель, т.е. определяется модульная структура программы, выполняется мифологическое проектирование базы данных, детализируются граф-схемы программной системы и ее модулей, проектируется пользовательский интерфейс. [c.120]
Наиболее просто пояснить предлагаемые подходы вероятностно-статистического метода на примере расчета специфицированной нормы для марки материального ресурса (МР) в случае, когда требуется учесть небольшое количество нормообразующих факторов второй группы. При этом физическую модель изменения запасов проиллюстрируем для предприятия-потребителя с дискретным процессом снабжения (поставки не каждый день), большой частотой поставок и непрерывным (ежедневным) процессом отпуска нормируемой марки материала1. При этом процессы снабжения и расхода в течение года будем рассматривать как неравномерные — меняются (варьируют) значения следующих нормообразующих факторов объемов и интервалов поставок, объемов суточных отпусков. Эта модель наиболее близка к Классической и достаточно подробно рассмотрена в экономической литературе, посвященной нормированию производственных запасов. Правда, в этих работах рекомендуется применять другие алгоритмы для определения специфицированной нормы, чем излагаемые ниже, но они не полностью учитывают специфику формирования запаса при данных условиях (более подробно см. гл. 3). [c.304]
В физических моделях, подобных аттрактору Лоренца, существуют особые измеряемые переменные, которые определяют их состояние. Для многих нелинейных систем эти переменные включают такие понятия, как температура, давление или плотность. Такие факторы в сумме отражают реакцию изучаемой системы на другие, внешние силы. Температура, в конце-концов не появляется сама собой. Она является результатом воздействия других сил, продуцирующих тепло. Физические науки удачливы— они могут измерять воздействие внешних переменных. На рынках мы сталкиваемся с различными окружающими условиями. Рынки, в конечном счете, подвергаются влиянию плохо измеряемых сил. Так, три динамических переменных, подразумеваемых фрактальной размерностью 2.33 американского фондового рынка, не будут легко идентифицируемыми локальными факторами, такими, как например Р/Е (отношение цены акции к ее прибыли) или GNP (валовой национальный продукт). Вместо этого ведущие силы на рынках больше подходят под характеристику глобальных, выяснение которых может стать результатом совместных усилий фундаментальной и технической мысли. Мое собственное мнение состоит в том, что растяжение фазового пространства порождается рыночными эмоциями или техническими факторами. Образование складок, которое выносит цены обратно на аттрактор, порождается истинными ценностями, или фундамента ттьными факторами Таким образом, ожидание (или па-строение) определяет степень разогретости рынка, в то время как ценности определяют пределы аттрактора. Третьим фактором, который мог бы играть роль, аналогичную плотности жидкости, может выступить рыночная ликвидность. Ликвидность, в конце концов, и есть причина существования Рынка. [c.213]
Физическая модель метода LIFO -это склад с одним входом и выходом [c.309]
Физическая модель метода, FIFO — это склад с отдельным, входом и выходом [c.311]
Логико-информационные схемы Логические модели Моделирование Оргасхемы Оргачертежи Статистические модели Теоретико-множественные модели Топологии процессов Физические модели [c.277]
