Исходя из содержания счетов и требований потребителя к выходной информации общую матрицу счетов можно расчленить на частные матрицы (матрицы группы счетов), придерживаясь одного из двух принципов экономического содержания или корреспонденции счетов. [c.87]
При формировании матриц группы счетов по первому признаку на первый план выдвигается проблема корреспонденции между группами счетов, так как может возникнуть корреспонденция между счетами, находящимися в разных группах. Необходимо решить вопрос, в какой частной матрице их отражать. [c.88]
Для решения этой проблемы применяется прием, при котором межгрупповые корреспонденции счетов могут добавляться к частным матрицам по дебетуемым (или кредитуемым) счетам. Обороты между группами желательно сосредоточить в специальной части частной матрицы, т. е. прибавить их к итогу дебетовых (или кредитовых) оборотов в разрезе определенной группы счетов. [c.88]
Следовательно, вместо одной общей матрицы счетов с размерами 100-100 имеется 12 частных матриц, размеры которых по порядку 4-4, 15-15, 10-10 и т. д. Исходя из реально существующей корреспонденции в группе счетов в квадратных матрицах групп счетов могут встречаться нулевые строки и столбцы, которые желательно исключить. Тогда размеры частных матриц уменьшатся и примут вид прямоугольника. [c.88]
Включим эти корреспонденции в частные матрицы групп счетов по дебетуемому счету. Тогда первая межгрупповая корреспонденция (кредит 05 и дебет 03) прибавится к матрице первой группы счетов, а вторая — к третьей. [c.88]
Формирование частных матриц по второму признаку, т. е. исходя из корреспонденции счетов, представляет собой расчленение элементов общей матрицы счетов по информационному содержанию. В этом случае отпадает проблема межгрупповой корреспонденции, так как все элементы общей матрицы счетов всегда принадлежат к определенной группе. Каких и сколько частных матриц формируется из общей матрицы счетов Это зависит прежде всего от конкретных целей использования информации, содержащейся в частных матрицах. [c.88]
Из сказанного следует, что определение частных матриц по принципу корреспонденции счетов более всего отвечает требованиям метода рационального формирования выходной информации, которому отдается предпочтение при делении элементов общей матрицы счетов. Кроме того, этот метод позволяет одновременно учитывать расчленение общей матрицы счетов и по принципу экономического содержания счетов. [c.89]
Как видно из таблицы, частные матрицы (1), (2), (3) составляются на одни и те же дебетуемые счета, но в корреспонденции с разными кредитуемыми счетами. Производственные затраты, например, можно группировать по видам используемых ресурсов и т. д. В частную матрицу (4) входят все дебетовые обороты счетов 8. .. 22, а в частную матрицу (5) — все дебетовые обороты счетов 23. .. 40. Таким образом, облегчается рассмотрение оборотов по приходу определенных видов ресурсов. Из сказанного следует, что в приведенном примере за основу формирования частных матриц принята группировка информации дебетуемых счетов (формирование затрат, приход ресурсов и т. д). Это дополняется расчленениями в части кредитуемых счетов, отражающих виды израсходованных ресурсов, источники их образования и т. д. [c.89]
Б заключение отметим следующее. До проектирования матриц групп счетов необходимо составить макет общей матрицы счетов, указав в нем все фактически существующие корреспонденции счетов (проводки) и нулевые элементы (без корреспонденции). Формированию частных матриц должен предшествовать анализ матрицы счетов с точки зрения рационального потребления информации и удовлетворения потребителя. [c.91]
На основе частных матриц предпочтительности каждого эко [c.401]
После этого намечается несколько основных стратегий (способов использования средств и ресурсов) решения частных задач. Находят вероятность реализации каждой из стратегий по каждой цели Устанавливают экспертную оценку относительной важности достижения определенной цели. Расчет выполняется с помощью специальной матрицы. При этом по каждой стратегии (строка в матрице) рассчитывается математическое ожидание как сумма произведений веса цели на вероятность ее осуществления при реализации рассматриваемого направления. В качестве оптимального принимается направление, математическое ожидание которого имеет наибольшее значение по сравнению с другими возможными стратегиями решения задач. Нормирующими условиями задачи являются сумма удельных весов критериев и сумма относительной важности отдельных целей, равная единице. [c.250]
Анализ значений / ,б, RH, RM матрицы коэффициентов частных корреляций приводит к аналогичному. выводу, поскольку значения /-критерия не превышают табличного значения. [c.81]
Матрицы частных корреляций [c.82]
Однако прежде чем окончательно выбрать группу основных факторов, необходимо проанализировать по табл. 35—36 возможность существования линейной зависимости между выбранными факторами х, —х5. Анализ матриц коэффициентов парных и частных корреляций показывает, что среди их элементов нет коэффициентов корреляций, превышающих или равных пороговому (6 = 0,74-0,8), что свидетельствует об отсутствии линейной зависимости между факторами. [c.82]
В такой ситуации надо переходить к реализации алгоритма частного балансирования рассматриваемых матриц. [c.105]
В сфере монтажа алгоритм частного балансирования матриц принципиально не должен изменяться за исключением того, что матрицы монтажа должны быть в общем сбалансированы, а максимальный объем монтажных работ, т.е. [c.106]
Самая общая и типичная статистическая задача в экономическом анализе — изучение наличия, направления и интенсивности связей между показателями. Это первый этап познания закономерностей формирования результатов хозяйственной деятельности. Предположение о наличии и тесноте связи делается в случае выявления общих закономерностей в вариации значений изучаемых показателей. Источник возникновения этих общих закономерностей может быть разным — причинно-следственная связь между показателями, зависимость от общего фактора, случайное совпадение элементов вариации. Задача экономического анализа — раскрыть качественную основу взаимосвязи между количественными характеристиками экономических процессов. Стохастическое исследование связи происходит с помощью методов корреляционного анализа — коэффициентов и отношений корреляции. При этом в зависимости от характера исходной информации применяются разные приемы корреляционного анализа оценка парной корреляции между показателями с цифровой шкалой измерения ранговая корреляция и коэффициенты, рассчитанные по так называемым матрицам сопряженности для анализа связей между качественными показателями каноническая корреляция для анализа связи между группами показателей частная корреляция, которая позволяет исследовать связь между двумя [c.111]
Эти сведения вводятся в ПЭВМ и рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации, множественные коэффициенты корреляции и детерминации. [c.145]
Изучая матрицы парных и частных коэффициентов корреляции, можно сделать вывод о тесноте связи между изучаемыми явлениями. Коэффициенты парной корреляции характеризуют тесноту связи между двумя показателями в общем виде с учетом взаимосвязей факторов, оказывающих воздействие на результативный показатель. [c.145]
| Таблица 7.7 Матрица частных коэффициентов корреляции |  |
Построение матрицы цели - средства для характеристики частных показателей интенсификации [c.224]
Структура группирует по существенно важным признакам юридические и экономические отношения организации. Методология этой группировки носит статистический характер, и ее принципы позволяют сделать вывод о том, что бухгалтерский учет может рассматриваться как частный случай экономической статистики. При этом надо помнить, что модель структуры имеет форму прямоугольной матрицы, где по столбцам перечисляются дебетуемые счета, а по строкам — кредитуемые. [c.166]
Анализируя столбцы матрицы, можно сделать вывод, что первая группа (варианты 4 и 7) представляет неиспользуемую информацию, частично это избыточная, частично необходимая, но упускаемая из поля наблюдения информация вторая (варианты 2, 5, 8) — представляет собой частный случай третьей группы (варианты 3, 6, 9). Последняя группа создает условия для серийного кодирования хозяйственных операций по типам документов. [c.192]
Если экономика имеет развитый институт финансовых посредников, то ее можно подразделить на четыре основных сектора домохозяйства, коммерческие фирмы, государственный сектор и финансовые институты. Они формируют матрицу требований друг к другу, показанную на рис. 3.1, который представляет гипотетический баланс каждого сектора. Домохозяйства являются конечными владельцами всех коммерческих фирм от нефинансовых корпораций до частных финансовых институтов. Особая роль финансовых посредников обнаруживается при анализе их активов, имеющих, как правило, финансовую форму. Они владеют сравнительно небольшим количеством недвижимости. На правой стороне их баланса доминируют финансовые обязательства, т. е.. финансовые организации занимаются трансформацией прямых требований в косвенные, более привлекательные для инвесторов. [c.39]
Характеристическое уравнение 271 Целая положительная степень квадратной матрицы 260 Циклическая компонента 134 Частная корреляция 128, 129 [c.306]
Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому чтобы реализовать то или иное отображение, т.е. найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью рассматриваемой задачи и с описанными выше частными случаями разбивают на несколько этапов. [c.122]
Применяется также морфологический метод, сущность которого заключается в разложении рассматриваемой проблемы на структурные компоненты, или параметры. На первом этапе проблема описывается в целом и никакие решения не принимаются. На втором - проблема разбивается на частные компоненты, влияющие на общее решение проблемы. На третьем этапе для каждого компонента подбираются альтернативные решения. Они вводятся в специальную матрицу (морфологический ящик), и с ее помощью вычленяется наиболее оптимальное решение. [c.90]
Легко видеть, что во всех рассмотренных частных случаях решение, если корни системы допустимы, является решением задачи и при том единственным. Действительно, пусть существует другое решение, некоторый набор X, отличный от х. Покажем, что эти наборы не могут отличаться. Так, при i3=n оба эти набора должны обращать определитель расширенной матрицы (11) в нуль, и отличие их невозможно по сути выбранных частных случаев. При /<л они не могут отличаться вследствие единственности решения системы (п — 1)-го линейных уравнений с п — 1 неизвестным при отличном от нуля определителе системы. [c.158]
В нашем случае m = п. Решение при этом сводится к составлению матрицы А = Р.ю. и выбору из каждой ее строки и каждого столбца по одному элементу таким образом, чтобы сумма их оказалась наибольшей. Это один из частных случаев задачи линейного программирования. [c.93]
Да, Abi,.- ДЬ - частные определители которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы. [c.50]
В результате получим матрицы коэффициентов парной и частной корреляции (рис. 2.8). [c.72]
| Рис. 2.8. Матрицы коэффициентов парной и частной корреляции |  |
Расчленение общей матрицы счетов можно осуществить и при ее разделении на несколько матриц, содержащих группы счетов (частные матрицы). Ведь существуют группы синтетических счетов, например разделы плана счетов, тесно связанные между собой корреспон-денциями (табл. 4.4). Например, счета производствен- [c.85]
| Таблица 4.5 Расчленение общей матрицы счетов (40x40) на частные матрицы | 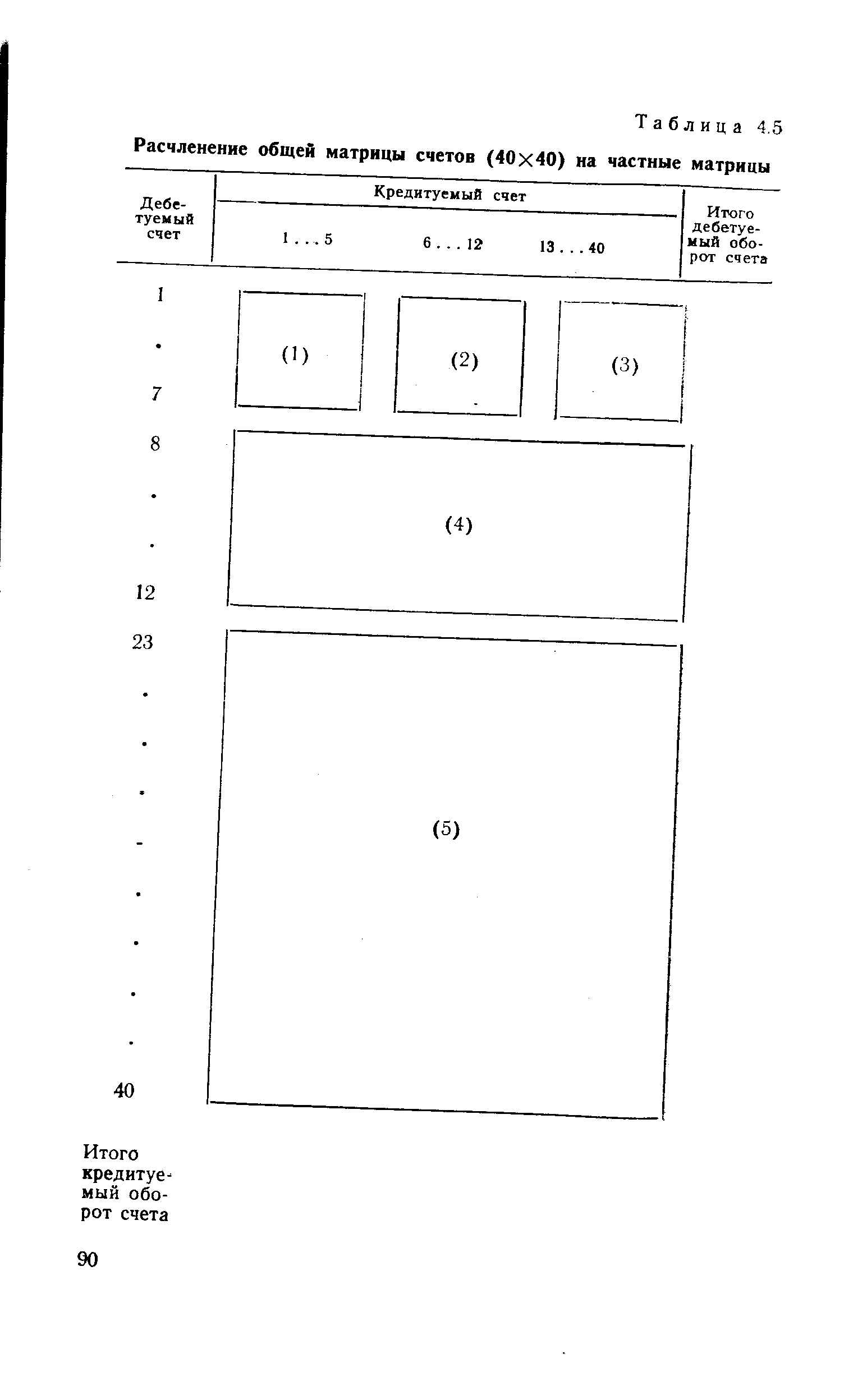 |
Однако анализ позиции СБЕ в матрице Рост/Доля рынка не позволяет четко определить стратегические цели компании. В то же время эта матрица — частный случай мультифакторной матрицы бизнес-портфеля, предложенной компанией General Ele tri (рис. 3.4, а). Рассмотрим гипотетическую компанию, в состав которой входят семь СБЕ, специализирующихся на производстве приборов и арматуры. В данном случае площадь каждой окружности соответствует размерам некоего рынка доля рынка СБЕ показана темным сектором. Так, компании принадлежит примерно 30 % рынка (среднего размера) зажимных устройств. [c.124]
Решение возникающей задачи может быть осуществлено при помощи алгоритмов решения СТЗ ДО (однако их применение требует дополнительного обеспечения специальными приемами связности графа задачи) и алгоритмов, учитывающих блочный характер матрицы СТЗ. В статье [12] рассмотрены соответствующие модификации алгоритма К. В. Кима и известного метода декомпозиции. Вычислительные аспекты рассмотренных сетевых задач обсуждаются в статье [16]. В частности, соответствующие графы могут иметь большую размерность вследствие многократного дублирования (по числу продуктов) вершин и дуг исходной транспортной сети, однако на практике существует возможность существенного уменьшения этой размерности. В статье даются сравнительные оценки этих моделей для случая, когда возможно применение их обеих. Результаты весьма огра--ниченного эксперимента показали некоторую предпочтительность более частной модели. [c.71]
При появлении в процессе расчета нескольких детале-операций с одинаковым частным значением Тц.. они запускаются на станки последующих операций и вводятся в расчет Тч х в порядке очередности их расположения в матрице. [c.167]
При пересчете числовой модели календарного плана на режим непрерывной работы станков в табл. 43 из табл. 37 переносятся данные операционной трудоемкости обработки деталей, а также все частные (подетальные) сроки календарной занятости первого станка и конечные сроки календарной занятости станков при обработке последней детали, т. е. календарные сроки по первому столбцу и последней строке матрицы. Далее по всем станкам, начиная со второго, по формуле (48) последовательно рассчитываются снизу вверх по столбцу матрицы новые частные сроки календарной занятости станков по выполнению закрепленных за ними детале-операции. Так, для второго станка получим 36 — 3 = 33 33 — 7 = 26 и 26—2 = 24. Вновь полученные сроки календарной занятости этого станка удовлетворяют условиям, выраженным [c.175]
К сожалению, в ППП MS Ex el нет специального инструмента для расчета линейных коэффициентов частной корреляции. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого 1)в главном меню последовательно выберите пункты Сервис / Анализ данных / Корреляция. Щелкните по кнопке ОК [c.71]
Смотреть страницы где упоминается термин Частные матрицы
: [c.85] [c.81] [c.276] [c.130] [c.73] [c.186] [c.83]Смотреть главы в:
Организация автоматизированной информационной системы бухгалтерского учета -> Частные матрицы
