ДОСТАТОЧНОЕ УСЛОВИЕ СТАЦИОНАРНОСТИ ТРАЕКТОРИИ 79 [c.79]
Принцип максимума — достаточное условие стационарности траектории [c.79]
Заметим, что выше сформулированы относительно слабые результаты ясно, что от метода трубки, так же как и от всех практически реализуемых методов, нельзя требовать нахождения глобального минимума метод заслуживает внимания и может быть использован, если для него стационарными траекториями (тупиковыми ситуациями) являются действительно стационарные, удовлетворяющие необходимому условию оптимальности — принципу максимума — траектории. [c.134]
Режим эндогенного роста может быть менее предпочтителен для индивидов, даже если он может быть реализован. Если выигрыш интегральной полезности от увеличения свободного времени перевешивает потери от более низкого роста потребления, то домохозяйства выбирают экзогенный рост. Мы не можем аналитически оценить благосостояние для равновесной траектории, поэтому используем приближенные оценки для стационарных траекторий. Каждая из них определена соотношением начальных значений факторов [c.18]
Уравнения (3.18)-(3.20) аналогичны уравнениям (2.10)-(2.12), определявшим стационарную траекторию роста для закрытой экономики. Уравнение (3.21) является условием равновесия на рынке капитала для стационарного роста. Оно получается из (3.12), (3.20) и условия распределения капитала уу = (г/а)"1//3 t/Д-. Заметим, что равновесие автаркии с zy = 1 для всех у является решением (3.21). [c.26]
Рассмотрим выбор между эндогенным и экзогенным стационарным ростом для стационарных траекторий. Темп роста одинаков для обоих режимов, и поэтому мы сравниваем только эффекты уровня. Из (2.24) экзогенный рост предпочтительней, если [c.41]
Наряду с этим плановые модели не могут быть столь же абстрактными, как это допустимо для моделей теоретико-методологического характера. Те факторы, от которых вправе абстрагироваться ученый исходя из целей своего исследования, зачастую обязательно должны быть учтены в плановой модели, пусть даже весьма приближенно. Это можно проиллюстрировать на примере того же межотраслевого баланса. Известно, что весьма содержательные выводы о характере траектории экономического развития получены из анализа межотраслевой модели с постоянными во времени технологическими коэффициентами (в частности, показано, что через определенный переходный период экономическая система, описываемая такой моделью, выходит на стационарный режим с максимальным темпом роста). В то же время в плановой практике межотраслевые модели с постоянными коэффициентами затрат неприменимы, так как это означает по существу отказ от учета в расчетах воздействия на эффективность общественного производства научно-технического прогресса. Поэтому в практических расчетах в межотраслевые модели вводится приближенное (пусть иногда весьма грубое) описание динамики коэффициентов материалоемкости, фондоемкости, трудоемкости единицы продукции, отражающее предполагаемые и планируемые сдвиги в технике и технологии общественного производства. [c.119]
Сами по себе стационарные точки дифференциального уравнения (4.13) особого интереса не представляют. Они важны тогда, когда к этим точкам сходятся траектории уравнения (4.13). Попытаемся проанализировать качественную картину поведения траекторий на основе характерной ситуации, изображенной на рис. 11. [c.76]
Траектория называется стационарной, если показатели не изменяются во времени [c.218]
Стационарная оптимальная траектория [c.346]
СТАЦИОНАРНАЯ ОПТИМАЛЬНАЯ ТРАЕКТОРИЯ — см. Магистраль. [c.346]
Стационарная оптимальная траектория 177, 346 [c.490]
Развитие познания на основе дифференциации парадигм проявляется в неравномерности уровня научного освоения разных сторон экономической жизни. Преимущество имеют простые картины экономической реальности экономические системы в состоянии равновесия или на траектории стационарного роста экономическое поведение стандартизированных, последова- [c.163]
Теорема. Если траектория управляемой системы [и ( ), х ( ) удовлетворяет принципу максимума, то она является стационарной. [c.79]
В остальном вариация 8и ( ) произвольна. Тогда bF0 [hi ( )] В этом состоит утверждение о стационарности подобной траектории. Доказательство. Из принципа максимума следует [c.80]
Оптимальная траектория удовлетворяет уравнению (2.30), но теперь она не обязательно стационарна и, следовательно, [c.38]
Этому начальному значению фондовооруженности соответствует оптимальное начальное значение потребления i(0) = = ун(5л) — точка А на рис. 2.1. В этой точке S<0, t <0 и оптимальная траектория, выходящая из точки, А, такова, что значения переменных у и S убывают. Пусть экономическая система, начав в момент времени t = О движение из точки А, попадает в момент времени t в некоторую точку Б(у, 5Б), причем 5Б > 5. Оптимальная траектория, выходящая из точки Б, не может зависеть от того, как и откуда (из точки А или из какой-то другой) экономическая система попала в точку Б. Оптимальное начальное значение для S(/,) = y (S ). Поэтому первая координата точки Б имеет значение у = уи(5Б), т.е. точка Б принадлежит кривой y (So). Это значит, что, поскольку точки Л и Б произвольны, все оптимальные траектории лежат на кривой t/K(S0). Экономическая система, начав движение из точки Д движется к стационарной точке (у, S ). Аналогичным образом, если движение начинаемся из точки В на рис. 2.1, то, поскольку в этой точке у < 0, 5 > 0, экономическая система будет двигаться к стационарной точке (у, S ). Наконец, если в начальный момент времени экономическая система находилась в стационарной точке (у, S ), то она так и останется в этой точке магистрального роста. Суммируя, можно записать [c.40]
| Рис.4.1 Переходы между состояниями марковской цепи эволюции макросреды Распределение переходных вероятностей на различных временных срезах характеризует уровень доверия эксперта к экономическим действиям существующего и будущих правительств. Оценки эксперта позволяют построить марковский прогноз развития экономической ситуации. Иллюстративный прогноз на 2001-2005 гг. в предположении, что в настоящее время Россия испытывает период стагнации, представлен в табл. 4.2. В последней графе приведено стационарное распределение марковской цепи, которое практически достигается уже через 6 лет. Из прогноза видно, что, если так пойдет и впредь, то вероятность кризисов и периодов быстрого роста достаточно велика и ее нельзя сбрасывать со счетов. Отметим, что даже в столь простом случае цепь содержит 55=3125 различных траекторий, то есть сценариев, каждый из которых имеет вероятность реализации, не превышающую 0,00032. | 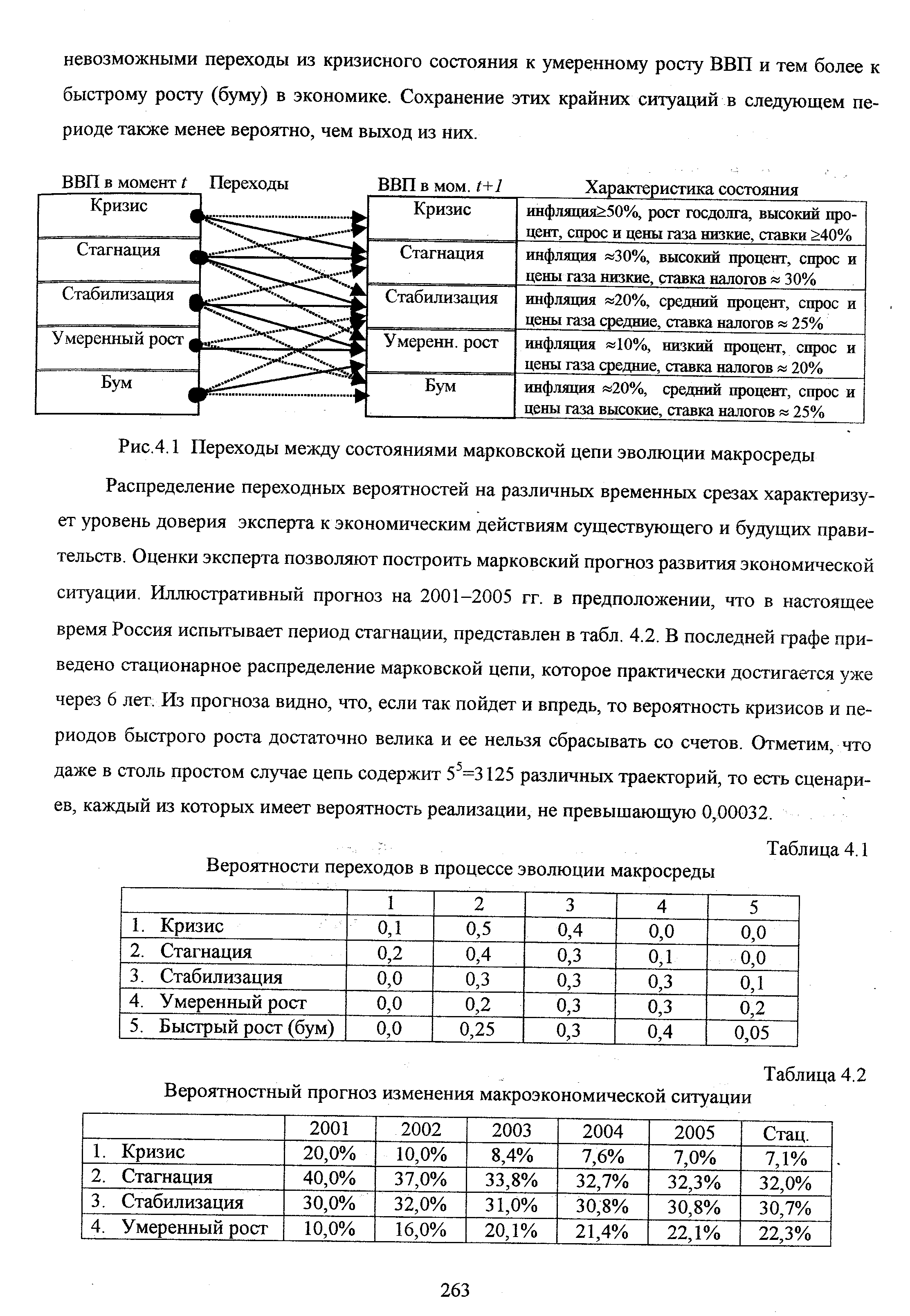 |
Модель также позволяет описать траекторию сходимости к стационарному состоянию. Пусть у — значение yt в стационарном состоянии. Тогда можно показать, что имеет место следующее приближенное соотношение [c.103]
Определим стационарное состояние, как состояние, в котором капитал на единицу эффективного труда постоянен kA = 0, тогда стационарный капитал k A определяется из условия sf(k A) = (n + 5 + g)k A. В стационарном состоянии капитал на одного эффективного рабочего kA постоянен, откуда следует, что УА=/( л) и сл=(1 8)Ул также постоянны. Это означает, что подушевой капитал k, равный AkA, а также с и у в стационарном состоянии растут с постоянным темпом, равным темпу технического прогресса g. При этом запас капитала и уровень выпуска (К и У) в стационарном состоянии растут с темпом (n+g). Заметим, что, как и ранее, другие экзогенный параметры (норма сбережения, норма амортизации, производственная функция) влияют лишь на траекторию перехода к стационарному состоянию и стационарный капитал, но не влияют на темпы роста в стационарном состоянии. [c.262]
Из поля направлений видно, что устойчивая седловая траектория (проходящая через точку А) проходит по фазовой плоскости как показано на рисунке слева направо, сверху вниз (иначе было бы противоречие с полем направлений). Обозначим седловую траекторию, входящую в т. А слева за В, а траекторию, входящую в стационарную точку справа — за С. Исходящие траектории обозначим за С и D (соответственно сверху и снизу). [c.135]
Q < с А- При этом возможны 2 варианта седловая траектория С проходит через с0 при s > О или не проходит. Если проходит, то фирма выбирает s так, чтобы оказаться на данной седловой траектории, после этого с будет уменьшаться (запас сотрудников "проедаться" для получения сиюминутной прибыли), a s будет постепенно увеличиваться. Фирма будет подходить к стационарному состоянию. [c.135]
Провал траектории ряда в 1942 - 1944 г.г. не позволяет трактовать этот ряд как стационарный на всем периоде с 1940 по 1965 годы. Поэтому мы продолжаем далее рассматривать значения ряда только на послевоенном периоде - с 1946 по 1965 г.г. [c.46]
Мы не рассматриваем стационарные состояния с нулевыми х или г, так как им не соответствуют траектории сбалансированного роста. [c.14]
Траектория сбалансированного роста в данном режиме является стационарным состоянием системы (2.19)-(2.20), (хМ, Их>), которое находится непосредственно [c.18]
Недостаток модели эндогенного роста с человеческим капиталом (и свободным временем) заключается в том, что она генерирует слишком высокие темпы сходимости к стационарной траектории. Чтобы этого избежать, Ortiguera, Santos (1997) ввели в модель издержки новых инвестиций и получили темпы сходимости близкие к эмпирическим оценкам. Мы могли бы последовать их примеру, однако не делаем этого, поскольку преследуем иные цели. Поэтому в дальнейшем используется описанная выше версия модели, допускающая простое обобщение на глобальный уровень. [c.21]
Это требование сильнее стандартного запрета на игру Понци, относящегося к бюджетному ограничению (3.2) и выполненного для стационарной траектории с отрицательным zy <е. [c.27]
МАГИСТРАЛЬ [turnpike] — основное понятие математической теории равномерного пропорционального роста экономики, основы которой были заложены американским математикомДж. фон Нейманом. Это траектория (путь) развития, при которой теоретически за длительное время достигается максимальная скорость роста экономики (другие названия —неймановская траектория, траектория максимального сбалансированного роста, стационарная оптимальная траектория). Предпосылками существования такой траектории в рамках неймановской теории являются довольно жесткие требования модели расширяющейся экономики пропорции использования технологических способов неизменны, экономика растет с постоянным [c.177]
УСТОЙЧИВОСТЬ СИСТЕМЫ [stability of a system] — способность динамической системы сохранять движение по намеченной траектории (поддерживать намеченный режим функционирования) несмотря на воздействующие на нее возмущения. Основными видами У.с. явля-ются равновесие, гомеостазис, стационарный режим (циклическое повторение одной и той же последовательности состояний). [c.373]
Условие K/L = onst обеспечивает для модели (33) — (37) стационар у — k — I. Так как ЕК - - EL = 1, а дУ/дК, К/У и L/Y — величины постоянные на траектории стационарного роста, то и dY/dL = onst, причем [c.60]
Но уравнение для х1 в силу Аг—0 очень просто, и из условий х1 (Т)=0 и и1 (t) 0 следует, что первое слагаемое (144) будет найдено точно, какой бы ни была функция и1 (t) (а в данной задаче имеется семейство решений, дающих одно и то же минимальное значение F0, так что и1 (t) определяется с большой степенью неопределенности). Таким образом, вся ошибка численного решения связана с ошибкой во втором слагаемом, и относительная погрешность в нем составляет 12,5% для метода локальных вариаций и 0,3% в наших расчетах. В [41 ], [86] исходная траектория характеризуется как точка локального минимума вариационной задачи. Это, как показали наши расчеты, неверно. Легко проверить (предоставим это читателю), что исходная траектория является стационарной точкой метода локальных вариаций принятая в этом методе техника варьирования траектории действительно не приводит к изменению значения функционала. Но это есть следствие дефекта метода, а не особенность данной траектории. Ведь если бы мы имели дело с локальным минимумом задачи, то и наш метод не позволил бы эту траекторию проварьировать как и всякий реализуемый метод, он является методом поиска лишь локального минимума. Поэтому замену функционала (2) на функционал [c.280]
Предпринимательская функция. В главе 1 Шумпетер описывает потетическое стационарное состояние кругооборота , которое хар теризуется неизменным набором, количеством, атакже способами у требления всех производимых благ. В этих условиях полной инфор ции о настоящем и будущем продукт без остатка распределяется MI ду владельцами производительных благ, так что не возникает не тс ко остаточный доход, но и процент (здесь Шумпетер расходится с Б Баверком — см, гл, 11). Основные идеи теории экономического раз тия Шумпетера изложены в главе 2. Для того чтобы экономика oi со своей привычной траектории и резко изменила свои собствен показатели , должны быть осуществленытак называемые новые к< бинации , основными видами которых являются I) производство вых благ 2) применение новых способов производства и коммер- кого использования благ существующих 3) освоение новых рын [c.306]
Во-вторых, простейшие модели экономич. роста, использованные в проекте Месаровича—Пестеля, теоретически хорошо изучены, известны их устойчивые стационарные режимы, т. е. те состояния, к к-рым стремятся траектории таких моделей. В частности, известно, что увеличение нормы накопления вызывает лишь краткосрочное увеличение темпа прироста выпуска именно в тот момент, когда норма накопления возрастает. В дальнейшем, когда она стабилизируется на пек-ром новом (пусть даже достаточно высоком) уровне, начинается процесс постепенного снижения темпов развития, к-рые вновь приближаются к стационарным. Поскольку поддержание высокой нормы накопления в развивающихся регионах за счёт внутренних ресурсов неосуществимо из-за ограничений на потребление, использование указанных моделей даже при осмысленных производств, функциях автоматически приводит к выводу о неизбежности увеличения иностр. помощи тем же темпом, каким растёт экономика развивающегося региона. Однако из-за того, что использованные Месарови-чсм и Пестелем модели не могут уловить влияния структурных сдвигов в нар. х-ве регионов и переводят весь анализ в плоскость темпов роста, возникает противоречие между необходимостью более быстрого роста развивающихся регионов и ограниченными возможностями развитых стран, не способных наращивать свою помощь в необходимых для этого масштабах. [c.617]
Замечание 2. Исходя из смысла условий 1)-5), можно переформулировать определение процесса Леви так это стохастически непрерывный процесс со стационарными независимыми приращениями, выходящий из нуля и имеющий траектории, непрерывные справа с левосторонними пределами. [c.245]
Пуанкаре построил другую модификацию принципа стационарного действия, в которой действие определено на траекториях в фазовом пространстве - пространстве обобщенных координат ql. .. q" и импульсов р . . . . . . р . Действие есть функционал вида [c.23]
Утверждение о стационарности функционалов (2.18) и (2. 19) на истинной траектории называют принципом Гамильтона (или соответственно принципом Гамильтона— Остроградского и принципом Гамильтона в форме Пуанкаре). [c.23]
Рассмотрим гармонический осциллятор — материальную точку на пружинке, положение точки задается функцией x(t), кинетическая энергия равна 1Лтх2, а энергия пружины - ViAjr2. Согласно принципу Гамильтона -Остроградского истинная траектория есть стационарная точка функционала [c.184]
В соответствии с принципом Гамильтона - Остроградского истинные траектории являются стационарными точками функционала (6.1) на множестве функций (6.2), (6.3). [c.213]
Если же седловая траектория С не проходит через с0 при s > О (она успела уйти в область минусовых s), то s становится равной нулю, и с естественным образом уменьшается до тех пор, пока не достигнет такого значения, чтобы фирма могла перейти на седловую траекторию. При этом s = 0, а с уменьшается. Начиная с момента перехода на седловую траекторию s постепенно увеличивается (по мере подхода к стационарной точке А от 0 до s(A), а с уменьшается до с А). Таким образом, в данном случае фирма будет постепенно уменьшать количество работающих за счет "недостаточного" (т.е. меньшего, чем в стационарной точке) приема на работу, при этом скорость приема на работу будет увеличиватсья, а количество работающих — уменьшаться. В определенных случаях может возникнуть ситуация, когда фирма никого не будет принимать на работу. [c.136]
Мы изучаем переходную равновесную динамику чуть ниже, а сейчас рассмотрим траекторию эндогенного сбалансированного роста. Выпуск, потребление и оба вида капитала растут на этой траектории экспоненциально с одинаковым постоянным темпом, а распределение времени домохозяйств неизменно. Уравнения для данной траектории соответствуют стационарному состоянию5 сис- [c.14]
Множественность стационарных решений обусловлена положительной взаимосвязью между процентной ставкой и темпом эндогенного роста, проявляющейся в уравнениях (2.11) и (2.13). Стационарные ставки процента г и г2 существенно отличаются для эмпирически оправданных значений параметров модели. Ladron-de-Guevara et al (1999) подчеркивают качественные отличия между траекториями стационарного роста, отвечающими данным корням. Однако минимальный корень (2.16) во многих случаях является неправдоподобным решением. Время на производство знаний должно быть положительно, что для стационарного состояния влечет [c.15]
