Значения средних рангов Xj могут выражаться (что чаще и бывает) целыми числами с остатком. Они преобразуются в целочисленную шкалу рангов. Показателю с наименьшим значением среднего ранга приписывается ранг 1 и т.д. Если исходить из гипотезы о линейной зависимости значимости показателя Bj от его ранга Г , то [c.62]
Ускоренная амортизация по методу уменьшаемого остатка. В соответствии с данным методом нормы линейной амортизации дополняются поправочными коэффициентами по специальной шкале в зависимости от срока службы оборудования (табл. 14.1). [c.208]
В этом случае установление конкретной формы связи между процентной ставкой и коэффициентами риска проводится с некоторыми допущениями, основными из которых являются ряд процентной ставки имеет столько же значений, сколько и шкала коэффициентов риска каждому интервалу шкалы коэффициентов риска соответствует фиксированное значение процентной ставки применяется гипотеза о линейной зависимости между процентной ставкой и коэффициентами риска, т. е. [c.202]
А (- = >в систему (R =>, где А - множество классов эквивалентности системы (А >. Шкала т A->R называется шкалой порядка, если она единственна с точностью до монотонно возрастающих непрерывных отображений множества т (A) в R. Шкала называется шкалой интервалов, отношений или разностей, если она единственна с точностью до положительных линейных преобразований, растяжений или сдвигов, соответственно. [c.189]
Геометрически адекватной формой их отражения являются линейные координатные диаграммы. Геометрическими знаками-символами на таких диаграммах служат точки и последовательно соединяющие их прямые линии, складывающиеся в ломаные кривые, конфигурация которых дает представление об изображаемом процессе. Ось абсцисс является в такой диаграмме осью времени с равномерно размещенными отметками, а ось ординат — осью значений, которые принимает с течением времени изучаемый показатель. По отметкам обеих шкал определяют местоположение точек в координатном поле диаграммы, а последовательно их соединяя, находят кривую динамики изображаемо- [c.71]
Крестики-нолики. Для построения данного вида графиков используются те же данные, что и для построения линейного графика (т. е. цены открытия, закрытия или другие цены одних и тех же параметров). Для этого графика не существует шкалы абсцисс. Это отличает крестики-нолики от всех других типов графиков. Идея построения графика заключается в отметке крестиком (при росте цены) или ноликом (при ее падении) каждого колебания в обусловленном ранее масштабе (например, 5 базисных пунктов). С точки зрения реального времени график ненагляден, т. к. фиксирует чистое ценовое движение. [c.68]
Прежде, чем применять наши разработки к уровням восстановления правилам входа, стоп-лоссам и целевым прибылям на графиках, обсудим "за" и "против" линейной и полулогарифмической шкалы. [c.56]
Сравнение линейной полулогарифмической шкал [c.57]
Эллиот и его последователи и не смогли договориться, должны ли исследования фигур графиков проводиться с использованием линейной и/или полулогарифмической шкалы. [c.57]
Шкалы на приведенном линейном графике показывают равные расстояния между всеми ценами от 700.00 до 1,500.00 на полулогарифмической шкале приращения уменьшаются по мере увеличения значений ценовой шкалы. Иными словами, на графике расстояние от 700.00 до 800.00 намного больше, чем расстояние от 1,400.00 до 1,500.00. Это означает при работе с ценой и временем и измерении расстояния мы получаем на линейной и полулогарифмической шкалах разные результаты. [c.57]
Пример показывает, что длина импульсной волны от впадины №5 до пика №6 равна 3,9 см на линейной шкале и 3,4 см на полулогарифмической. Соответствующие коррекции 38,2% равны 1,5 см на линейной шкале и 1,3 см на полулогарифмической. [c.57]
На линейной шкале корректирующее движение от пика № 6 к впадине № 7 равно 1,5 см, что делает его коррекцией, соответствующей уровню восстановления 38,2%. На полулогарифмической шкале, однако, корректирующий ход составляет только 1,1 см. Это означает, что уровень восстановления оказывается пропущен из-за узкого, но решающего разрыва в 0,2 см. [c.58]
На линейных шкалах выбор отправной точки временного ряда не влияет на результат, потому что расстояние от одной до другой точки графика остается постоянным. С другой стороны, даже с учетом искажений, Эллиот сам указывал, что работа с полулогарифмическими шкалами может быть полезна, когда применяется в дополнение к линейному масштабу. [c.58]
Касательно каналов тренда Эллиот отмечал "Обычно, когда используется арифметическая (линейная) шкала, волна 5 заканчивается приблизительно на параллельной линии. Однако если волна 5 значительно превышает параллельную линию и композиция волны 5 указывает, что это ее фигура не закончена, тогда все движение с начала волны I должно быть построено на полулогарифмической шкале. Конец волны 5 может достигать, но не превышать параллельную линию" (Эллиот, с. 60). [c.87]
В Уроке 12 упоминалось, что когда волна 3 удлиняется, волны 1 и 5 стремятся к равенству или к соотношению 0.618, как показано на рис.4-3. Действительно, все три движущие волны стремятся соотноситься согласно математике Фибоначчи - или быть равными, или в пропорциях 1.618 и 2.618 (чьи инверсии равны 0.618 и 0.382). Такие соотношения импульсных волн обычно выполняются в процентных величинах. Например, волна I с 1932 по 1937 г.г. набрала 371.6%, в то время как волна III с 1942 по 1966 г.г. набрала 971.7% или в 2.618 раза больше. Чтобы обнаружить эти соотношения требуется полулогарифмическая шкала. Конечно, на мелких волновых уровнях, линейный и полулогарифмический масштабы дают по существу один и тот же результат, так что количество пунктов в каждой импульсной волне показывают ту же кратность. [c.83]
При линейной зависимости, выражаемой приведенной формулой, угловой коэффициент равен тангенсу угла наклона нормативной линии к оси абсцисс, который при равенстве масштабов шкал определяется по формуле [c.211]
Шкала отношений — это единственная с точностью до линейных преобразований шкала вида [c.28]
Шкала разностей существенна с точностью до линейного преобразования вида [c.28]
Выделение разных уровней измерения дает известное основание говорить о внутреннем единстве задач классификации и измерения. В самом деле, неупорядоченная классификация есть не что иное, как построение шкалы некоторого признака (фактора), градациями которого являются названия классов. Таким образом, процедура построения неупорядоченной классификации может рассматриваться как процедура измерения по номинальной шкале. В случаях, когда полученные классы могут быть упорядочены по некоторому основанию, например по расстоянию или по мере сходства между собой так, чтобы стоящие рядом в этом ряду классы были более сходны друг с другом, чем отдаленные, говорят о линейно-упорядоченной классификации. В таких случаях построение классификации подобно измерению по порядковой шкале. [c.29]
По объективным причинам для социально-экономических измерений характерна низкая контролируемость их точности. Для проверки адекватности можно использовать ряд простых критериев. Например, оценка, представляющая собой линейную комбинацию величин разной размерности с безразмерными коэффициентами, заведомо не может быть адекватной, если не оговорено заранее совместное преобразование единиц измерения. Неадекватными будут оценки, построенные на основе арифметических операций с рангами (такие операции неприменимы к порядковой шкале). [c.31]
Шкалой интервалов называется шкала, в которой результаты измерений определяются с точностью до (инвариантны относительно) линейного положительного преобразования ф,(у,) = a,j> + с,-, где а, > 0 и с, — фиксированные числа. Типичным примером такой шкалы может служить шкала температур. Как известно, для измерения температуры имеются, например, шкалы Цельсия, Фаренгейта и Кельвина. Переход от результатов измерений в одной шкале к результатам в другой происходит по формулам вида у = а, у, + с,. [c.71]
Все перечисленные выше шкалы — абсолютную, отношений, разностей и интервалов относят к количественным шкалам. Понятно, что результаты измерения, инвариантные относительно линейного положительного преобразования у = а, у + с,, будут инвариантны и относительно преобразований вида yt = a yt и yi — yi + с,-. По этой причине среди количественных шкал наиболее общей оказывается шкала интервалов. Поэтому все утверждения, полученные для измерений, выполненных в шкале интервалов, будут иметь место и для измерений в шкалах отношений и разностей (тем более, для абсолютной шкалы). [c.71]
Поскольку рассматриваемый в книге количественный подход предполагает измерение значений критериев в количественных шкалах, то несомненный практический интерес представляет установление инвариантности включений (2.15) относительно линейного положительного преобразования критериев. Заметим, что если бы такой инвариантности на самом деле не было, то это означало бы невозможность применение предлагаемого подхода при решении практических многокритериальных задач с количественными критериями. [c.73]
Следствие 3.3. Включения (3.4) и (3.12) инвариантны относительно линейного положительного преобразования критериев /ь f2,. .-,/ ,, а значит, результаты теоремы 3.4 могут быть использованы для задач многокритериального выбора, в которых значения указанных критериев вычисляются в количественных шкалах (интервалов, отношений и разностей). [c.91]
Заметим, что упомянутые выше виды тестовых шкал (шкала стенов и Т-шкала) являются результатом стандартизации (линейного преобразования масштаба шкалы) в вид, удобный для практического использования. [c.402]
Под календарной диаграммой в ряде форм представления информации о графике реализации проекта понимается правая часть, на которой отформатированными отрезками в масштабе времени на календарной шкале показаны моменты начала и окончания задач, а также длительность их выполнения. Календарная диаграмма является частью линейной диаграммы (диаграммы Ганта), а также форм использования задач, графика ресурсов и использования ресурсов. Приведенные ниже алгоритмы показаны на примере линейной диаграммы, но в других формах представления информации [c.63]
К основным шкалам количественных признаков относятся шкалы интервалов, отношений, разностей, а также абсолютная шкала. По шкале интервалов измеряют величину потенциальной энергии или координату точки на прямой. В этих случаях на шкале нельзя отметить ни естественное начало отсчета ни естественную единицу измерения. Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования, т. е. линейные функции. Температурные шкалы Цельсия и Фаренгейта связаны именно такой зависимостью °С = 5/9 (°F — 32), где °С — температура по шкале Цельсия, a "F — температура по шкале Фаренгейта. [c.318]
Из количественных шкал наиболее распространенными в науке и практике являются шкалы отношений. В них есть естественное начало отсчета — нуль, т. е. отсутствие величины, но нет естественной единицы измерения. По шкале отношений измерены большинство физических единиц масса тела, длина, заряд, а также цены в экономике. Допустимыми преобразованиями в шкале отношений являются подобные (изменяющие только масштаб), другими словами, линейные возрастающие преобразования без свободного члена. , [c.318]
На Рис. 12 представлены дневные цены закрытия DJIA со 2 января 198( года до 31 декабря 1987 года. Это период времени соответствует увеличении интервала, заключенного между двумя почти вертикальными линиями на Рис. 11 Хотя Рис. 12 показывает лишь 8 из 210 лет ценовой динамики, представленной нг Рис. 11, оба рисунка необычайно похожи. Однако, необходимо сделать некоторые замечания, поскольку временные шкалы, используемые на этих рисунка различны (логарифмическая шкала по оси ординат на Рис. 11 и линейная шкаш Рис. 12). Мы выполним в главах №7 и №10 детальное сравнение информации наглядно представляемой графиками на этих двух рисунках. [c.42]
Эллиот и его последователи не нашли решения проблемы, составлять ли графики данных по линейной или полулогарифмической шкале. Полулогарифмическая шкала представляет определенный интерес, особенно при изучении недельных или месячных графиков с целью анализа цены и времени или при работе с коррекциями и расширениями. Мы считаем обсуждение проблемы линейного или полулогарифмического масштаба важным для профессиональных трейдеров. В данной книге все примеры приложения наших инструментов осуществлялись с использованием линейного масштабирования. Везде, где мы находим это необходимым — например, при описании расширений и коррекций на недельных данных, — мы кратко обсуждаем этот предмет. Однако мы не считаем этот вопрос стоящим усилий по интеграции дополнительной функции полулогарифмического масштабирования в наш пакет программ WINPHI. [c.35]
Поскольку многие читатели не знакомы с этой проблемой, представляем два типичных недельных графика Индекса S P500, чтобы продемонстрировать различие между линейной и полулогарифмической шкалами (рисунок 3.9). [c.57]
На рисунке 3.9 один и тот же набор недельных данных Индекса S P500 с июня 1996 года по декабрь 2000 года графически отражен дважды с использованием линейной шкалы на верхнем графике и полулогарифмической на нижнем графике. [c.57]
Проблема при работе с правильными каналами тренда в том, что никогда нельзя быть уверенным в том, как будет развиваться в будущем ценовая фигура. В большинстве случаев для отслеживания ценовых моделей, развивающихся в каналах тренда, линейное вьиисление надежнее, чем полулогарифмическое. Именно поэтому в программном обеспечении WINPHI мы сосредоточиваемся исключительно на линейных расчетах. Профессиональных аналитиков просят учитывать также графики на полулогарифмических шкалах. [c.87]
| Рисунок 4.5 Канал тренда в восходящем тренде, (а) линейная шкала (Ь) полулогарифмическая шкала. Источник FAM Resear h, 2000. | 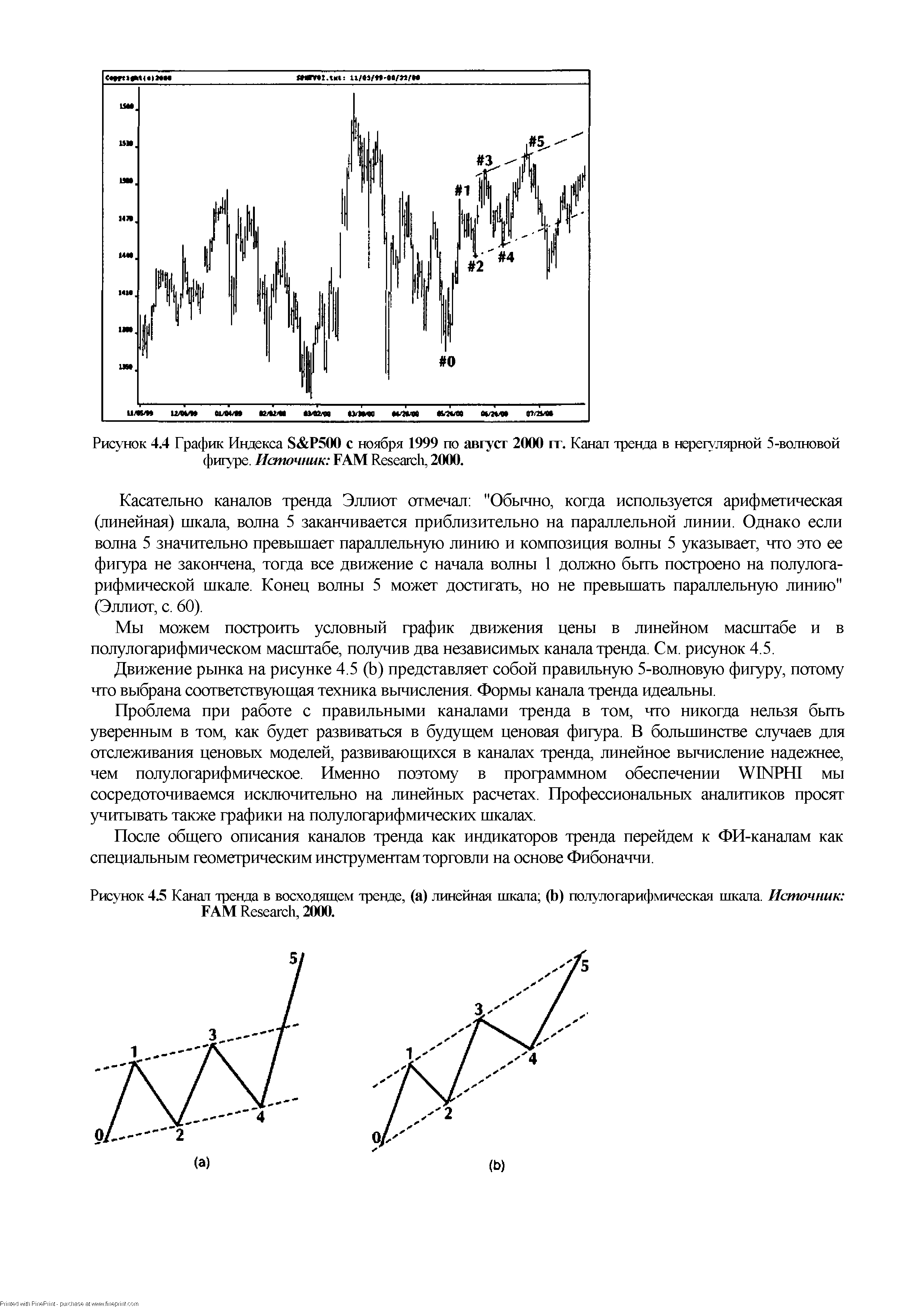 |
Для линейной шкалы /(у, f) = у t - С W(y t/V). Дифференци- [c.138]
Из доказательства последней теоремы видно, что коэффициент относительной важности 0, не является инвариантным относительно линейного положительного преобразования критериев. Более того, можно легко проверить, что он не является инвариантным и относительно преобразований вида ук = akykv. ук— ук + + ск, к = i,j. Это свидетельствует о том, что для различных измеряющих (различных ЛПР) коэффициенты относительной важности критериев будут различными, даже если они решают одну и ту же задачу выбора, имеют одинаковые предпочтения и выполняют измерения в шкале одного и того же типа. И в этом нет никакого Противоречия, поскольку указанные ЛПР могут использовать различные единицы измерения для одних и тех же критериев. [c.75]
Одним из наглядных способов планирования проектов служат линейные модели, в частности, график или диаграмма Ганта (Gantt hart). В графике Ганта сроки начала и окончания работ откладываются по горизонтальной шкале времени. Поэтому данная диаграмма является по существу графическим отображением календарного плана выполнения работ. Соответственно, размеры линий графика, отражающих отдельные работы, пропорциональны их продолжительности. Недостатками этого графика является следующее [c.4]
На рис. 2.2 приведена экранная форма, соответствующая линейной диаграмме. Для нее характерно разделение окна по вертикали на две части — слева расположена таблица, а справа календарная диаграмма. Каждая из этих частей окна имеет собственную полосу горизонтальной прокрутки (т. е. календарной шкалы) в нижней части экрана. Если поместить указатель мыши на стык этих полос прокрутки или на фаницу между частями окна (форма указателя при этом изменится), нажать и не отпускать левую кнопку мыши, то ее передвижением по горизонтали можно легко изменить распределение окна между таблицей и календарной диафаммой. [c.46]
Исследуются разнообразные математические формы Ф.п. одномерные и многомерные, аддитивные (общая полезность набора благ равна сумме полез-ностей отдельных благ), порядковые и количественные, мультипликативные, монотонные и немонотонные, линейные и нелинейные, одночленные и полиномиальные. Распространенным способом выражения Ф.п. являются шкалы. [c.380]
