А (- = >в систему (R =>, где А - множество классов эквивалентности системы (А >. Шкала т A->R называется шкалой порядка, если она единственна с точностью до монотонно возрастающих непрерывных отображений множества т (A) в R. Шкала называется шкалой интервалов, отношений или разностей, если она единственна с точностью до положительных линейных преобразований, растяжений или сдвигов, соответственно. [c.189]
| Рисунок 13. Пример одномерной карты двумерных данных. Стрелкой показана область нарушения непрерывности отображения близкие на плоскости точки отображаются на противоположные концы карты | 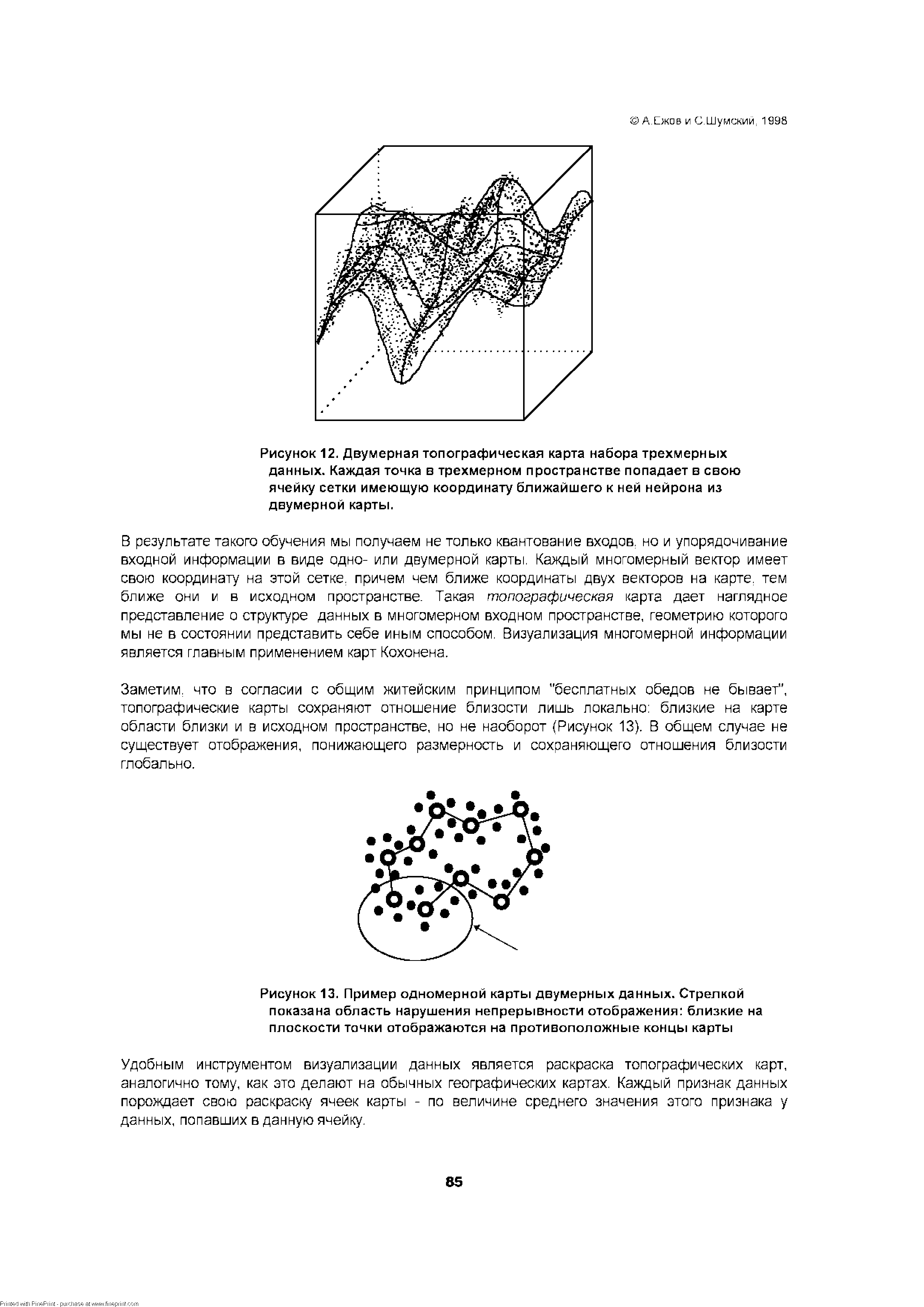 |
Заметим, что отображение j должно быть непрерывным по [c.287]
А.5. Q А —> A 9 m - однозначное непрерывное отображение, где [c.45]
В качестве критерия оптимальности в большинстве отраслевых задач выступает минимум затрат на заданный объем конечного продукта рассматриваемой производственной системы. Применяются экономико-математические модели разных типов динамические и статические, детерминированные и вероятностные, однопродуктовые и многопродуктовые, с дискретными и непрерывными переменными, производственные функции, производственно-транспортные задачи и, наконец, по характеру отображения хозяйственных связей —матричные и сетевые модели. [c.253]
Рассмотрим возможный вид вектор-функций F2 ( ) или F(-) в уравнениях динамической модели состояния (1.17), (1.18), основываясь на концепции структурно-алгоритмического механизма функционирования ИС. В соответствии с данной концепцией алгоритм функционирования и структуры ИС определяется характером её взаимодействия с интеллектуальной средой, обозначаемой через S и представляющей собой некоторое непрерывное множество (пространство, многообразие), на элементах которого осуществляется анализ характера выполнения цели С, стоящей перед системой I, и формирование на основании этого решения, направленного на выполнение данной цели С. Для этого из пространства Н на среду S с помощью некоторого оператора Р осуществляется отображение (проектирование) системы I, цели С и модели окружающей среды 0, воздействующей на объект (1.1) посредством векторов возмущения ш (в рассматриваемом случае информация о 0 сводится к соотношению (1.4)). Об операторе Р будем использовать предположение, что в области его значений, т.е. на множестве 1тР с S, существует обратный оператор Р 1. [c.26]
Геологическая обоснованность подсчетов запасов определяется тем, насколько правильной является принятая геологическая модель месторождения, т.е. представляемое отображение формы тел, характера и непрерывности залегания полезного ископаемого в пространстве недр. [c.80]
Лемма 4.3. Функционал Q (h)h определен на Vr, непрерывен (по h) и отображение X-+Q (K) равномерно непрерывно на V. Кроме того, для Y ЯеУ и /геЯ и таких, что K+ h Vr, справедливо соотношение [c.222]
Результаты, полученные в [9], позволяют при некоторых предположениях построить схему стохастической аппроксимации для решения более общей задачи — для вычисления безусловного минимума функции R(f(x)). Здесь f(x)= fi(x) , i = l,. .., г, по-прежнему вектор-функция векторного аргумента х, осуществляющая непрерывно-дифференцируемое отображение Rr на себя R(f) — скалярная функция. В задаче требуется вычислить вектор х, на котором достигается минимум R(f(x)) по наблюдениям систем случайных величин y(x)=f(x) + [c.375]
Т4. Если проект возможен, то тождественное отображение из познавательного пространства (S, Т°) в функциональное (5, Т1) — непрерывно. [c.27]
Система управления КАМО, использующая рельсовые линии связи, обеспечивает комплексную автоматизацию маневровой работы. Она может обслуживать любое количество маневровых локомотивов, обеспечивая автоматический контроль за их перемещением и функционированием тяговых и тормозных средств локомотивов при работе на станциях с любым числом стрелок и разным путевым развитием. Система управления КАМО обеспечивает непрерывный обмен информацией между локомотивами и постовыми устройствами автоматики с отображением точного места расположения локомотивов. Благодаря этому технически просто решаются задачи слежения за перемещением локомотивов, дистанционного управления стрелочными переводами из кабины машиниста и системного анализа маневровых команд, поступающих с локомотивов на центральный пост диспетчера. [c.42]
Суточный план-график — это графическое отображение процессов перемещения поездов и вагонов и выполнение с ними операций на подъездном пути. Он необходим для обеспечения бесперебойности процесса производства, ритмичности работы, непрерывности выполнения операций, наилучшего использования маневровых и технических средств, нормирования оборота вагонов на подъездном пути с расчленением по элементам и других показателей. Суточный план-график позволяет выявлять загрузку всех элементов подъездного пути, определить потребность в маневровых и технических средствах, организовать наилучшие условия взаимодействия в работе основных элементов подъездного пути между собой и со станцией примыкания, обеспечить наименьшие задержки поездов и ва-104 [c.104]
Замкнутость этого множества устанавливается аналогично, так как автоморфизм, очевидно (или, если угодно, в силу формулы (7.9)), является непрерывным отображением множества ситуаций на себя. П [c.175]
Прежде чем говорить о способах отображения цен на графиках, необходимо несколько слов сказать об основных характеристиках рыночной цены за определенный промежуток времени. В следующей части книги мы узнаем, что в течение одной торговой сессии цена акции изменяется в зависимости от плавающего предложения ценных бумаг. Эти колебания котировок, безусловно, интересны для внутридневных спекулянтов Однако для анализа тенденций они малопригодны. Инвесторам, равно как и краткосрочным игрокам, вполне достаточно знать результат торговли за определенный интервал или период времени. При этом самым важным временным интервалом является дневной, который вбирает в себя всю информацию о торговле за одну сессию. Дневные графики помимо всего правильно отображают присущий биржевым котировкам кусочно-непрерывный характер изменения цены [c.146]
Рассмотрим в пространстве R+ х П минимальную ст-алгебру , относительно которой измеримы все отображения (t, u>) <- Y(t, u>), порожденные -измеримыми при каждом t 0 (измеримыми) функциями Y = (Y(t,w))f2Q U d, имеющими непрерывные слева траектории (по t при каждом ш ft). [c.360]
Определение метрических пространств. Примеры. Пространство непрерывных функций. Полные метрические пространства. Принцип сжимающих отображений. Нормированные пространства. [c.16]
Вообще говоря, избыточный спрос является точечно-множественным отображением, но в ситуации, когда предпочтения строго выпуклы. Выше мы установили условия, когда совокупный спрос потребителя является непрерывной функцией. Если, в дополнение к этим условиям, технологическое множество каждого производителя является строго выпуклым, как предложение, так и совокупный избыточный спрос также являются непрерывными функциями. В этом случае мы можем для доказательства существования равновесия использовать аналоги утверждений предыдущего пункта. Так, в случае, когда технологические множества представляются производственными функциями, последние должны быть строго вогнутыми. Наиболее простой и часто рассматриваемый в экономической теории [c.175]
Рассмотрим задачу (Р) с постоянным отображением р(ж) = р. Предположим, что существует пара (ж, у), такая что у е г(х) и у е mt(P). Предположим, кроме того, что функция /(ж, у) дважды непрерывно дифференцируема и строго вогнута по у в некоторой окрестности точки (ж, у), и Vy /(ж, у) 0. Тогда решение задачи (Р) существует и единственно при любых ж из некоторой окрестности точки ж, причем функция г(х) непрерывно дифференцируема в этой окрестности. [c.547]
Заметим, что поскольку постоянное отображение непрерывно, непрерывность (полуне-препрерывность сверху) функции (отображения) предложения гарантируется при существовании решения задачи потребителя (поскольку функция прибыли непрерывна как функция цен). [c.699]
Учетно-плановая информация является отображением процесса социалистического расширенного производства, т. е. слож- ной динамической системы, непрерывно переходящей из одного состояния в другое. Наряду с этим ее нужно рассматривать как часть общей системы информации, абстрагируясь от общего к конкретному. Только в процессе исследования конкретного [c.49]
Напомним, что методом. дающим оптимальное представление информации в виде координат двумерной сетки, является построение топографических карт (карт Кохонена), о которых шла речь в Главе 4. Напомним в двух словах суть этой методики. В многомерное пространство данных погружается двумерная сетка. Эта сетка изменяет свою форму таким образом, чтобы по возможности точнее аппроксимировать облако данных. Каждой точке данных ставится в соответствие ближайший к ней узел сетки. Таким образом каждая точка данных получает некоторую координату на сетке. Такое отображение локально непрерывно близким точкам на карте соответствуют близкие точки в исходном пространстве (обратное, вообще говоря, не верно близким точкам в исходном пространстве могут соответствовать далекие точки на карте -такова цена понижения размерности). Таким образом, распределение данных на двумерной карте позволяет судить о локальной структуре многомерных данных. [c.192]
Для некоторых конфигураций количество весов явно превосходило число входных данных (наблюдений). Хотя недостаток степеней свободы делает оценку сомнительной, мы приводим здесь результаты работы 13-27-1 модели, чтобы проиллюстрировать доказанную Колмогоровым в 1957 г. и популяризованную Хехт-Нильсеном [137] теорему о существовании отображения. Эта теорема утверждает, что любая непрерывная функция может быть реализована трехслойной нейронной сетью, имеющей во входном слое т (в нашем случае 13) элементов, промасштабированных на [0,1], (2т-1-1) элементов-процессоров в единственном скрытом слое и п элементов в выходном слое. Таким образом, гарантируется, что иерархическая многослойная нейронная сеть может решить любую нелинейно отделимую задачу и может точно реализовать любое отображение га-мерных входных векторов в и-мерные выходные. При этом теорема ничего не говорит нам ни о возможности реализовать отображение посредством сети меньших размеров, ни о том, что для этого подойдут обычно используемые сигмоидные преобразования. [c.100]
Пусть дано измеримое/ пространство (Q, 2) и конечный набор мер р,ь. . ., ц,ге, определенных на этом пространстве. Сопоставим каждому множеству Ле2 вектор т(Л) = ц1(Л), цгИ),. . ., ц,п(Л) . Отображение m= ([Xi,. . ., цп), которое сопоставляет S некоторое множество от(2), называется векторной мерой, а множество wi(E) — множеством значений векторной меры /и. Векторная мера m называется конечной и непрерывной, если асе ц — конечные меры и для любого одноточечного множества А [c.21]
Теорема 4.9. Если отображение K- Q (K) равномерно непрерывно на V и Q строго выпукла на V, то метод покоординатного спуска, примененный к Q на V, сходится к точке минимума Q на V. [c.227]
Введенные функции и(х), Ф(х, у , v(x) и w(x) удовлетворяют всем условиям теоремы 3.5 3 настоящей главы, где wn = w. Действит тельно, в силу положительной определенности матрицы А, взаимной однозначности и непрерывности отображения f(x) имеем и(х)>0 при и inf и (к) >0 для любого s>0. Далее, [c.375]
Непрерывное увеличение объемов промышленного производства приводит к постоянному росту численности рабочих. Задачей статистики является правильное отображение движеция рабочей силы. Сопоставление за два и более месяца (или вообще за какие-либо периоды) списочной или среднесписочной численности рабочих дает лишь самое общее представление о динамике рабочей силы. Оно не раскрывает движения рабочих внутри периода. [c.97]
Таким образом, мы имеем дело с непрерывным отображением компакта симметричных ситуаций в себя. По теореме Брауэра это отображение имеет неподвижную точку, которая, как это было выяснено в ходе теоремы Нэша, является ситуацией равновесия. П [c.176]
Рисунки 7.1. и 7.2 представляют графики индекса курсов акций NASDAQ с апреля 1995 г. по декабрь 1996 г. в форматах, использующих отображение цены при помощи баров и линии. Обратите внимание, что график с отображением цены в виде непрерывной линии позволяет еще проще выделять тренды. На баровом графике корректирующей фигурой с августа 1995 г. по январь 1996г. является треугольник. На графике с отображением цены в виде линии этой фигурой является прямоугольник. Чтобы можно было провести сравнение, на графике с отображением цены в виде линии проведена нижняя линия фигуры, сформировавшейся на баровом графике. Разница очевидна. [c.68]
При планировании развития и размещения производства применяются экономико-математические задачи разных типов. Это зависит от специфики оптимизируемой отрасли, условий информационного обеспечения, а также накопленного исследовательскими и проектными учреждениями опыта. В частности, применяются задачи динамические н статические, детерминированное и вероятностные, однопродук-j тоаые и многопродуктовые, задачи с I дискретными и непрерывными пере- мецными, производственные и производственно - транспортные и, нако-I ней,, — по характеру отображения хо- зяйствеиных связен — матричные и сетевые. [c.100]
Способы доказательства существования равновесия основаны на демонстрации того факта, что некоторое, подходящим образом построенное, отображение имеет неподвижную точку, соответствующую состоянию равновесия, что, в свою очередь, опирается на варианты теоремы Брауэра о существовании неподвижной точки непрерывного отображения некоторого компактного множества (обычно, множества цен) в себя, или на ее непосредственное обобщение — теорему Какутани о неподвижной точке точечно-множественного выпуклозначного отображения компактного множества в себя. [c.165]
Пусть отображение Р(ж) компактнозначно и непрерывно, а /(ж, у) — непрерывная функция. Тогда [c.547]
Докажем, что отображение отклика, Дг(-), каждого игрока полунепрерывно сверху и его значение при каждом х г е Х г непусто и выпукло. Непустота следует из теоремы Вейер-штрасса (непрерывная функция на компакте достигает максимума). [c.645]
Если функция Р(р) непрерывна и положительна при р = р,, то выпуклозначное отображение д (р) полунепрерывно сверху в окрестности точки / . [c.698]
