Наряду со средними показателями эластичности в целом по совокупности регионов на основе частных уравнений регрессии могут быть определены частные коэффициенты эластичности для каждого региона. Частные уравнения регрессии в нашем случае составят [c.111]
Частные уравнения регрессии по отдельным видам вспашки составили [c.146]
Частные уравнения регрессии для отдельных типов домов, свидетельствуя о наиболее высоких ценах квартир в панельных домах, будут иметь следующий вид [c.147]
Число степеней свободы 49 Частные уравнения регрессии 109 [c.340]
Частные уравнения регрессии и частные коэффициенты эластичности. [c.15]
Частным уравнением регрессии модели y=a0+ai Xi +а2 х2 +,..., +ат хт + Е [c.16]
На основе линейного уравнения множественной регрессии постройте частные уравнения регрессии, рассчитайте частные коэффициенты эластичности и охарактеризуйте изолированное влияние каждого из факторов на результирующую переменную (в случае, когда другие факторы закреплены на среднем уровне). [c.11]
Частный коэффициент эластичности показывает, на сколько процентов в среднем изменяется производительность труда при изменении данного фактора на 1%. Для полученного уравнения регрессии коэффициенты эластичности соответственно равны Э2=+4,25 Э3=+0,38 34 = —5,69 Э5=+0,43. [c.201]
Оценка полученного уравнения регрессии по известным критериям показала, что данная модель удовлетворяет условиям адекватности (R — 0,95, t = 62,2, 6 = 8,8%). Частные коэффициенты эластичности и 3-коэффициенты, представленные в табл. 14, показывают, что наибольшее влияние на уровень затрат этой подсистемы оказывает коэффициент падения добычи нефти. Однако значение этого фактора в основном обусловлено природно-геологическими условиями разработки нефтяных месторождений, поэтому возможность его регулирования посредством воздействия извне ограниченна. [c.37]
Прогнозы по регрессионным моделям более надежны, поскольку они позволяют проводить эксперименты на моделях, в которых учитывается большее число факторов, влияющих на развитие процесса. Кроме того, полученные результаты всегда легко объяснить и обосновать. В силу этих причин прогнозы по уравнениям регрессии (иначе их называют производственными функциями) используются практически при экономическом прогнозировании всех видов макро- и микро-, краткосрочном и долгосрочном, частном и общем и т.д. [c.225]
Силу связи между вариациями себестоимости добычи нефти и газа п факторов определяют чистые (частные) коэффициенты корреляции. Они более соответствуют данной цели, чем парные коэффициенты корреляции, которые не свободны от корреляции с зависимой переменной прочих факторов, содержащихся в уравнении регрессии. Ввиду этого целесообразно остановиться на чистых коэффициентах корреляции. Наиболее сильно коррелируют с себестоимостью добычи нефти и газа (пятая строка, табл. 27) фондоемкость ( — 0,55), средний дебит ( — 0,49), время ( — 0,65), а наиболее слабо — удельная численность промышленно-производственного персонала (0,1). [c.92]
Следует усвоить, что коэффициенты частной детерминации - это доли от разных величин, поэтому они несравнимы по этим долям нельзя судить о роли факторов. Их главное практическое значение -определить, имеет ли смысл добавить в уравнение регрессии новый фактор или нет. Если при его включении ранее необъясненная вариация уменьшится на три четверти, как в примере при введении фактора х3, его включение оправдано если же коэффициент частной детерминации мал, то дополнительный фактор включать не следует. Сумма частных коэффициентов детерминации смысла не имеет и растет с ростом числа факторов и ростом R2 без ограничения. [c.282]
Для увязки этих частных индексов следует ввести корректирующий индекс, отражающий изменение свободного члена уравнения регрессии v по М [c.419]
Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией первого признака, входящего в множественное уравнение регрессии. [c.122]
Мера статистической значимости независимой переменной b уравнения регрессии Y = а + Ьх по влиянию на зависимую переменную Y. Рассчитывается как частное оценка коэффициента регрессии/стандартное отклонение. [c.471]
На первый взгляд может показаться, что матрица парных коэффициентов корреляции играет главную роль в отборе факторов. Вместе с тем вследствие взаимодействия факторов парные коэффициенты корреляции не могут в полной мере решать вопрос о целесообразности включения в модель того или иного фактора. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора с результатом. Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. При отборе факторов рекомендуется пользоваться следующим правилом число включаемых факторов обычно в 6—7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной вариации очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, a F- критерий меньше табличного значения. [c.100]
Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии. [c.121]
Данный коэффициент частной корреляции позволяет измерить тесноту связи между у и хг при неизменном уровне всех других факторов, включенных в уравнение регрессии. [c.124]
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так, по уравнению [c.125]
Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от —1 до +1, а по формулам через множественные коэффициенты детерминации — от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции, подтверждая ранжировку факторов по их воздействию на результат, на основе стандартизованных коэффициентов регрессии /3-коэффициентов) в отличие от последних дают конкретную меру тесноты связи каждого фактора с результатом в чистом виде. Если из стандартизованного уравнения регрессии Л = Дч q + V 2 + з г з следует, что , > 2 > /3XJ, т. е. по силе влияния на результат порядок факторов таков Х , х2, х3, то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции, ГуХ] хт > г 2, Х ХЗ > г хт. [c.127]
В табл. 3.2 приведены три значения / -критерия. В первой строке показан общий / -критерий. Он составил 19,3 и характеризует значимость двухфакторного уравнения регрессии в целом. Вторая величина F— 22,0 характеризует значимость парной регрессии у = а + Ь Х при условии, что остаточная дисперсия совпадает с величиной остаточной дисперсии для множественной регрессии. Влияние фактора х, статистически значимо, так как F = 22,0 больше табличного значения /табл = 4,21. Третье значение F = 16,5 — это частный /"-критерий, оценивающий значимость дополнительного включения в модель фактора х2 после введения в нее фактора х,. Его величина совпадает с ранее рассчитанной по формуле частного /"-критерия Fxr [c.134]
Если А является наивысшим порядком расчета частных коэффициентов корреляции для уравнения регрессии, то практически величина к совпадает с числом степеней свободы для остаточной вариации с п — т — 1. Так, в уравнении = а + Ьх х + b2 х2 + Ьъ х х д 3 + е, рассчитанном при п = 30, я — т — 1 = 26. Если же уравнение рефессии дополняется расчетом частных коэффициентов корреляции разных порядков (второго, третьего и т. п.), то [c.140]
Взаимосвязь показателей частного коэффициента корреляции, частного /"-критерия и 7-критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов. Отсев факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинам tb. и Fx.. Частный /"-критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом. [c.141]
Применение зяблевой вспышки способствует росту урожайности в среднем на 2,9 ц с 1 га при одном и том же количестве внесенного удобрения на 1 га, что в целом соответствует и различию средней урожайности по видам вспашки (15,3 ц с 1 га для зяблевой вспашки и 12,5 ц с 1 га для весенней вспашки). Частный /"-критерий для фактора z составил 16,58, что выше табличного значения при числе степеней свободы 1 и 22 (4,30 при а = 0,05 и 7,94 при а = 0,01). Это подтверждает целесообразность включения фиктивной переменной в уравнение регрессии. [c.145]
Поэтому вполне реально предположить единую меру влияния данного фактора независимо от вида вспашки, что и имеет место в уравнении регрессии с фиктивной переменной. Включив фиктивную переменную, удалось измерить ее влияние на изменение урожайности частный коэффициент корреляции ryz. х, оценивающий в чистом виде влияние данного фактора, составил 0,6555, что несколько выше, чем аналогичный показатель для фактора х, т.е. г = 0,6385. [c.146]
Результаты свидетельствуют о целесообразности построения модели по отдельным частным совокупностям. Ввиду разной зависимости уровня квалификации рабочих от уровня занятости ручным трудом по заводам с традиционной и прогрессивной технологиями производства уравнение регрессии по совокупности в целом не позволило выявить наличие связи. Не улучшился результат модели и с введением фиктивной переменной, ибо этот метод предполагает равенство коэффициентов регрессии при х по частным совокупностям и возможность их замены общим коэффициентом регрессии Ь. [c.149]
Управляемый фактор 371 Управляющая информация 413 Управляющая система 371 Управляющее воздействие 371 Управляющие параметры 258, 371 Уравнение обмена 372 Уравнение отклика 251 Уравнение регрессии 305 Уравнения бюджета потребителей 152 Уравнения в частных производных [c.493]
В частном случае единственного результирующего признака у и F - класса линейных функций получаем линейное уравнение регрессии [c.285]
Для выявления резервов снижения себестоимости более применимы уравнения регрессии, определяющие частные зависимости х от какого-либо фактора [c.227]
Если поверхность отклика локально может быть описана линейным уравнением, то частные производные, очевидно, будут равны коэффициентам уравнения регрессии [c.271]
Имеется три явления А, В и С, связанные между собой необходимо рассчитать силу связи между А и В при условии исключения воздействия явления С (как посредника между А и В). Для этого, зная уравнения регрессии между А и С и между В и С , рассчитываются для каждой пары А и В те их значения (наиболее вероятные), к-рые они принимали бы, если бы значения С оставались постоянными (напр., равными средней величине). Тогда, вычисляя К. к. между преобразованными переменными Ас и Вс, можно уловить ту частную связь между А и В [c.275]
Частный Значимость частного коэффициента регрессии переменной/можно проверить, используя приростную Она основана на приращении в объясняемой сумме квадратов, полученном добавлением независимой переменной в уравнение регрессии после исключения всех других независимых переменных. [c.660]
Логически, зависимость между коэффициентом парной регрессии и частным коэффициентом регрессии можно проиллюстрировать образом. Предположим, что мы исключили эффект от влияния Это можно сделать, установив регрессию по Иначе говоря, можно воспользоваться уравнением а + и вычислить остаточный член = (X, — Тогда частный коэффициент регрессии. станет равным коэффициенту парной регрессии полученному из уравнения 7 =а Таким образом, частный коэффициент регрессии равен/1, коэффициенту парной регрессии между переменной Уи остаточным значением переменной [c.661]
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности1 [c.110]
При Т — 1, Тп — 2 при помощи прямого обучения по алгоритму МГУА находится уравнение регрессии для ошибки, например Дх0 — f(Ax l,Ax 2,x l,x 2). Затем строится кривая Ax(t) для каждого частного уравнения регрессии. [c.60]
В эконометрике частные коэффициенты корреляции обычно не имеют самостоятельного значения. В основном их используют на стадии формирования модели, в частности в процедуре отсева факторов. Так, строя многофакторную модель, например, методом исключения переменных, на первом шаге определяется уравнение рефессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. На втором шаге отбирается фактор с наименьшей и несущественной по f-критерию Стьюдента величиной показателя частной корреляции. Исключив его из модели, строится новое уравнение регрессии. Процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля. Если исключен несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построения рефессионной модели почти не отличаются друг от друга, т. е. R2p + j R2p где р — число факторов. [c.128]
Оцените статистическую значимость уравнений регрессии и их параметров при помощи F-критерия Фишера-Снедекора, частных F-критериев и t-критерия Стьюдента. [c.10]
Для анализа взаимосвязи или связи экономических показателей приходится обращаться к совокупности статистических параметров средних величин, средних квадрати-ческих отклонений, параметров распределения, парных и частных коэффициентов корреляции, коэффициентов влияния, корреляционных отношений, параметров уравнений регрессии, остаточных дисперсий, множественных коэффициентов корреляции и множественных корреляционных отношений. Для краткости совокупность статистических параметров, описывающих множество экономических показателей и взаимосвязь между ними, мы называем экономико-статистической моделью. [c.12]
| Рисунок 17.4. Объем реального частного потребления в США ( ONS, млрд.долл., 1982 г.) в 1971-1990 гг фактический и оцененный по уравнению регрессии. Отклонения от линии регрессии | 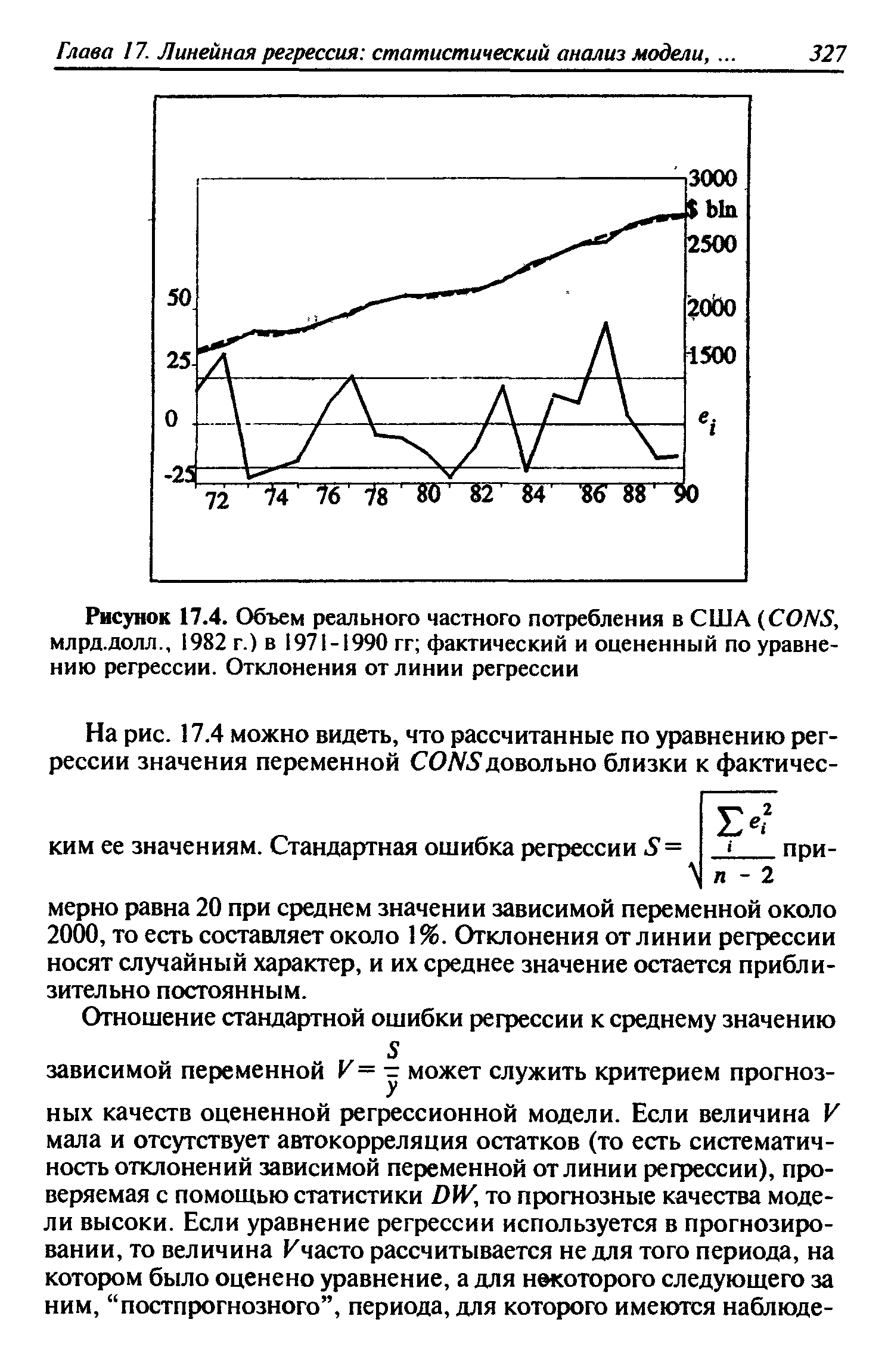 |
