При задании в модели банка непрерывного времени состояние j-й характеристики может рассматриваться как значение функции %j(t), определенной на множестве Ги принимающей значения из множества R[. Тогда графику (г) играет роль траектории изменения во време-ни -й характеристики. Соответственно, состояние банка в целом есть значение векторной функции от времени [c.146]
Необходимо отметить, что формирование математической модели принятия решений (т. е. построение множества X и векторного критерия /) нередко представляет собой сложный процесс, в котором тесно взаимодействуют специалисты двух сторон. А именно, представители конкретной области знаний, к которой относится исследуемая проблема, и специалисты по принятию решений (математики). С одной стороны, следует учесть все важнейшие черты и детали реальной задачи, а с другой — построенная модель не должна оказаться чрезмерно сложной для того, чтобы для ее исследования и решения можно было успешно применить разработанный к настоящему времени математический аппарат. Именно поэтому этап построения математической модели в значительной степени зависит от опыта, интуиции и искусства исследователей обеих сторон. Его невозможно отождествить с простым формальным применением уже известных, хорошо описанных алгоритмов. [c.19]
Эколого-математическая модель, например, может быть представлена в виде иконографической модели — схемы модели объекта (рис. 1.1) и в виде функциональной зависимости состояния объекта Ф(0 =Л С A, G, Y, Q, f), которая является функцией времени от входных факторов состояния объекта, состояния управления, выходных факторов и факторов внешней среды. При этом все факторы следует рассматривать в данном случае в виде векторных величин, изменяющихся с течением времени. При моделировании подобного объекта могут быть применены различного вида модели для исследования тех или иных его частей с различным целевым назначением. [c.9]
Векторная транспортная масса — пространственно-временная информация об источнике и стоке (пункте назначения), а в некотором случае и об определенном моменте времени перевозки. [c.43]
ТЭО-ИНВЕСТ" проведет вычисления и построит (или обновит) графики выходных показателей. На графиках со скалярными параметрами (IRR и NPV) отображается зависимость этого параметра от изменения входной переменной, например IRR (цена). На графиках с векторными параметрами (расчетный счет, чистая прибыль и др.) отображаются семь временных зависимостей этих параметров, соответствующих одному из уровней изменения входной переменной, например чистая прибыль (цена продукции). [c.198]
Чтобы полностью задать движение во времени соотношения спроса и предложения, необходимо знать его фазовое состояние х0 = (х 0, х"0) в начальный момент времени и выбрать векторную функцию и (t) для t > t0. [c.87]
Функционирование системы во времени характеризуется появлением входных, выходных сигналов и изменением состояний в векторных пространствах входных, выходных сигналов и состояний. [c.21]
Экономическая система находится в статическом состоянии, если ее параметры меняются в течение некоторого времени, но сохраняется тенденция возвращения в исходное состояние. Классическим примером такой модели является простое воспроизводство. Развитие же экономической системы предполагает ее переход в качественно новое состояние. Динамика рыночной экономики изучается в рамках теорий роста и цикла. Теория роста исследует факторы и условия устойчивого развития как долговременной тенденции, т.е. можно говорить о векторной направленности движения системы. Теория цикла призвана объяснить причины колебаний конъюнктуры во времени, т.е. акцент смещается в сторону анализа волнообразного характера развития. [c.192]
Принцип согласованности. При оценке эффективности проекта используемые показатели (и информация) должны согласовываться по ряду условий, в том числе иерархически (см. пример 3.1), по времени, цели, структуре и т. д. Так, по степени структурированности (т. е. по характеру описания альтернатив и предпочтений участников) проекты можно разделить на "хорошо структурированные", "слабо структурированные" и "неструктурированные". В зависимости от этого выбираются формализованные скалярные и векторные, или неформализованные, экспертные критерии и процедуры оценки. Предполагается и учет социальной значимости проектов. В этой связи их можно разделить на "значимые" и "малозначимые". Кроме [c.48]
Данный пакет позволяет решать типовые задачи статистического анализа и построения эмпирических моделей следующих разделов математической статистики и теории вероятностей преобразование данных статистические характеристики и их оценки законы распределения порядковые статистики статистическая проверка гипотез корреляционный анализ анализ временных рядов построение эмпирических моделей с одной и многими независимыми переменными, в том числе моделей со случайными переменными, нелинейных относительно параметров и с ограничениями на параметры, векторных и динамических моделей оценка линейных моделей, в том числе оценка параметров и доверительных интервалов параметров моделей и зависимой переменной, анализ остатков, прогнозирование зависимой переменной, решение динамических моделей. [c.180]
Под информационной технологией предполагается понимать векторный процесс сжатия информации в пространстве и времени, использующий специфические способности человека по ее восприятию и принятию решения в неопределенной ситуации. С изменением понятия информационной технологии появляется необходимость определения новых свойств информации [c.141]
В перспективе под информационной технологией предполагается понимать векторный процесс сжатия информации в пространстве и времени, использующий специфические способности человека по ее восприятию и принятию решения в неопределенной ситуации. [c.144]
В этой связи при обосновании решений прежде всего стремятся выяснить, нельзя ли свести исходную общую задачу к более простому, частному виду. Например, концептуальные частные критерии в ИСС могут иметь настолько сильное различие в важности, что, по сути, задача сводится к оценке вариантов решений только по одному из них. Иногда частные критерии эффекта, затрат и времени некоторым "естественным" образом агрегируются в скалярную функцию, либо исходная задача с векторным результатом может быть представлена как бы скалярной, если значения всех частных результатов кроме одного слабо варьируются по альтернативам. 3 подобной ситуации разумно задачу с векторным критерием аппроксимировать задачей со скалярным критерием. Бывает, что информация об относительной важности частных критериев позволяет заранее определить способ решения задачи через какие-то вспомогательные скалярные критерии. Нередко множество альтернатив является дискретным, что также значительно упрощает поиск наилучшего решения. [c.155]
В отличие от задач обоснования решений по скалярному критерию, результатом решения которых является оптимальная в рамках соответствующей модели альтернатива, в задачах с векторным критерием нельзя с абсолютной уверенностью утверждать, что то или иное решение действительно (объективно) оптимально. Один из вариантов решения может превосходить другой по одним критериям и уступать по другим (другому) критериям. Следовательно, объективно утверждать, что какое-то из двух решений в указанных условиях лучше другого, не представляется возможным. Только со временем будет объективно ясно, сколь верным было приня- [c.168]
Если все процессы-компоненты векторного процесса являются вполне определенными, то для каждого из них в любой момент времени определяется понятие будущего (накопленного), а также дисконтированного значений сумм и событий. [c.72]
Информационный процесс W определен как векторный стохастический процесс с дискретным временем. Конечная выборка из его траекторий удобно представляется в виде дерева сценариев каждый сценарий соответствует траектории процесса [c.33]
Рассмотрим далее модели финансового рынка в дискретном времени. Для этого рассмотрим векторно-матричное дифференциальное уравнение(7.3.5). [c.175]
Векторно-матричное разностное уравнение, описывающее процесс функционирования финансового рынка в дискретном времени с учётом результатов раздела 7.2.2 может быть представлено в виде [c.183]
| Рис. 7.7. Математическая модель финансового рынка в дискретном времени в виде формирующего фильтра векторного случайного процесса. | 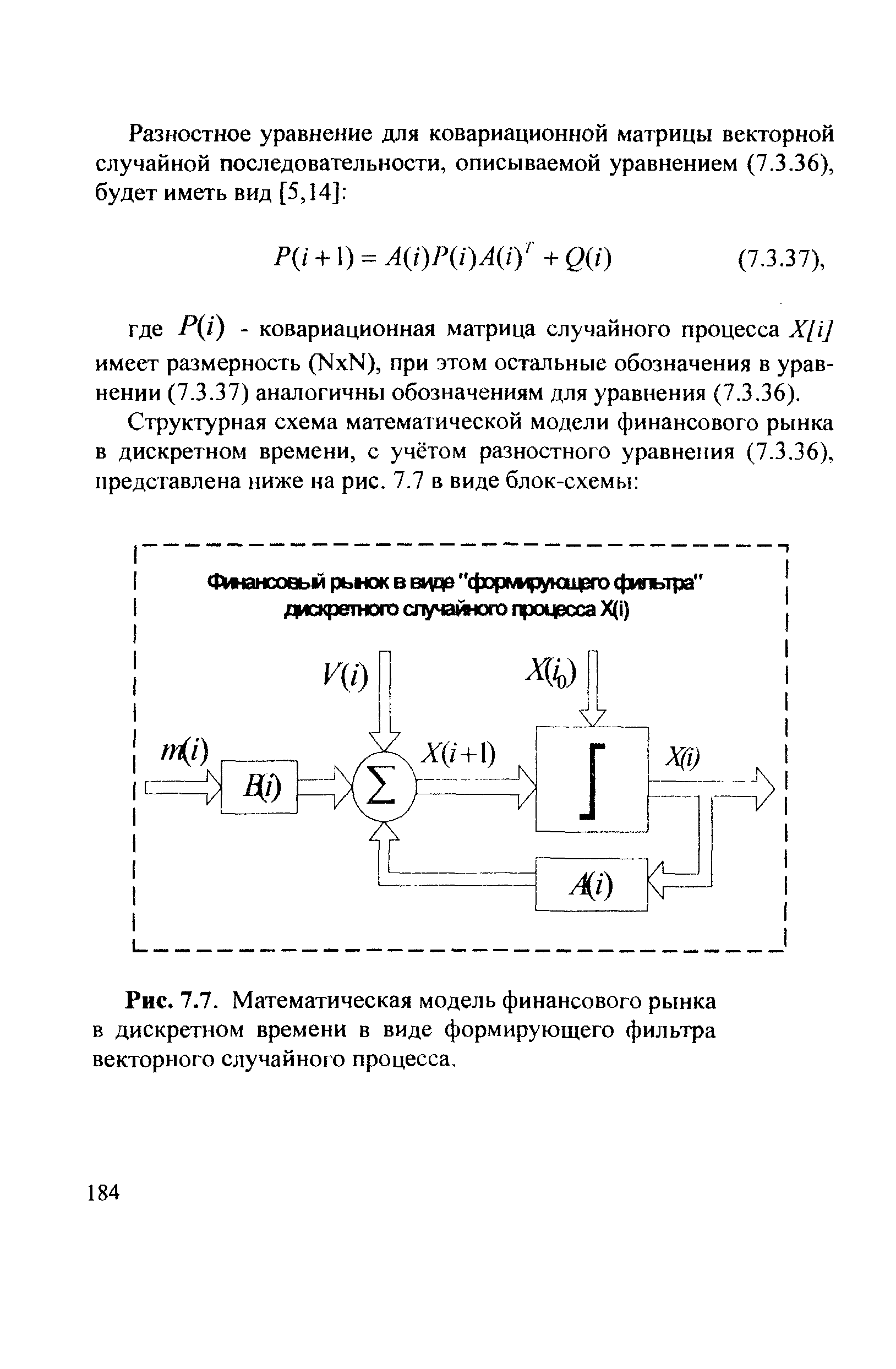 |
Настоящая книга является дополнением к ранее изданным публикациям автора "Эконометрика для начинающих Основные понятия, элементарные методы, границы применимости, интерпретация результатов" (2000), "Эконометрика Основные понятия и введение в регрессионный анализ временных рядов" (2004). В ней рассматриваются методы статистического анализа моделей с дискретными объясняющими переменными, систем одновременных уравнений, панельных данных, а также структурные и приведенные формы векторных авторегрессий и моделей коррекции ошибок. [c.7]
Временные ряды — основной источник данных для построения эконометрических моделей в форме систем одновременных уравнений. Однако методы построения структурных моделей (особенно крупных моделей, содержащих большое количество уравнений и переменных) достаточно сложны, поэтому в последние десятилетия был разработан и получил широкое распространение еще один подход — построение моделей векторной авторегрессии. В разработку этого подхода внесли большой вклад Р. Лукас, Т. Сарджент, К. Симе и ряд других макроэкономистов. [c.330]
В случае с многими переменными может быть больше одного вектора коинтеграции. Следовательно, нужна методология, которая бы определила структуру всех векторов коинтеграции. Такой процесс был разработан Йохансеном (1988) и Йохансеном и Йезулиусом (1990). Он определяет множество временных рядов в качестве векторного авторегрессионного (VAR) процесса. Модель исправления ошибки разрабатывается следующим образом. [c.344]
В системе АРИУС объект управления рассматривается как взаимодействующая совокупность предметов и процессов, называемая объектной системой. Потоки информации, например, отражают движение объектной системы. АРИУС ориентирован на фиксацию в каждый дискрет времени состояния объектной системы, характеризующей ретроспективу, настоящее и перспективу развития объекта. Каждый класс фиксируемых предметов или процессов ставится в однозначное соответствие с некоторой конструкцией, называемой структурным компонентом информационного отображения объекта. В- системах обработки данных структурным компонентам соответствуют массивы значений их характеристик и признаков. Такие массивы в АРИУС имеют структуру таблиц. Элементы объектной системы могут иметь векторную характеристику. [c.50]
Совокупность ограничений на состояния и управления для каждого периода [ , + ] в векторной форме принимает вид G (t, )>0, t = 0,1,..., Т. В каждый момент времени t агрегат "внешняя среда и система" находится в состояниях из фазового множества E(t, U). Например, если реконструкция или строительство объекта осуществляется за один период [t, t+l], то переход системы (агрегата) из произвольного состояния i
Векторная компьютерная графика до недавнего времени имела довольно ограниченное применение и основывалась на методах, используемых программистами для подготовки простых рисунков, состоящих из точек, прямых линий и областей, закрашенных однотонным цветом. Однако с развитием компьютерных дизайн-технологий изобразительные возможности векторной графики намного расширились. Сегодня лучшие образцы векторной графики почти так же реалистичны, как и фотографические изображения, а по своим потенциальным возможностям они намного превосходят растровую графику. [c.141]
Для преобразования растровых изображений в векторные используются программы-конверторы типа orelTra e, получившие название программ векторизации изображений. Векторизация растровых изображений - процесс достаточно сложный, для которого необходимы специальные знания в области обработки компьютерной графики. Он требует значительных вычислительных ресурсов компьютера и затрат времени, однако векторизованные рисунки можно как угодно вращать, масштабировать и преобразовывать, используя при этом все преимущества векторной графики. [c.227]
Путь к терминальным ветвям ИСС, где будут располагаться имена частных компонентов векторного результата, проходит на рис. 2.2 через обобщенные семантические характеристики с именами "Эффект", "Затраты", "Время". Далее эти характеристики уточняют ("увеличиваем масштаб исследования"), а дерево разворачивается вниз. Например, "Эффект" декомпозируем на такие составляющие, как "Изменения в свойствах, составе или структуре объектов" и "Изменения во взглядах, впечатлениях, суждениях, мнениях, предпочтениях субъекта". Концептуальный критерий "Затраты" расчленяем по составляющим "Материальные" и "Психологические" относительно временных свойств исхода интересуемся временами "Принятия решения", "Начала первых изменений" или "Завершения операции" и т. д. Стрелки внизу условно показывают, что подобные уточнения понятий и ветвления дерева могут проводиться до тех пор, пока этого требует проблемная ситуация для принятия ЛПР окончательного решения относительно имен частных компонентов вектор- [c.151]
Основная причина того, что в финансовой математике при рассмотрении моделей с непрерывным временем ограничиваются, главным образом, классом семимартингалов, состоит в том, что для них есть, как мы видим, понятие (векторного) стохастического интеграла, с помощью которого определяется эволюция капитала и дается понятие самофинансируемости. (Это обстоятельство было с полной отчетливостью отмечено в работах М. Харрисона, Л. Крепса и С. Плиски, [214] и [215], впервые обративших внимание на роль семимартингалов и стохастического исчисления для них при описании динамики цен активов.) [c.307]
Другое дело - случай непрерывного времени, где уже для формулирования свойства самофинансируемости приходится прибегать к векторным [c.317]
В финансовой практике нередко встречаются случаи, когда одновременно рассматривается несколько финансовых процессов в рамках некоторого общего процесса. В частности, такая ситуация возникает, например, при открытии инвестором нескольких сберегательных счетов в одном или различных банках, при формировании портфеля инвестиционных активов и т.п. Действительно, если инвестор покупает несколько акций, то вложение средств в отдельную акцию (как и открытие отдельного вклада) можно рассматривать как отдельный процесс (микропроцесс) в рамках общего портфельного процесса. Эти отдельные процессы представляют собой компоненты общего ( векторного ) процесса. Здесь важно, что в течение определенного времени (пока сохраняется структура компонент процесса) можно говорить о состояниях процессов- компонент. При этом вполне возможно, что разные компоненты могут запускаться в разные моменты времени. Иными словами, вполне допустимо, чтобы k-и процесс имел [c.71]
Для генерации сценариев в большинстве случаев используется модел векторной авторегрессии (ВАР) [54]. Стандартные модели ВАР расширяются для моделирования смены экономических режимов (например, высокая инф ляция в 1970-х годах и относительно низкая в 80- и 90-х годах). Кроме этого в модели ВАР учитываются соотношения рыночного равновесия моделирует ся приближение рынка к равновесному состоянию с течением времени. Для каждого сценария развития экономической ситуации оценивается соответству ющий объем пенсионных выплат. Для моделирования изменения статуса каж дого из участников фонда используется управляемая цепь Маркова (каждьк из участников фонда может уйти в отставку, умереть, прекратить участие i фонде, получить повышение или понижение по службе возможен приход i фонд новых участников). [c.730]
