Отметим, что методы линейного программирования исполь-дуются в настоящее время и для решения задач оптимизации в нелинейных моделях с нелинейными критериями. При этом осуществляется линеаризация соотношений модели в окрестности текущей точки и переход к новой точке с использованием результатов решения задачи линейного программирования. [c.58]
Если метод ЛИФО позволяет занижать прибыль, то в результате расчетов по методу ФИФО прибыль оказывается значительно завышенной, особенно в условиях инфляции. Применение этих методов требует линеаризации операций, так как материальные ресурсы оцениваются не только по видам, но и по датам и партиям поступления. [c.228]
В качестве основы линеаризации можно использовать приближение нелинейных зависимостей некоторыми простыми функциями [92]. В данном случае наиболее подходящей формой аппроксимирующего полинома является ступенчатая функция (рис. 39, на котором качественно изображен график характерного нелинейного норматива и его аппроксимация). Остановимся несколько подробней на ступенчатой аппроксимации. Пусть функция Я (а) определена на отрезке [аЪ] и имеет вид, изображенный на рис. 43. [c.224]
Сложным источником дохода можно назвать источник, доход которого является некоторой функцией нескольких случайных величин. Риск получения дохода из такого источника может быть оценен, как указано в главе 4, на основе линеаризации функции случайных аргументов. Напомним, что числовые характеристики функции случайных аргументов определяют путем разложения в ряд Тейлора. Обычно используют линейные приближения характеристик. Линейные оценки для связанных случайных аргументов имеют вид [c.123]
Легко видеть, что эти уравнения, по существу, те же, что и для линейной связи. Линеаризация гиперболического уравнения достигается заменой 1х на новую переменную, которую можно обозначить z. Тогда уравнение (8.27) примет вид у = а + bz. Это и следует сделать, вычисляя гиперболу на компьютере, если программа для него не предусматривает автоматического вычисления гиперболических регрессий. [c.267]
Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Нелинейные формы зависимости приводятся к линейным путем линеаризации. [c.117]
В главе 5 рассмотрен ряд проблем, связанных с использованием регрессионных моделей, таких, как мультиколлинеарность, фиктивные переменные, линеаризация модели, частная корреляция. [c.4]
Основная задача, решаемая на этом этапе, — выбор вида функции f(X) в эконометрической модели (1.1), в частности, возможность использования линейной модели как наиболее простой и надежной (о некоторых вопросах линеаризации модели см. 5.5). Весьма важной проблемой на этом (и предыдущих) этапе эконометрического моделирования является проблема спецификации модели (см. гл. 10), в частности выражение в математической форме обнаруженных связей и соотношений установление состава экзогенных и эндогенных переменных, в том числе лаговых формулировка исходных предпосылок и ограничений модели. От того, насколько удачно решена проблема спецификации модели, в значительной степени зависит успех всего эконометрического моделирования. [c.22]
В предыдущих главах была изучена классическая линейная модель регрессии, приведена оценка параметров модели и проверка статистических гипотез о регрессии. Однако мы не касались некоторых проблем, связанных с практическим использованием модели множественной регрессии. К их числу относятся мультиколлинеарность, ее причины и методы устранения использование фиктивных переменных при включении в регрессионную модель качественных объясняющих переменных, линеаризация модели, вопросы частной корреляции между переменными. Изучению указанных проблем посвящена данная глава. [c.108]
Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными. [c.125]
Для линеаризации модели в рамках первого подхода могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам. [c.125]
В случае, если функция ДО нелинейная и не представляется возможным применить методы линеаризации модели ( 5.5), то параметры тренда находят из соответствующих (в зависимости от вида функции flj)) систем нормальных уравнений, которые здесь не приводятся (см., например, [17]), либо с помощью специальных процедур оценивания. [c.141]
Лаговая переменная 20, 147, 178 Линеаризация модели 22, 125, 126 Линейная комбинация векторов 270 [c.301]
Учитывая, что погрешность технико-экономической и геолого-промысловой информации при решении оптимизационных задач развития и реконструкции ЕГС заведомо находится в пределах 5 — 10%, при линеаризации функции [c.71]
Возможная схема линеаризации модели оптимизационного блока. При учете замечаний 2 и 3 относительно возможности сведения решения нелинейной от параметра 6,- 8 модели к группе линейных трудность поиска оптимального плана исходной модели определяется нелинейностью функционала. [c.115]
Приближенное значение IRR можно найти, заменив кривую NPV прямой, т.е. линеаризацией функции NPV от ставки процента. Это можно сделать применив известное из аналитической геометрии уравнение прямой, построенной по двум точкам [c.152]
Эквивалентная линеаризация, осуществляемая предварительно или в ходе решения, позволяет представить (2.54), (2.55) следующим образом т [c.45]
Процедуры линеаризации в обоих типах моделей вынесены за пределы формального описания. [c.48]
Линеаризация может быть осуществлена и за счет замены [c.204]
Построению степенной модели у = а хь предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения [c.12]
Парабола второй степени, как и полином более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадет с индексом корреляции Ryx = ryv где z — преобразованная величина [c.81]
Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время / = 1,2,..., я, а в качестве зависимой переменной — фактические уровни временного ряда у,. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации. [c.234]
Лаг 19, 230, 291, 293, 297, 307, 309 Лаговые переменные 291, 307, 311 Линеаризация 62-63, 66, 69-71, 103 Линейная модель множественной регрессии 90 Линейность 15-16, 70-71 Ложная корреляция 19, 222 [c.339]
Я (У ) = - "(Y ), поэтому линеаризация выглядит следующим [c.82]
| Рис. 29. Линеаризация вогнутой функции | 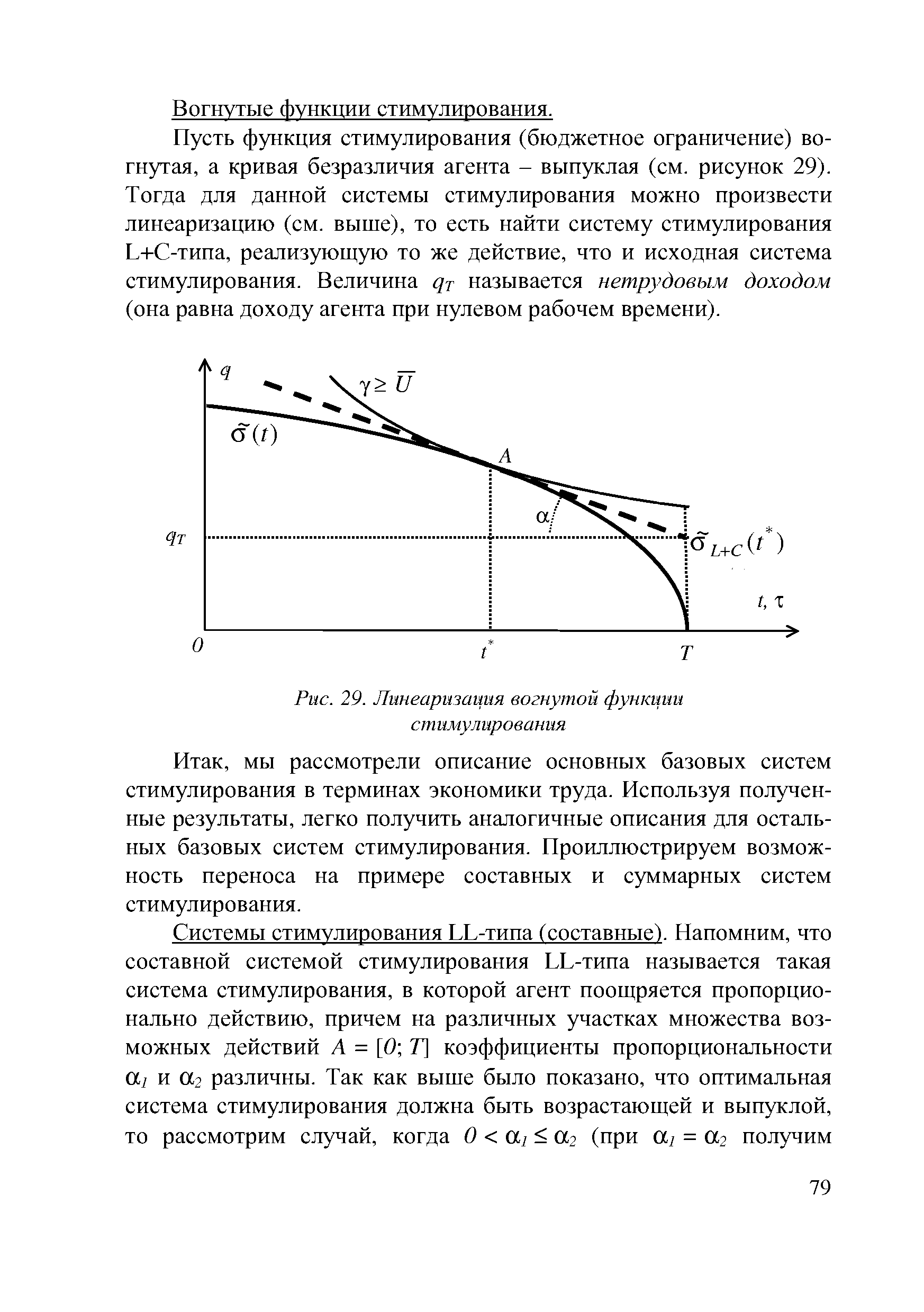 |
При такой постановке задачи оптимизации плана производства НПЗ модель (2)— (9) является нелинейной. Аналогичные постановки имели место в работах [2, 3, 4,. Б]. Пути решения указанных задач в основном связываются с различными методами линеаризации, предложенными в работе Дж, Данцига 16]. Подробное обоснование этих методов в отношении моделей оптимизации плана производства НПЗ рассматривается в работах [3, 4]. Недостатками методов линеаризации является, во-первых, значительное увеличение размерности моделей, а во-вторых, усложнение подготов-.ки исходной информации для решения. [c.98]
Разработаны приемы расчета /RR, в том числе компьютерные, основанные на итеративном приближении при помощи линеаризации к точке г. Ряд электронных таблиц (например, программный пакет Lotus И 23) позволяет, задав местоположение денежного потока, исчислить соответствующие значения NPV (при известной г) и /RR. [c.150]
Возможная схема линеаризации оптимизационного блока. Для задач типа (150)—(158) не разработаны точные методы решения. При учете замечаний относительно возможности освобождения модели от нелинейности по Qijs трудность ее решения определяется нелинейностью функционала. Вопрос о том, в каких случаях необходимо учитывать нелинейную составляющую и когда ею можно пренебречь, должен решаться особо в каждой конкретной ситуации. При этом следует иметь в виду, что, с одной стороны, неправомерное пренебрежение нелинейностью приводит к неадекватности модели реальным условиям, а следовательно, и к неверным решениям. С другой же стороны, чрезмерное уточнение исходных данных (нормативов) приводит к усложнению задачи и затрудняет ее численную реализацию. Очевидно, что для месторождений, имеющих малые площади (и, следовательно, на большие значения Nijs). Нелинейностью нормативов можно пренебречь, используя при этом усредненные значения нормативов. [c.223]
Решение системы алгебраических уравнений модели осуществляется с использованием метода линеаризации. При проведении расчета режимов работы технологической линии УНТС составляется и последовательно решается система уравнений тепловых балансов и теплопередач, относящихся к сепараторам С-1 и С-2, теплообменнику Т-1 и дросселю, с постепенным уточ- [c.117]
Линеаризация функции случайных аргументов. В общем случае числовые характеристики произвольной функции случайных аргументов определяются путем разложения в ряд Тейлора. Обычно используют линейные приближения оценок числовых характеристик, при необходимости их можно уточнить, вычисляя члены ряда Тейлора высших порядков. Линейные оценки для независимых случайных аргументов имеют вид12 [c.46]
В учебнике излагаются основы эконометрики. Большое внимание уделяется классической (парной и множественной) и обобщенной моделям линейной регрессии, классическому и обобщенному методам наименьших квадратов, анализу временных рядов и систем одновременных уравнений. Обсуждаются различные аспекты многомерной регрессии мультиколлине-арность, фиктивные переменные, спецификация и линеаризация модели, частная корреляция. Учебный материал сопровождается достаточным числом решенных задач и задач для самостоятельной работы. [c.2]
Изображенное на рис. 10.3 семейство гипербол было получено nyrei искусственной линеаризации зависимостей A /A Q и Р/ /А. тоб) проследить принципиальную взаимосвязь между At и PL. Для каждого кон кретного случая это функция, близкая к гиперболической, с асимптотой являющейся отношением приростов PI. ( ) к Aff). [c.212]
Более точное значение внутренней нормы доходности можно найти, сближая концы отрезка. Разработаны компьютерные приемы расчета IRR, в том числе основанные на итеративном приближении с помощью линеаризации к точке г. Ряд электронных таблиц (например, программный пакет Lotus 123, Ex el, QPRO) позволяет, задав "местоположение" денежного потока, исчислить соответствующее значение NPV (при известной г) и IRR. [c.154]
С точки зрения математической корректности эквивалентного преобразования и технологической интерпретации модели и ее решения, представляют интерес методы линеаризации, основанные на принципе разложения варьируемых векторов //(") технологических коэффициентов я,-Дм) по вершинам выпуклых многогранников PJ, заданных ограничениями (2.21). Коэффициент аг-Дм)еС/- при этом может быть определен через координаты - = qj, a2q/< > anqj вершин выпуклого многогранника PJ-. [c.29]
В моделях с переменными параметрами, допускающих в некоторых случаях эффективную линеаризацию, в зависимости от алгоритма решения предусмотрена 1) генерация аппроксимационных вариантов, осуществляемая по ходу реализации алгоритма решения, или 2) предварительное определение множества аппроксимирующих вариантов путем разложения варьируемых векторов технологических параметров по вершинам выпуклых многогранников, определяющих допустимые области технологических параметров. [c.43]
Следует также отметить, что алгоритмы решения задач с переменными параметрами имеют дос аточно сложный вид, связанный с громоздкостью процедур линеаризации при большом числе варьируемых способов производства. [c.44]
Смотреть страницы где упоминается термин Линеаризация
: [c.99] [c.269] [c.73] [c.13] [c.90] [c.82] [c.83] [c.54] [c.54] [c.79] [c.82] [c.97]Экономико-математический словарь Изд.5 (2003) -- [ c.168 ]
Прикладная статистика Исследование зависимостей (1985) -- [ c.184 ]
