Оценка адекватности модели и существенности параметров линейной [c.7]
| Таблица 2.1.14 Промежуточные расчеты для оценки адекватности модели | 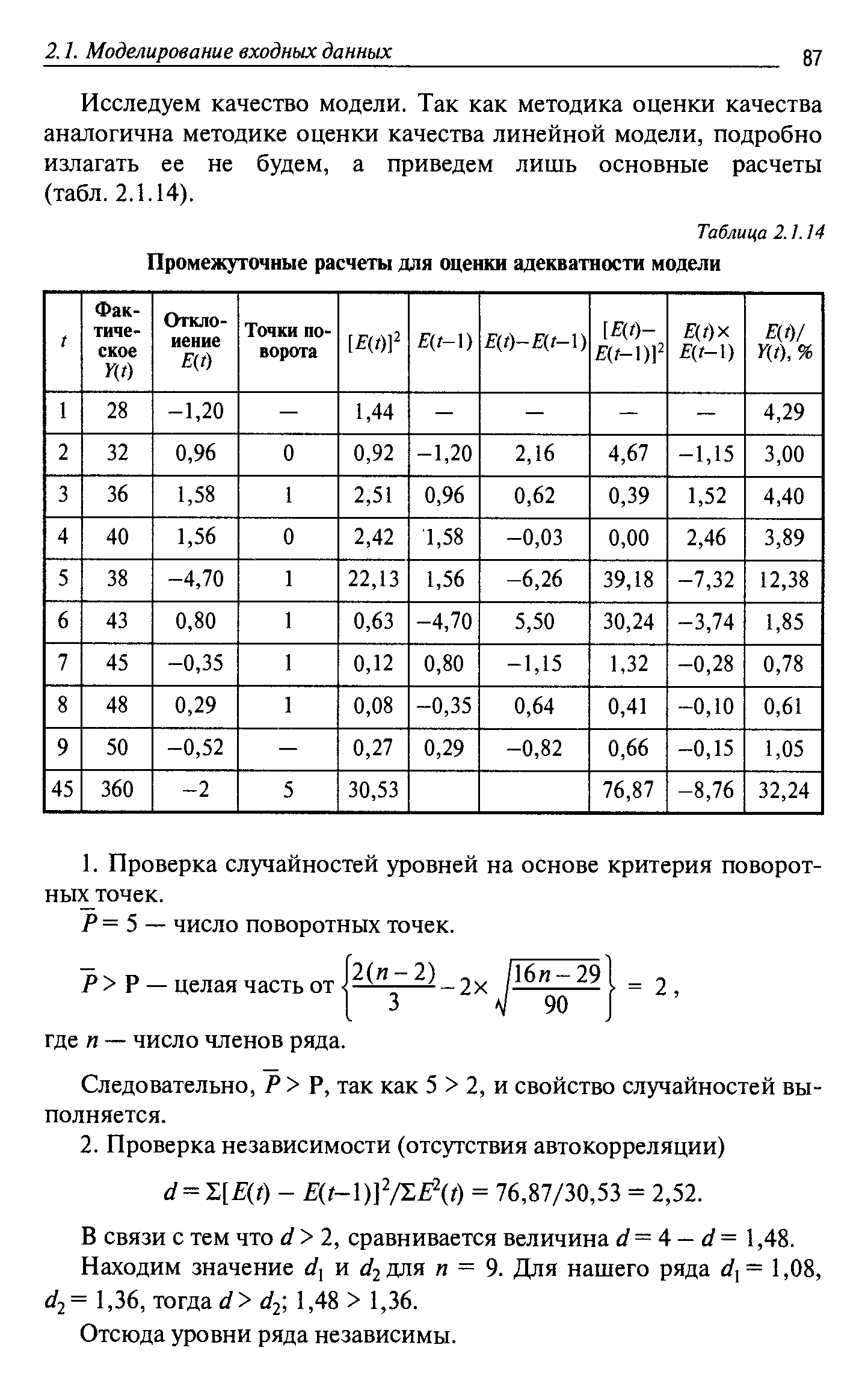 |
Оценка адекватности модели. Располагая ошибкой опыта, мы можем выяснить, является ли линейная модель адекватной. Для проверки адекватности строят F-критерий Фишера. Им проверяют гипотезу о том, что дисперсия относительно модели значимо превышает дисперсию опыта против альтернативы о незначимом различии между этими дисперсиями. Если различие незначимо (при некотором уровне значимости, обычно 5%-ном), то гипотеза об адекватности модели может [c.230]
Оценка значимости коэффициентов. Оценка адекватности модели служит основой для того, чтобы принимать дальнейшие решения, однако всегда дают также и оценку значимости коэффициентов. Она важна при интерпретации модели и для дальнейшего отсеивания [c.231]
Оценка адекватности модели. Располагая ошибкой опыта, мы можем выяснить, является ли линейная модель адекватной. Для проверки адекватности строят F-критерий Фишера. [c.238]
Оценка значимости коэффициентов. Оценка адекватности модели служит основой для того, чтобы принимать дальнейшие решения, однако всегда дают также и оценку значимости коэффициентов. [c.238]
Количественную оценку адекватности модели объекту исследования проводят для случая, когда можно определить значения отклика системы в ходе натурных испытаний. [c.402]
Если возможность измерения отклика реальной системы отсутствует, оценку адекватности модели проводят на основе субъективного суждения соответствующего должностного лица о возможности использования результатов, полученных с использованием этой модели, при выполнении им служебных обязанностей (особенно — при обосновании решений). По сути, в этом случае, как уже отмечалось в п. 1.3.4, неформальная процедура проверки адекватности модели направлена на повышение степени доверия ЛПР к результатам моделирования и желания пользоваться ими. [c.403]
Необходимый этап построения модели — проверка ее достоверности. Естественно, что чем лучше модель отражает реальность, тем выше ее потенциал как средства принятия хорошего решения. Но главное в оценке адекватности модели заключается в том, получены или нет ответы на вопросы, поставленные перед ней менеджером, соответствовала ли она целям моделирования. Хороший способ проверки модели — это опробование ее на ситуациях из ближайшего прошлого (если есть уверенность, что ни набор, ни степень, ни направление влияния факторов не изменились). [c.72]
Оценка адекватности модели [c.29]
Такого процесса, как испытание правильности модели, не существует. Вместо этого экспериментатор в ходе разработки модели должен провести серию проверок с тем, чтобы укрепить свое доверие к модели. Оценка адекватности модели заключается в повышении до приемлемого уровня степени уверенности, с которой можно судить относительно корректности выводов о реальной системе, полученных на основании обращения к модели. [c.30]
Таким образом, вопрос оценки адекватности модели имеет две стороны [c.31]
Оценка адекватности моделей по числу превышений [c.655]
Оценка полученной модели по статистическим характеристикам показывает, что колеблемость затрат исследуемой подсистемы на 85 % обусловлена колеблемостью факторов, включенных в модель, коэффициент множественной корреляции высокий (/ = 0,92) и существенный (f = = 39,8), модель является адекватной, средняя ошибка аппроксимации (ё = 5,7%) меньше 10%. [c.39]
Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, (или, как [c.74]
В З.б был введен коэффициент детерминации / 2 как одна из наиболее эффективных оценок адекватности регрессионной модели, мера качества уравнения регрессии, характеристика его прогностической силы. [c.103]
Статистическая оценка полученной модели в целом показала, что она адекватна изучаемому явлению (фактическое значение F-критерия равно 3,87, при табличном значении 1,44), [c.195]
Другой недостаток моделей векторной авторегрессии — необходимость принятия решения относительно величины лага, адекватных методов оценки параметров модели, поскольку обычный МНК, как было показано выше, чаще всего неприменим при оценке параметров моделей с распределенным лагом и тем более неприменим для оценки параметров моделей авторегрессии. Поэтому методы оценки параметров моделей VAR очень громоздки, и в настоящее время далеко не все статистические пакеты прикладных программ имеют эту функцию. Однако в целом модели VAR потенциально значительно проще структурных моделей. [c.332]
В этом случае для построения адекватной модели оценки риска [c.103]
Моделирование систем на ЭВМ в настоящее время - наиболее универсальный и эффективный метод оценки характеристик сложных систем. Наиболее ответственными и наименее формализованными моментами в этой работе являются проведение границы между системой 5 и внешней средой Е, упрощение описания системы и построение сначала концептуальной, а затем формальной модели системы. Модель должна быть адекватной, иначе невозможно получить положительные результаты моделирования, так как исследование процесса на неадекватной модели вообще теряет смысл. Под адекватной моделью будем понимать модель, которая с определенной степенью приближения на уровне понимания моделируемой системы S разработчиком модели отражает процесс ее функционирования во внешней среде Е. [c.82]
Вопросы оценки адекватности традиционно считаются и являются актуальными, сложными и довольно далекими от разрешения. Выделяются два способа оценки адекватности математических моделей и алгоритмов. [c.112]
Вычислительные эксперименты по оценке адекватности математических моделей и алгоритмов подразумевают их планирование, ориентирующееся на обеспечение наиболее точной или приемлемой оценки уровня адекватности при условии минимизации затрат на исследование этой адекватности или невыхода уровня таких затрат за установленное заранее значение. [c.113]
Таким образом, эксперимент по оценке адекватности математической модели или алгоритма допускает интерпретацию как планирование эксперимента с векторным откликом и смешанным характером факторов (часть из них — количественные, а часть — качественные). Поэтому правомерно применение традиционных методов планирования экспериментов, дополненных неформальной корректировкой. [c.113]
Статистический анализ имеющихся данных о ценах, объемах продаж товаров и оценки их соотношения либо за определенный период времени, либо в различных регионах за определенные периоды времени. Построение адекватной модели и анализ данных с помощью соответствующих статистических методов требует достаточной квалификации. [c.470]
Третья глава — Способы принятия решений при имитационном моделировании многоуровневых систем и объектов , позволяет формировать подходы к имитационному моделированию многоуровневых систем. Она раскрывает важное понятие межуровневой координации через оценку отношений порядка , существующих между элементами моделируемого объекта. Дело в том, что каждый элемент объекта при взаимодействии с другими обладает определенным отношением порядка , которое выражается либо степенью его важности или значимости, либо первоочередности, либо каким-то другим преимуществом или подчиненностью. Учитывать это можно только при построении имитационных моделей, а не учет этих свойств элементов моделируемого объекта не позволит построить адекватную модель. Особенно важно учитывать отношения порядка при моделировании принятия решений, где каждый элемент дерева решений , влияющий на принятие конкретного решения обладает различным отношением порядка . Правильное установление отношений порядка важно иметь и при моделировании конкретных экономических объектов — предприятий, банков, транспортных систем и т.п., так как это влияет на очередность и координаты следования моделируемых сигналов или воздействий, а от этого зависят последо- [c.9]
Учитывая сказанное, теперь можно приступить к оценке адекватности полученной модели, для чего исследуется компонента Е,. Оценка адекватности осуществляется путем исследования трех условий применительно к ряду Е,. Это условия случайности, нормальности и независимости компоненты Е,. [c.61]
При исследовании параметрических моделей регрессии наиболее распространенным типом оптимизируемого (с целью нахождения оценок неизвестных значений параметров регрессии) критерия адекватности модели является взвешенный (или обобщенный) критерий наименьших квадратов (см. (9.1), (9.2)). Следует стремиться к построению таких вычислительных алгоритмов решения оптимизационных задач, которые [c.318]
На этом этапе определяются, какие из переменных являются случайными, какие детерминированными. После определения структуры модели производится оценка значений ее параметров, чему предшествует этап сбора необходимой исходной информации. Данный этап должен обязательно закончиться проверкой адекватности модели объекту. Общей методики проверки адекватности не существует. Модель считается адекватной объекту исследования при наличии утвердительных ответов на ряд вопросов [c.193]
Следовательно, в отношении таких моделей незачем отвечать на вопросы об их научной обоснованности и точности. Второй класс моделей — это те модели, которые менее строго, формально обоснованы, однако ЛПР имело возможность не раз убедиться в полезности использования на практике результатов моделирования на них. В любом случае ясно, что только практика может ответить на вопрос, адекватна модель или нет. Следовательно, если оценка фактической эффективности, полученная после проведения операции (см. п. 1.1.3), показывает, что использование результатов моделирования оказалось полезным, то рекомендуем ЛПР считать такую модель адекватной целям и задачам моделирования и больше не терзаться вопросами "теоретической обоснованности и точности". Лучше уделить больше внимания вопросам представления информации по результатам моделирования. В этой задаче большую пользу может оказать изучение эффективных технологий и приемов, изложенных в специальной литературе [3]. [c.139]
Итогом работ по выбору вида математической модели прогноза является формирование ее обобщенных характеристик. В обобщенную характеристику должны быть включены вид уравнения регрессии, значения его параметров, оценки точности и адекватности модели и сами прогнозные оценки, точечные и интервальные. [c.185]
Для этого могут быть использованы проверки трех видов. При проверке первого вида следует проверить не будет ли модель давать просто абсурдные ответы. Второй метод оценки адекватности модели называется верификацией. Верификация имитационной модели -проверка соответствия ее поведения предположениям экспериментатора. Это первый этап действительной подготовки к имитационному эксперименту. Подбираются некоторые исходные данные, для которых могут быть представлены результаты просчета. Если окажется, что ЭВМ выдает данные, противоречащие тем, которые ожидались при формировании модели, значит, модель неверна. В обратном случае переходят к следующему этапу проверки работоспособности модели - ее валидации. [c.30]
Регулярная оценка адекватности модели путем тестирования по историче ким данным (ba fetesting) представляет собой наиболее известный способ вер фикации VaR-моделей, получивший официальный статус с принятием стран ми Группы 10 подхода на основе внутренних моделей. Стандартная метода Базельского комитета предусматривает, что банки, использующие VaR-моде для расчета размера резервируемого капитала, обязаны ежеквартально пров дить тестирование моделей по историческим данным для оценки ее адеква ности, основанное на сравнении дневной прогнозной величины VaR с факт ческими изменениями стоимости портфеля для каждого дня за последние 2i дней торгов [79]. В зависимости от количества превышений убытками велич ны VaR орган надзора может увеличивать требования к достаточности капит ла, что фактически является формой калибровки моделей, занижающих риск Существуют и более сложные методы верификации, такие как критерии согл сия А -квадрат и Колмогорова-Смирнова (проверка реального распределения д ходностей на соответствие нормальному закону), критерий Купера, провер на независимость случаев превышения убытками величины VaR и др. [c.610]
Важным элементом анализа является оценка адекватности модели. Для этого необходимо проанализировать критерий Фишера-Снедекора (F), который также представлен в диалоговом окне на рисунке 3.8. В нашем примере F(5,24) = 117,36. Расчетное значение FP необходимо сравнить с табличным, которое при данных степенях свободы 5 v =5 и V2 = 24 будет равно FT = 2,62. [c.105]
При этом формирование адекватных моделей оценок деятельности менеджеров приобретает особую важность. Оценка менеджера должна основываться на следующих четырех принципах2 [c.466]
Второй способ. В принципе возможна вариация предложенной процедуры, которая применяется хотя и реже, чем указанная, но тоже достаточно распространена при проведении научных исследований. Речь идет о важном классе проверочных экспериментов, в которых реальный объект заменяется сертифицированной, эталонной моделью. Как правило, такая пробирная модель является более подробной, чем проверяемая на адекватность, и применимой для более широкого множества допустимых вариантов. Преимущества рассматриваемого метода очевидны уменьшение затрат, в том числе временных, на оценку адекватности за счет отказа от обследования реального объекта, более представительные испытания для несравненно более широкого спектра ситуаций. Недостатки также просматриваются довольно явственно внесение дополнительных погрешностей, присущих идеальной модели, необходимость полномасштаб- [c.112]
Сформулированные с помощью содержательного и геометрического анализа рабочие гипотезы об общем виде искомой функции регрессии могут быть проверены с привлечением соответствующих матгматико-статистических критериев. Среди фундаментальных идей, на которых базируются эти статистические критерии, следует выделить а) идею компромисса между сложностью регрессионной модели ( емкостью класса допустимых решений) и точностью ее оценивания б) идею поиска модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается в) идею проверки гипотез об общем виде функции регрессии на базе сравнения выборочных критериев адекватности и исследования статистических свойств получаемых при этом оценок размерности модели. [c.207]
ХФ (к — л) + дН (х — fi), где Ф — функция нормального распределения, а Я — функция распределения произвольного симметричного относительно нуля закона не очень подходит как из-за симметрии Я, так и из-за того, что асимптотика, в которой q и Я фиксированы, а объемы выборки п -> оо, не вполне адекватна статистической практике с ростом объема выборки мы узнаем FQ с возрастающей точностью и в принципе могли бы путем преобразования переменных усилить близость распределения к нормальному закону. Более адекватной моделью засорения является схема последовательности серий выборок растущего объема, в которой пропорция засорения q= yn 1/2 убывает с ростом п [149, 215 и 14, п. 6.1.11]. 7.2.4. Эв-регрессия (i-регрессия). Ниже, используя тот же методический прием, что и при введении эв-оценок [14, п. 10.4.6],. с помощью цепочки определений вводится эв-регрессия и специальная мера отклонения от нее. Далее показывается, что эв-регрессия обладает рядом свойств, похожих на свойства обычной мнк-регрессии. Это облегчает содержательную интерпретацию эв-регрессии и выбор подходящего для конкретного случая значения Я. В заключение приводится асимптотическое разложение для оценок параметров эв-регрессии. [c.218]
Значение критерия Фишера, вычисленное по формуле (10.10) сравнивают с табличным значением для выбранного уровня значимости. Если расчетное значение не превышает табличного, то гипотезу адекватности принимают. Для отыскания табличного значения критерия требуется еще знать число степеней свободы, связанных с числителем и знаменателем выражения (10.10). Они представляют собой знаменатели тех формул, по которым вычисляют соответствующие дисперсии. Наряду с прямой оценкой адекватности, которая описана выше, существует ряд косвенных признаков, по которым можно судить о степени адекватности модели. Часто для оценки дисперсии опыта используют параллельные эксперименты в нулевой точке. Различие между средним значением из этих опытов и свободным членом линейного уравнения характеризует суммарный вклад квадратичных эффектов. Если это различие незначимо, например по критерию Стьюден-та, то можно предполагать, что модель адекватна. Такая проверка не является абсолютной, так как возможно, что сумма положительных коэффициентов при квадратах близка к сумме отрицательных. [c.231]
Смотреть страницы где упоминается термин Оценка адекватности модели
: [c.84] [c.69] [c.213] [c.153] [c.290] [c.93] [c.18] [c.18]Смотреть главы в:
Имитационное моделирование экономических процессов -> Оценка адекватности модели
