Необходимым условием максимума функции и(у) в точке у при выполнении ограничений задачи (6.9) является существование такого множителя Лагранжа К, что при у = у и К — Я выполняются условия [c.119]
Как можно проверить, стационарная точка функции Лагранжа в данном случае соответствует минимуму X. Поэтому оптимальное распределение ресурсов и плановые задания, соответствующие этому распределению ресурсов, имеют вид [c.340]
Множитель Лагранжа в задаче (1.2) — (1.4) согласно его интерпретации, приведенной в 4 гл. 1, равен отношению прироста затрат к приросту выпуска на эффективной кривой, т. е. угол наклона касательной к эффективной кривой в точке (X, У , который мы обозначим через а, связан с множителем Лагранжа [c.343]
Коэффициент k называется множителем Лагранжа. Если в исходной задаче имеется набор ограничений, то в альтернативной задаче во втором слагаемом появляется сумма слагаемых с коэффициентами k(i). Если ограничения по г-му ресурсу в точке экстремума обращаются в равенство, то множитель Лагранжа для них не равен нулю. Если ограничения в точке экстремума не оказывают влияние на решение, то множитель Лагранжа для них равен нулю. [c.120]
В этом случае решение, как правило, оказывается в точке стационарности функции Лагранжа задачи (5.47), (5.53). [c.186]
Если Р (х) — искомое решение, то найдется такой ненулевой вектор множителей Лагранжа А = (До,. ..Дт), что в точках xv функция [c.319]
Достигает ли функция Лагранжа максимума в точке ж Условие (9.79) теоремы Куна-Таккера совпадает по форме с необходимым условием максимума функции Лагранжа R на множестве Vx. В связи с этим возникает желание заменить условие (9.79) условием [c.335]
Так как производные в (9.241) представляют собой не что иное, как значения множителей Лагранжа А в задачах 1 и 2 соответственно, то из (9.241) следует, что векторы множителей Лагранжа в этих задачах, а следовательно, и в выражениях (9.229) и (9.230), равны друг другу. [c.392]
Пользуясь методом множителей Лагранжа, показать, что минимум достигается в точке (0,0) при А = 1. Рассмотреть функцию Лагранжа [c.183]
Таким образом, множитель Лагранжа AQJ показывает, как меняется значение целевой функции в точке оптимума при малых изменениях в правой части j-ro ограничения. Предположим, например, что мы максимизируем прибыль фирмы при условиях ограничений на ресурсы. Тогда множитель Лагранжа АО — это дополнительная прибыль, которую фирма могла бы заработать при увеличении запаса данного ресурса на единицу, что, по сути, является максимальной ценой, которую фирма готова платить за эту дополнительную единицу ресурса. По этой причине множитель АО часто называется теневой ценой 1. [c.192]
Для выяснения геометрического смысла теоремы Лагранжа заметим, что левая часть (8АЛ) есть угловой коэффициент секущей, проходящей через точки А (а, /(а)) и В ( ,/( )) кривой у = f(x), a правая часть есть угловой коэффициент касательной к той же кривой в точке С ( , /(О)- Теорема Лагранжа о среднем значении функции утверждает, что на кривой у = f(x) между точками А я В всегда найдется такая точка С, касательная к которой параллельна секущей АВ (рис. 8А.1). [c.344]
Для того чтобы осуществить стандартное исключение вариации Ъх, нужно в тождестве Лагранжа ликвидировать лишнее слагаемое ф8а +s. Это приведет к разрыву функции ф (t) в точке t с опре- [c.70]
Теорема. Пусть в точке х, удовлетворяющей связям f (х)=0, i—i,. . ., т, градиенты f x (х), i=0, 1,. . ., ттг, — линейно независимы (т. е. множителей Лагранжа, удовлетворяющих (22). не существует). Тогда в окрестности х может быть найдена точка ж+ Ъх, удовлетворяющая связям и условию /° (х+ а ) < /° (х). [c.399]
Здесь мы предположим, что налог v является величиной постоянной, неизменной и полностью предсказуемой. Поскольку непредвиденный налог даст непредвиденный результат, вряд ли нам удастся выстроить общую теорию для подобных налогов. Однако любой налог, сумма которого изменяется со временем, определенным заранее установленным образом, даст предсказуемые результаты. В связи с этим интересной задачей является выбор шкалы налоговых ставок v, которая может включать такие значения темпа производства, q, и совокупной добычи, х, а также времени, чтобы, когда монополист выберет график производства, обеспечивающий максимизацию его прибыли, общественная ценность U была больше, чем при любой другой принятой налоговой ставке. Это приводит нас к решению задачи типа задачи Лагранжа в расчетах вариаций, где точка на одном конце переменна. Примем q = dx/dt и [c.296]
Подставляя в (3.9) х вместо 5 и освобождаясь от множителя Лагранжа, получаем, что равенство спроса и предложения возможно, если цены пропорциональны предельным полезностям в точке S = х [c.53]
Прежде всего выясним, в какой степени множители Лагранжа в этих задачах выполняют функции цен. О функциях цен в социалистической экономике в ранее упомянутом сборнике сказано следующее В экономической литературе, посвященной проблемам планового ценообразования, пока еще нет единства в определении числа функций цены при социализме и в характере самих функций. Но наиболее часто называются следующие основные функции планово-учетная, стимулирующая и распределительная 2. В соответствии с планово-учетной функцией цены должны отражать общественно необходимые затраты труда 3. Как бы ни определялись общественно необходимые затраты труда, ясно, что множители Лагранжа в задачах (3.11), (3.19) не могут выполнять планово-учетную функцию цен на ресурсы, так как ресурсы в этих задачах уже имеются в наличии и затраты труда на их производство в модель не включены более того, если речь идет о природных или трудовых ресурсах, то и проблема учета общественно необходимых затрат труда на их производство не возникает. Отпадает и стимулирующая функция, так как модели типа (3.11), (3.19) не содержат описания механизма стимулирования. Остается распределительная функция. Рассмотрим ее подробнее. [c.59]
Функция (10.4) называется функцией Лагранжа, а числа — множителями Лагранжа. Если функция (10.2) в точке х° = (хД х2°,. .., лс °) [c.350]
Найдем вариацию функционала %. Пусть ( ") - стационарная точка fi, а х (1-а, е) — близкие сравниваемые законы движения. Поверхность разрыва у закона движения ( ", б) обозначим через 2С. Как при выводе уравнений Лагранжа в 2 гл. I, удобно ввести отображение V - V % " = = "( , б), при котором поверхность 2 переходит в поверхность 2е. В силу близости 2 и 2е можно написать " = " +5 ", где 5 " - гладкие функции в V. Функции 5 " обращаются в нуль на 8F, поскольку граница области V неподвижна по частицам. [c.181]
Функцию Лагранжа в этой задаче можно интерпретировать как ценностное выражение результата производства, состоящего в получении дохода и сохранении неиспользованных ресурсов, а множители Лагранжа являются здесь оценками единицы неиспользованных ресурсов разных видов. Экономический смысл седловой точки у функции Лагранжа состоит в том, что между оценками, ценами имеющихся ресурсов и величиной дохода имеется равновесие, отклоняться от которого не выгодно ни при управлении производственным процессом, ни при назначении цены на ресурсы. [c.107]
Достаточно легко проверить, что задачи (6.16)-(6.17) и (6.18)-(6.19) образуют двойственную пару. Здесь в определенном смысле мы вернулись к проблемам, уже рассматривавшимся во второй главе, а именно к взаимосвязи между наличием решения у некоторой оптимизационной задачи и существованием седловой точки у соответствующей функции Лагранжа. В данном случае аналогичная связь прослеживается между седловой точкой игры и решением пары задач оптимизации. [c.194]
Функция Лагранжа для соответствующей задачи (13) равна L = pyj + / / (%), где Hj — множитель Лагранжа для технологического ограничения. При условии р О в точке максимума yj выполняется dL(yj)/dyk = О, откуда pk = fk(yj)nj (Vf G К) (здесь и далее fk — производная по товару k в точке y j). Рассматривая товары с ненулевыми ценами, заметим что //,, = О, и исключив //,,, получим дифференциальную характеристику точки равновесия производителя y j. [c.14]
Таким образом, дифференциальные характеристики оптимума и равновесия совпадают, что позволяет подобрать оценки Л, //, а Лагранжиана (49) такие, что в точке (х, у) Лагранжиан достигает безусловного экстремума, то есть выполнено необходимое условие условного экстремума задачи (52). Благодаря выпуклости этой задачи необходимое условие совпадает с достаточным, таким образом равновесие (х, у) является также решением задачи (52), что и требовалось для Парето-оптимальности. [c.34]
По теореме Джона найдутся множители Лагранжа Хг > 0 (г е /), ц 0 (j e J) и af (k
Так называемые условия первого порядка — условия, необходимые для того, чтобы функция U. (Q) имела максимум или минимум в точке (Р. Эти условия дают критические точки функции Лагранжа LUi (Q, Л) из равенства grad Lv< = 0. Однако из этих условий не следует, какой именно является критическая точка — максимумом или минимумом функции U. (Q). Уточнением сформулированной позиции является следующая запись [c.228]
При этом одно из базовых значений Т соответствует предельно возможной температуре рабочего тела Т = Ттах, а второе вместе с множителем Л находится из условия стационарности по Т функции Лагранжа L и равенства значения L в точке стационарности значению в точке Т [c.75]
Если оптимальное решение х лежит на границе Vx, например, неотрицательная составляющая xv вектра х в точке х равна нулю, то по этой составляющей допустимы только неотрицательные вариации 6х > 0, приращение целевой функции, а значит, и функции Лагранжа на этих вариациях должно быть неположительно. Условия оптимальности в этом случае можно переписать в форме [c.334]
Если х — решение задачи (9.65), то найдется такой вектор множителей Лагранжа А с составляющими Ao,Ai,A2,... (До равно нулю или единице] все составляющие вектора Д не равны нулю одновременно), что в точке х выполнены условия (9.79) и условия дополняющей нежесткости. [c.335]
Таким образом, если решение х задачи (9.89) невырожденное (До = 1), то антиградиент функции достижимости в точке С° равен вектору множителей Лагранжа А задачи (9.89) при d = f. В частности, при f = 0 в невырожденной задаче НП (До = 1) множители Лагранжа характеризуют чувствительность значения задачи к изменению ограничений. Если некоторое ограничение несущественно и его малое изменение никак не повлияет на значение целевой функции в точке х, то соответствующий множитель Лагранжа равен нулю. [c.340]
| Рис. 9.9. Функции достижимости, для которых расширение Лагранжа эквивалентно a — недифференцируемая в точке С = 0 б— дифференцируемая в точке С = О | 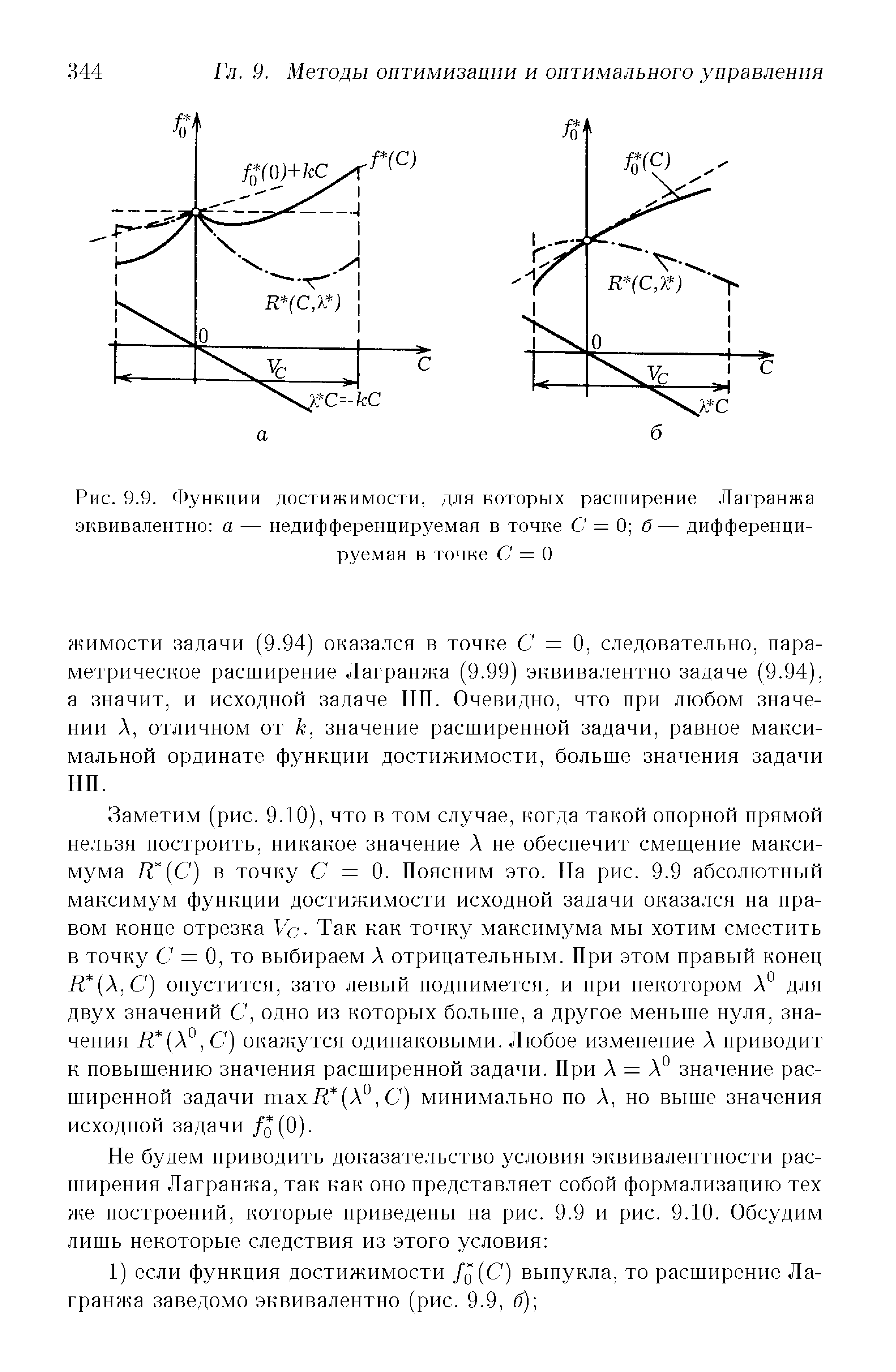 |
Величина т0 с1 + V(q) есть энергия покоя материальной точки. Таким образом, действие представляет сумму по всем моментам собственного времени величины, имеющей ясный физический смысл полной энергии покоя точки. "Странное" выражение для функции Лагранжа в виде разности кинетической и потенциальной энергии представляет ньютонианский предел плотности действия, отнесенного к единице времени наблюдателя. [c.25]
Х< А справедливо неравенство d2f/dx2>0. Рассмотрим минимум строго выпуклой функции f(A i) + f(A 2) + f(A 3) при ограничении A i + А2 + + Аз - onst = с. Вводя множитель Лагранжа, убеждаемся, что минимум достигается npn li =A2 =А3. Следовательно, в точке минимума [c.248]
Критическая точка (x.0(Q,x,0(Q,A,°(Q) функции Лагранжа, удовлетворяющая системе (12) и взятая без последней координаты (множителя Лагранжа) X°(Q, т.е. точка (xta(Q,x2u( )), и есть решение задачи (7), ( 1 1 ) максимизации выпуска при данных фиксированных издержках производства С. Подставив точку (х,°(С),(.х20(С)Л0(О) в первые два уравнения системы (12), получим два тождества. Поделив почленно первое тождество на второе, получим, очевидно, выражение (3) (множитель Лагранжа Х°( С) сократится). Получили аналитическое обоснование того, что в точке (х,°(С),х20(С)) изокванта и изокоста касаются (см. рис. 1 1.6). Вообще говоря, критическая точка функции Лагранжа, взятая без последней координаты, не обязана быть решением задачи (7), (1 1) на условный максимум. В случае же производственной функции Л, ,, ), удовлетворяющей определенным требованиям гладкости и выпуклости, критическая точка функции Лагранжа (без последней координаты) есть решение задачи (7), (11) на условный экстремум. Отметим также, что в случае производственной функции Л, , ) х,°(С)>0, x2°( )>0, Х°(С)>0. [c.189]
В разделе 2 в точке локального рыночного равновесия (х,°,х2°) был определён объём производства .ДхДх,0). Если в ограничении (17) положить у=у0, то несложно показать, что х,°(> 0)=х10) х2°(у0)=х2°, а также К°(у0)=р0, т.е. множитель Лагранжа А.0 ,,) равен рыночной цене/ 0 единицы выпускаемой продукции. Таким образом, предложена естественная экономическая интерпретация множителя Лагранжа х°о>0). [c.193]
Если (х, и) — седловая точка функции Лагранжа, в области лге зэД и>0,то х является оптимальным планом задачи (2.28), причем справедливо так называемое правило дополняющей нежесткости [c.103]
