Модели скользящего среднего (МА) представляют стационарный процесс в виде линейной комбинации последовательных значений белого шума . Такие модели оказываются полезными как в качестве самостоятельных описаний стационарных процессов, так и в качестве дополнения к моделям авторегрессии для более детального описания шумовой составляющей. [c.105]
Другой механизм образования автокорреляции следующий. Случайные возмущения представляют собой белый шум ,, но на результат наблюдения у, влияет не только величина ,, но (хотя обычно и в меньшей степени) несколько предыдущих величин 5/-1,..., t-P. [c.178]
В обоих случаях , — независимые, одинаково распределенные случайные величины с нулевыми математическими ожиданиями и дисперсиями а2 (белый шум). [c.200]
| Рис. 16. Гауссовский белый шум со стандартным отклонением 1%, сконструированный с использованием генератора случайных чисел. Нарастающая сумма этих чисел определяет случайные блуждания, как сказано в тексте (см. Рис. 19). | 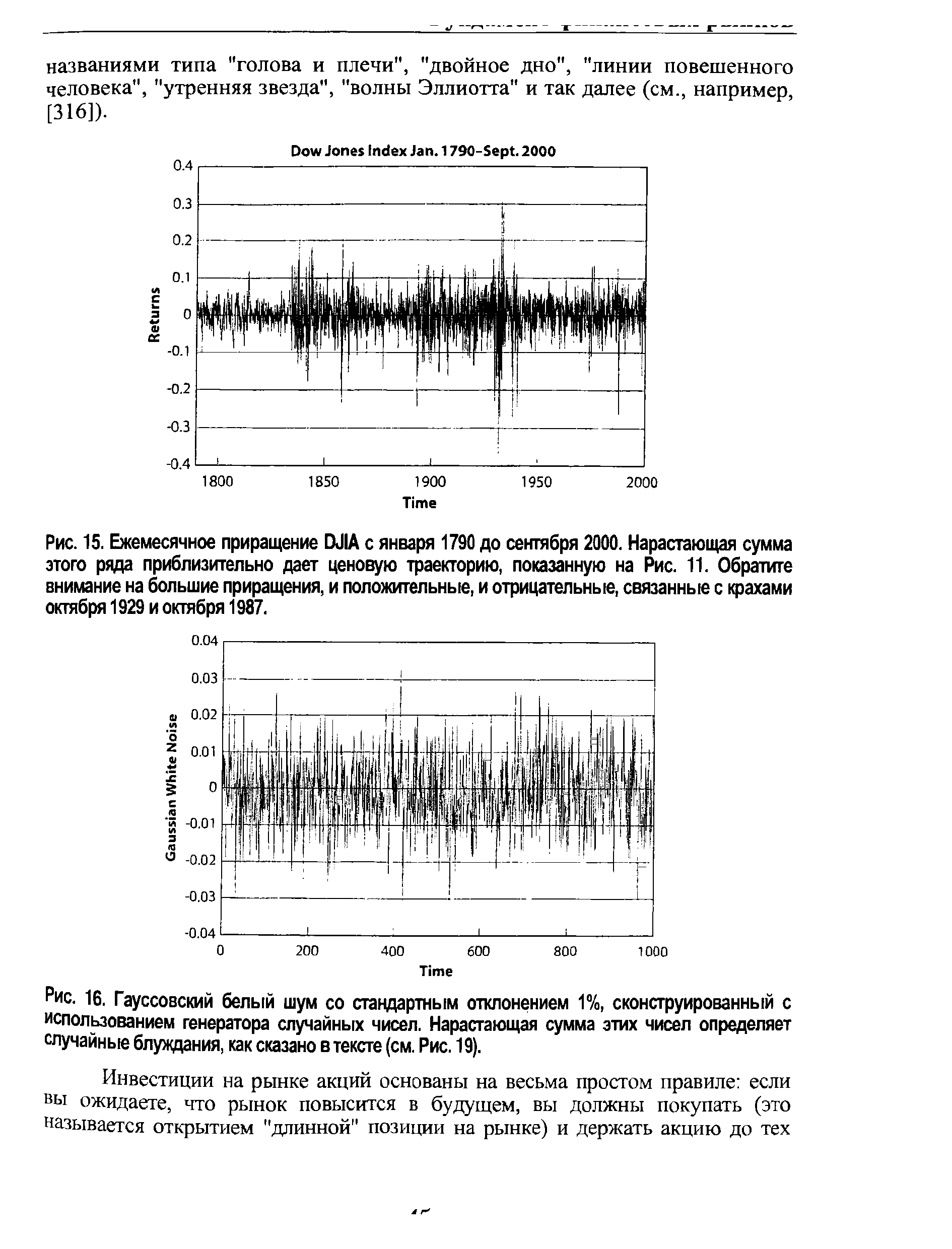 |
Непредсказуемость означала бы, что координаты точек временного ряда, соответствующие компонентам задержки, образуют случайное распределение вокруг гиперплоскости r(t = 0, т.е. белый шум. Если же распределение не является случайным, то при помощи нейронной сети можно аппроксимировать среднюю поверхность, отклоняющуюся от гиперплоскости r(t) = 0. [c.213]
Здесь st - белый шум 1, а р может принимать различные значения. [c.91]
Временные ряды называются "белым шумом", если лежащая в их основе переменная имеет среднюю, равную нулю, [c.91]
Следует также учитывать звуковые воздействия. Исследования показали, что покупатели воспринимают магазины, в которых полностью отсутствуют звуки, как отпугивающие. В таких случаях может применяться "белый шум" неясное гудение, как при работе холодильника, которое еле различимо, но все же скрадывает неприятную тишину. [c.80]
Нужно сделать еще одно важное замечание. В модели устойчивого процесса, по В. Шухарту, предполагается, что вариации параметров каждого изделия на выходе производственного процесса представляют собой последовательность случайных, независимых величин. В теории случайных процессов, в радиотехнике и радиофизике такой процесс называется белым шумом. [c.347]
Если предположение независимости случайных отклонений соседних измерений параметров процесса неверно, т. е. случайный процесс не является белым шумом, то это означает, что методами введения обратной связи, т. е. корректировки регулировок процесса по данным измерения процесса на выходе можно улучшить управление и практически устранить зависимость соседних измерений на выходе процесса. [c.347]
В теории случайных процессов количественной мерой зависимости последовательности случайных величин является коэффициент автокорреляции [170]. Этот коэффициент принимает значения от 0 до 1. При значениях коэффициента автокорреляции, близких для соседних наблюдений к 0 (на практике меньших 0,2—0,3), считается, что процесс является белым шумом. Если же значения коэффициента автокорреляции близки к 1, то для данного процесса следует использовать различные системы регулирования с обратной связью. [c.347]
В дальнейшем используются следующие обозначения Xt, xt, Zt, ztr q, v — зависимая и независимая переменные при отсутствии и наличии ошибок измерения, ошибки измерения в этих переменных и 1 ы<2> d2> — остаточные возмущения и белый шум в уравнениях для временных рядов и для временных рядов перекрестных выборок М, s2, л(1>, я(2), 2W, 2(2) — математическое ожидание, выборочная дисперсия, остаточные ковариационные матрицы и ковариационные матрицы коэффициентов в уравнениях для временных рядов и временных рядов перекрестных выборок N(0, s2), гг, Т, п, К, Е, i, ML — обозначение нормального распределения, коэффициент остаточной марковской автокорреляции первого порядка, количество наблюдений временного ряда и выборочного обследования, число независимых переменных, единичная матрица и единичный вектор, обозначение оценки наибольшего правдоподобия. [c.73]
Сигнал, спектральная плотность которого — дробно-рациональная функция частоты, можно представить как реакцию линейной системы на белый шум. Другими словами, такой сигнал может быть получен как решение линейного стохастического дифференциального уравнения, возмущаемого белым шумом. Случайный процесс — решение соответствующих стохастических дифференциальных уравнений — представляет собой марковский процесс или проекцию марковского процесса. Статистические характеристики марковских процессов — переходные вероятности — удовлетворяют известным дифференциальным уравнениям в частных производных А. Н. Колмогорова. Для вычисления условного математического ожидания М[т (0] гауссовского марковского процесса можно получить обыкновенное дифференциальное уравнение. Таким образом, выражение (4.8) для решения задачи (4.1) позволяет свести вычисление характеристик оптимальной в смысле задачи (4.1) фильтра- [c.315]
Процесс (/) представляет собой белый шум, т. е. случайный процесс, корреляционная функция которого — дельта-функция Дирака. Напомним, что все предшествующие утверждения главы относились к случайным процессам с непрерывными корреляционными функциями. [c.322]
Фильтр с функцией веса W(U, т) преобразует случайные процессы, возникающие на входе системы прогнозирования, в дополнительное искусственное рассеивание. Конструктивно может оказаться удобнее использовать в качестве источников искусственного рассеивания генераторы белого шума. [c.340]
Приведем соответствующее утверждение для многомерного случая. Пусть требуется найти корень я = 6 системы уравнений f(x)=a, где составляющие вектора f(x) наблюдаются со случайной ошибкой типа белого шума . Многомерный процесс типа (8.1) может интерпретироваться системой стохастических уравнений Ито [c.377]
Предполагалось, что рынки "эффективны" то есть цены уже отражали всю текущую информацию, которая могла предвосхитить будущие события. Поэтому мог быть смоделирован только спекулятивный, стохастический компонент изменение цен, вызванное изменениями стоимости, не могло быть смоделировано. Если рыночные прибыли являются нормально распределенным "белым" шумом, то они одинаковы на всех инвестиционных горизонтах. Это эквивалентно "шипению" магнитофона. Звук одинаков независимо от скорости магнитофонной ленты. [c.30]
Если процесс представляет собой гауссовы случайные блуждания, первые две точки не сохранятся. Белый шум кажется одинаковым на всех частотах (подобно "шипению", которое мы слышим на магнитофонных лентах и которое звучит одинаково на всех скоростях). И, кроме того, нет никаких циклов. Если разрыв графика R/S появляется в однодневном, а не в десятидневном интервале, разрыв в дневном графике был артефактом, а не истинным циклом. [c.112]
Простейшим примером стационарного временного ряда, у которого математическое ожидание равно нулю, а ошибки е/ некорре-лированы, является белый шум . Следовательно, можно сказать, что возмущения (ошибки) е, в классической линейной регрессионной модели образуют белый шум, а в случае их нормального распределения — нормальный (гауссовский) белый шум. [c.136]
Идентификацией временного ряда мы будем называть построение для ряда остатков адекватной ARMA-модели, т. е. такой А/Ш4-модели, в которой остатки представляют собой белый шум, а все регрессоры значимы. Такое представление, как правило, не единственное, например, один и тот же ряд может быть идентифицирован и с помощью А/ -модели, и с помощью М4-модели. В этом случае выбирается наиболее простая модель. [c.179]
Легко провфить, что среднее E(Sp(t)), а также двухточечная корреляция E(Sp(t),Sp(t )) для t Ф t равна нулю и, таким образом, фф также является белым шумом. Интуитивно, такой вывод возникает из того факта, что в эту характеристику временного ряда вводится нечетное число бросков монеты, чье среднее равняется нулю ((1/2) х (+1) + (1/2) х (-1) = 0). Однако, трёхточечная корреляционная функция E(Sp(t - 2) 8p(t - 1) Sp(t)) не равна нулю, но равна 1 и ожидание величины Sp(t), требующее знания двух предыдущих приращений ф - 2) и Sp(t -1) не равно нулю, а равно E(Sp(t) Sp(t -2), Sp(t -l))=ep(t - 2)Sp(t -1). Это означает, что возможно предсказать изменение цены сегодня с большей, чем 50% вероятностью, если знать изменение цены вчфа и позавчера [c.65]
Вернемся теперь к первому варианту системы с квадратичной обратной связью (см. рис. 3.2) с параметрами с0 = 0.5, с, = -0.7, с2 = 1.2, но теперь добавим к ней белый шум. Предположим, что изменения цены наполовину зависят от неинформированных инвесторов, которые реагируют на текущую цену в соответствии с приведенным выше соотношением, а на другую половину — от реакции информированных инвесторов на поступающую информацию о рынке, которая носит случайный характер. В пашей модели эта вторая составляющая цены бралась из нормального распределения5 с нулевым средним и стандартным отклонением 0.2. Результирующий доход есть среднее арифметическое от случайного дохода и дохода, определяемого обратной связью. [c.83]
Для того чтобы ошибочно не принять раньше времени локальный минимум погрешности обобщения за глобальный, наш алгоритм брал вдвое большее число эпох по сравнению с тем, на котором достигалось наилучшее обобщение. Таким образом, на самом деле, число эпох было вдвое больше, чем показано в табл. 6.3 и на рис. 6.1. При любом выборе коэффициента обучения ошибка RMSE на тестовом множестве оказывалась меньше, чем на обучающем. Этот в некоторой степени удивительный эффект может объясняться наличием белого шума в обучающем множестве и его отсутствием в тестовом множестве. Поскольку обучение прекращалось, как только RMSE на тестовом множестве начинала расти, мы полагаем, что переобучение не имело места, и что сеть не запоминала шум. Таким образом, относительно большая погрешность на обучающем множестве объясняется именно белым шумом. [c.140]
Замечание о том, что статистически устойчивый процесс должен быть белым шумом, очень важно для российских предприятий, так как исследования их процессов показывают частое наличие зависимых вариаций, а также присутствие различных временньгх трендов. [c.348]
В [212] построен непрерывный многомерный аналог процедуры стохастической аппроксимации Кифера — Вольфовица для вычисления экстремума функции регрессии. При этом предполагается, что ошибка наблюдения в момент времени t скалярной функции f(x) равна
Смотреть страницы где упоминается термин Белый шум
: [c.182] [c.219] [c.220] [c.287] [c.299] [c.64] [c.65] [c.137] [c.249] [c.88] [c.88] [c.93] [c.129] [c.287] [c.353] [c.358] [c.467] [c.471] [c.502] [c.533] [c.549] [c.97] [c.316] [c.37] [c.82]Смотреть главы в:
Основы стохастической финансовой математики Т.1 (0) -- [ c.148 , c.284 ]
Основы стохастической финансовой математики Т.2 (1998) -- [ c.148 , c.284 ]
Эконометрика начальный курс (2004) -- [ c.277 ]
Эконометрика (2002) -- [ c.16 ]
