| Рис. 16. Гауссовский белый шум со стандартным отклонением 1%, сконструированный с использованием генератора случайных чисел. Нарастающая сумма этих чисел определяет случайные блуждания, как сказано в тексте (см. Рис. 19). | 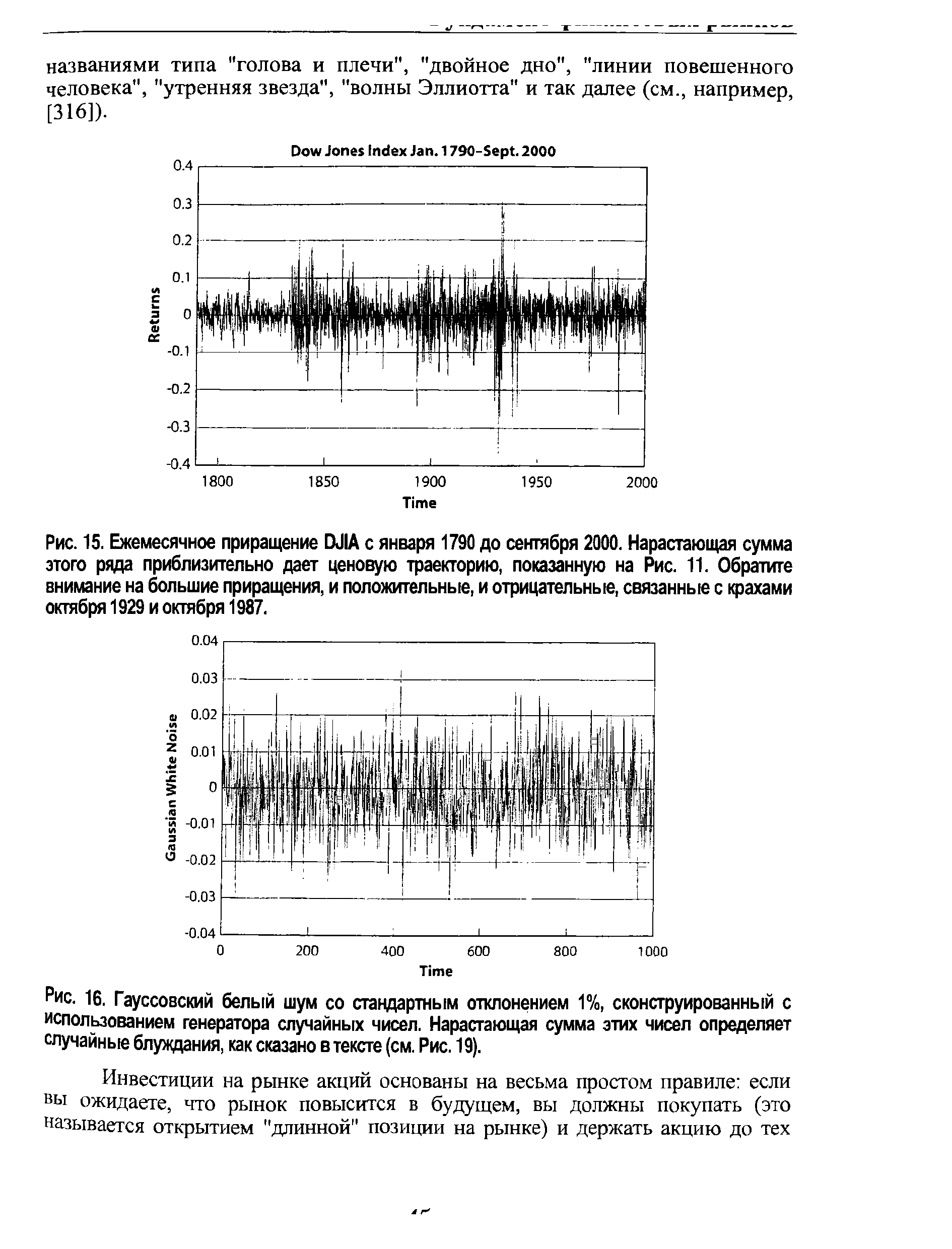 |
Сигнал, спектральная плотность которого — дробно-рациональная функция частоты, можно представить как реакцию линейной системы на белый шум. Другими словами, такой сигнал может быть получен как решение линейного стохастического дифференциального уравнения, возмущаемого белым шумом. Случайный процесс — решение соответствующих стохастических дифференциальных уравнений — представляет собой марковский процесс или проекцию марковского процесса. Статистические характеристики марковских процессов — переходные вероятности — удовлетворяют известным дифференциальным уравнениям в частных производных А. Н. Колмогорова. Для вычисления условного математического ожидания М[т (0] гауссовского марковского процесса можно получить обыкновенное дифференциальное уравнение. Таким образом, выражение (4.8) для решения задачи (4.1) позволяет свести вычисление характеристик оптимальной в смысле задачи (4.1) фильтра- [c.315]
Если Е(Е ) МО, ст2), то мы имеем дело с гауссовским белым шумом, хотя переменная белого шума необязательно должна [c.317]
Если предполагать, что белый шум в широком смысле = (е ) является гауссовским, то основным методом оценивания является метод максимального правдоподобия, согласно которому в качестве оценки параметра в (по наблюдениям h , h-z, , hn) берется значение [c.165]
При Н = j (обычное броуновское движение) величины У = (Уп) образуют гауссовский "белый шум" с p(k) = 0, k 1. Если же 0 < Н < i то [c.204]
Сравним результаты этой таблицы с теми оценками для vmj, которые получаются при моделировании гауссовского белого шума с теми же [c.225]
ТАБЛИЦА ЗЬ. Значения vm,j для гауссовского белого шума [c.226]
V(t) -векторный гауссовский случайный процесс белого шума (т. е. случайный процесс, имеющий корреляционную функцию в виде дельта-функции Дирака) с математическим ожиданием, равным нулю. [c.183]
X взаимно независимы и имеют одинаковое нормальное распределение N(0, а ), образуя случайную выборку из этого распределения, т.е. Xt i.i.d. N(Q,
Заметим, однако, что здесь наблюдается некоторая асимметрия распределения вероятностей значений xt (скошенность этого распределения в сторону положительных значений), что исключает описание модели этого ряда как гауссовского белого шума. [c.16]
В установлении пригодности модели a(L) yt = b(L) xt + et с помощью различных критериев адекватности гипотеза о том, что ряд st является гауссовским белым шумом, не должна отвергаться - в противном случае следует говорить о непригодности уже этой общей модели. [c.91]
Во всех случаях в качестве начального значения Х взято Х = О и использовалась одна и та же последовательность значений е , . .., т, имитирующая гауссовский белый шум с дисперсией, равной единице [c.99]
При a = 1 имеем tp = a - 1= 0, и приращения A Xt ряда Xt образуют процесс белого шума, так что условное математическое ожидание A Xt при фиксированном (наблюдаемом) значении Xt- = xt- не зависит от xt- и равно 0. Соответственно, при фиксированном (наблюдаемом) значении Xt- = xt- , условное математическое ожидание случайной величины Xt = AXt + Xt- равно xt- . Если распределение случайной величины st симметрично относительно нуля (а именно таково и гауссовское распределение, которое использовалось нами при моделировании), то [c.101]
Не зная точно процесс порождения данных, мы должны были бы начать с исследования отдельных рядов. У всех четырех рядов не обнаруживается детерминированного тренда. Проверка по критерию Дики - Фуллера дает значения -статистик, равные -2.18, - 1.78, - 0.57, -1.70, соответственно. Все 4 ряда признаются интегрированными. Продифференцированные ряды идентифицируются как гауссовские белые шумы, так что ряды y t, yit, yit, y4t идентифицируются как AR(1) ряды с единичным корнем, т.е. как интегрированные ряды порядка 1. [c.197]
При этом гипотеза гауссовского белого шума для ряда остатков не отвергается. Это означает, что мы имеем здесь дело со стохастической коинтеграцией. В рамках расширенной модели не отвергается гипотеза о равенстве 0.5 коэффициентов при тренде и Wt. График ряда Vt - Q.5t - 0.5 Wt имеет вид [c.219]
Здесь V дискретный m-мерный гауссовский белый шум с нулевым математическим ожиданием и единичной ковариационной матрицей. W т-мерная стационарная гауссовская последовательность, [c.36]
Предположим теперь, что входное возмущение W является случайным сигналом, априорная информация о вероятностном распределении которого исчерпывается следующим W - mi -мерная стационарная гауссовская последовательность, средняя анизотропия которой ограничена сверху известным неотрицательным параметром о. Точнее, последнее означает, что W генерируется из mi-мерного гауссовского белого шума V с нулевым математическим ожиданием и единичной ковариационной матрицей посредством неизвестного формирующего фильтра G, лежащего я семействе [c.37]
Соответствующую этому случаю последовательность Л = (Лп)> являющуюся гауссовской последовательностью независимых одинаково распределенных величин, называют, как указывалось выше, белым (гауссов-ским) шумом. [c.286]
Подчеркнем, что во всех этих моделях был один источник случайности - белый (гауссовский) шуме — ( п)- [c.348]
В модели же "стохастической волатильности" (см. п. 7 в Id, гл. II) предполагалось, что имеются два источника случайности - независимые белые (гауссовские) шумы е — (еп) и S — (Sn). При этом hn — <ТП.ЕП, где <т = е2д" с [c.348]
Простейшим примером стационарного временного ряда, у которого математическое ожидание равно нулю, а ошибки е/ некорре-лированы, является белый шум . Следовательно, можно сказать, что возмущения (ошибки) е, в классической линейной регрессионной модели образуют белый шум, а в случае их нормального распределения — нормальный (гауссовский) белый шум. [c.136]
В [212] построен непрерывный многомерный аналог процедуры стохастической аппроксимации Кифера — Вольфовица для вычисления экстремума функции регрессии. При этом предполагается, что ошибка наблюдения в момент времени t скалярной функции f(x) равна
Если в этом определении добавить еще требование гауссовости (нормальности), то получаемую последовательность е = (еп) называют белым шумом в узком смысле или белым (гауссовским) шумом, или просто белым шумом, что равносильно тому, что е = (еп) есть последовательность независимых нормально распределенных, en /К(0, сг ), случайных величин. В дальнейшем мы будем считать сг2 = 1. (В этом случае часто говорят, что е = (еп) - стандартная гауссовская последовательность полезно сравнить это понятие с фрактальные гауссовским шумом, также используемым в статистике финансовых данных см. 2d, гл. III.) [c.148]
Временной ряд, соответствующий процессу белого шума, ведет себя крайне нерегулярным образом из-за некоррелированности при t s случайных величин Xt иXs Это иллюстрирует приводимый ниже график смоделированной реализации гауссовского процесса белого шума (NOISE) с D(Xt) = 0.04. [c.15]
Имея в виду возможность идентификации моделей AR(/ ) и МА(д) по графикам функций r(k) и rpart(k), желательно иметь статистические критерии для проверки гипотез о равенстве нулю тех или иных значений p(k) и ppart(k) на основании наблюдаемых значений r(k) и rpart(k). Вопрос этот весьма сложный, и мы ограничимся только двумя приближенными рецептами, которые предполагают гауссовость инноваций (т.е., что et - гауссовский белый шум). [c.35]
В процедуре Йохансена предполагается, что et - TV-мерный гауссовский белый шум, так [c.222]
В соответствии с 2а, гл. II, такую последовательность мы называли белым (гауссовским) шумом и использовали как источник случайности при образовании разнообразных случайных процессов, как линейных (МА, AR, ARMA,. ..), так и нелинейных (AR H, GAR H,. ..). [c.284]
Если Sn = SoeHn, HO = 0, причем A.ffn = ren, n 1, где (еп) - белый гауссовский шум, п ->V(0,1), то под волатильностью понимают естественную здесь меру неопределенности и изменчивости - стандартное отклонение а. [c.414]
Если, к примеру, промоделировать величины h = (/гп)п ъ согласно (16), с белым гауссовским шумом е = ( n)n i, то мы найдем, что новые величины V° — Vn(/i°), построенные по h° = (/i )n>i > веДУт себя именно так, как это должно быть для фрактального гауссовского шума с Н = 1/2. Следующий рисунок качественно иллюстрирует описанные явления [c.447]
