Так как bi, Ь2. .. —независимые и одинаково распределенные случайные величины, то [c.81]
Практический смысл этой теоремы очень прост. Любые сложные работы на объектах экономики (ввод информации из документа в компьютер, проведение переговоров, ремонт оборудования и др.) состоят из многих коротких последовательных элементарных составляющих работ. Причем количество этих составляющих работ иногда настолько велико, что требования в приведенной выше теореме о независимости и- одинаковом распределении становятся излишними. Поэтому при оценках трудозатрат всегда справедливо предположение о том, что их продолжительность - это случайная величина, которая распределена по нормальному закону. [c.30]
В однородной модели Кокса-Росса-Рубинштейна величины ", , являются независимыми и одинаково распределенными с [c.234]
В этой модели S - цена актива без каких-либо специальных ограничений типа цены облигации с погашением (в момент погашения цена равна номиналу облигации), например, это цена акции. Пусть единица временного промежутка есть день. Тогда цена актива к концу л-го дня будет S SQ+XI +. ..+ХП, где S0 - цена в начале наблюдения, х, i=, ...,n, - независимые и одинаково распределенные случайные величины, принимающие значения —1,+1 с вероятностью 1/2. Поведение возможной цены актива изобразим на рис. 13.1 [c.103]
Математическая сложность состоит в том, что мнения экспертов лежат в некотором пространстве объектов нечисловой природы. Общая теория подобного усреднения построена в ряде работ, в частности показано, что в силу обобщения закона больших чисел среднее мнение при увеличении числа экспертов (чьи мнения независимы и одинаково распределены) приближается к некоторому пределу, который называют математическим ожиданием (случайного элемента, имеющего то же распределение, что и ответы экспертов) [58]. [c.333]
Пусть г ог, t = 1,. . . , гг — независимые и одинаково нормально распределенные векторы со средним 0 и неизвестной, положительно определенной ттг х ттг ковариационной матрицей И0. [c.415]
В дискретные моменты времени п— 1, 2,. .. наблюдаются значения y(Xn)=f(xn)+v>n. Предполагается, что а — случайная величина с нулевым математическим ожиданием и что ее значения для различных моментов времени независимы и одинаково распределены с функцией распределения, обладающей непрерывной ограниченной плотностью. [c.370]
В соответствии со структурой описанной АС, информированностью центра и порядком выбора АЭ своих действий проведем классификацию АС. Во-первых, будем различать АС с одним или несколькими (возможно, случайным числом) АЭ. Во-вторых, будем различать детерминированные АС, т.е. те, в которых состав участников и их характеристики фиксированы и известны центру, и АС с вероятностной неопределенностью, т.е. те, в которых состав участников определяется некоторым вероятностным законом. В последних будем различать АС с фиксированным и случайным набором АЭ. В АС с вероятностной неопределенностью в дальнейшем будем считать, что типы АЭ независимы и одинаково распределены по некоторому вероятностному закону распределения на fi = [r0,ri]. [c.22]
Предположим, что случайные ошибки eit независимы и одинаково распределены в обоих направлениях и имеют симметричное распределение с функцией распределения G и что объясняющие переменные строго экзогенны. [c.317]
В обоих случаях , — независимые, одинаково распределенные случайные величины с нулевыми математическими ожиданиями и дисперсиями а2 (белый шум). [c.200]
Рассмотрим сумму X+(f0,t) = x(l)(t0,t)+...+xM(t0,t) депозитов, лежащих на счетах потенциальных вкладчиков к моменту времени t. Эта. случайная величина получена с учетом возможности и того, что счета некоторых потенциальных вкладчиков не будут открыты к моменту времени t, и того, что счета ряда потенциальных вкладчиков, открытые в некоторый момент времени те [t0,t], будут ликвидированы к указанному моменту t. Предполагается, что случайные величины x(i)(t0,t), i = 1,.., s+ независимы в совокупности и имеют одинаковое распределение — распределение случайной величины x(t0,f). [c.198]
Характеристика X является случайной величиной. Если опыты (наблюдения) производились в одинаковых условиях и независимо друг от друга, то выборку (х , х2,..., хп) можно рассматривать как п-мерный случайный вектор, где величины х независимы, и каждая из них распределена так же, как и случайная величина X в генеральной совокупности. В этом случае можно сказать, что выборка (х,, х2,...,хп) взята из генеральной совокупности случайной величины Хс теоретической функцией распределения F(x). [c.37]
Наиболее распространенными являются биномиальная и гипергеометрическая модели. В биномиальной модели предполагается, что результаты контроля п единиц можно рассматривать как совокупность п независимых, одинаково распределенных случайных величин хи х2,. .., х , где х, = 1, если /-е измерение показывает превышение ПДК или / -е изделие дефектно, и х,- = 0, если это не так. Тогда число х превышений ПДК или дефектных единиц продукции в выборке равно [c.344]
Пусть значение некоторой неизвестной величины определяется с помощью п измерительных приборов. Ошибки приборов — независимые случайные величины с одинаковым распределением и нулевым математическим ожиданием. Возникает задача усреднения показаний приборов — объединения всех измерений в одно, отвечающее минимальной дисперсии сглаженной ошибки. [c.314]
Стандартная гауссова статистика лучше всего работает на основе весьма ограничивающих предположений. Центральная предельная теорема (или Закон больших чисел) утверждает, что по мере проведения все большего числа испытаний, предельное распределение случайной системы будет нормальным распределением, или колоколообразной кривой. Измеряемые события должны быть "независимы и идентично распределены" (IID). То есть события не должны влиять друг на друга, и они все должны иметь одинаковую вероятность наступления. Долгое время предполагалось, что большинство крупных, комплексных систем должны моделироваться таким образом. Предположение о нормальности, или почти нормальности, обычно делалось при исследовании крупной, комплексной системы, так чтобы мог быть применен стандартный статистический анализ. [c.61]
Если в модели (7.2) остатки е,- не зависят от Хг-, независимы между собой, одинаково распределены и имеют распределение [c.215]
Произвольное распределение возмущений . Оценка (12.10) формально совпадает с мнк-оценкой. Так же как и в случае регрессионных задач, кажется естественным использовать ее и при распределениях возмущений е,, не совпадающих с нормальным, а лишь удовлетворяющих условиям (12.2 ), дополненным требованием их одинаковой распределенное и независимости. Оказывается [21, 1551, что в этом случае оценка (12.10) является состоятельной при любых 0, причем [c.366]
Оценки метода наименьших квадратов параметров модели авторегрессии в широком классе случаев (а именно при условии независимости, одинаковой распределенное и конечности дисперсий участвующих в них случайных возмущений е,, см. (12.2)) являются состоятельными. Асимптотические распределения оценок в устойчивом случае всегда являются нормальными, причем их дисперсия (ковариационная матрица) не зависит от дисперсии возмущений ег В общем случае (т. е. в ситуации, когда некоторые из корней характеристического уравнения (12.17) по модулю превосходят единицу) асимптотическое распределение оценок определяется распределением случайных возмущений е . Математическая модель авторегрессии /n-го порядка xt = [c.371]
Для динамических систем, рассмотренных в 4а, этот анализ показывает, что, глобальным образом, поведение Fn(x) (для "хаотических" систем с инвариантным распределением F(x)) качественно отличается от поведения Fn(x) (для "стохастических" систем, образованных независимыми одинаково распределенными величинами с одномерным распределением F(x)). Это говорит о том, что для рассматриваемых моделей максимум является хорошей статистикой в рассматриваемой проблеме различимости "хаотичности" и "стохастичности" Но, разумеется, это не исключает того, что может найтись "хаотическая" система вида хп+ = f(xn,xn-i,--. , Zn-Jt А) с достаточно большим k, которую будет трудно отличить от "стохастического белого шума" пусть и по большому, но конечному числу наблюдений. [c.229]
Для полноты картины к данным двум определениям целесообразно еще добавить третье, раскрывающее роль устойчивых распределений как тех и только тех, которые могут возникать в качестве предельных (при соответствующей нормировке и центрировании) для сумм независимых одинаково распределенных случайных величин. [c.232]
Определение 3. Случайная величина X называется имеющей устойчивое распределение (или, попросту, устойчивой), если это распределение имеет область притяжения в том смысле, что найдутся последовательности независимых одинаково распределенных случайных величин YI > 2, i последовательности положительных чисел (dn ) и действительных чисел (а ) такие, что [c.233]
Так как т, т2,. . ., тк есть независимые и одинаково распределенные случайные величины, то случайное число вагонов, находящихся на пути накопления до момента прибытия mK+i = m3H, равно 5/с==ктГр, а дисперсия этого числа вагонов D[SK] равна сумме дисперсий, т. е. D[5K] = D[/ni] + D[m2]+. .. + D[mK] = кО[тГ1)]. [c.83]
Пожалуй, самым сильным (относительно структуры распределений величин h — (hn )) является, помимо гауссовости, предположение независимости и одинаковой распределенности [c.111]
Если предположить независимость и одинаковую распределенность величин /ii,/i2,... с Е/ц = 0 и D/ц = 1, то, с вероятностью единица,
В некоторых случаях условия 4), 5) достаточно легко проверяются. Пусть, например, строки матрицы X независимы и одинаково распределены (как случайные f -мерные векторы), вектор ошибок состоит из независимых и одинаково распределенных компонент, Ее = О, X и е независимы. Иными словами, значения объясняющих переменных в каждом наблюдении выбираются из одной и той же генеральной совокупности, причем наблюдения между собой независимы и не зависят от случайных ошибок. Обозначим а = E(xtjX(j), i,j — l,...,k (эти числа не зависят от i, поскольку строки матрицы X одинаково распределены), и пусть А — (% ). Тогда по закону больших чисел plimn 00(l/n)X. X" = А, и если распределение каждой [c.152]
При л>10 уже можно воспользоваться центральной предельной теоремой, гласящей, что сумма большого числа независимых и одинаково распределенных слагаемых приближено распределена по нормальному закону. Итак, при л>10 Jfne7V(0,V ) и, значит Р(а<8п-80функция Лапласа. Отсюда следует, что при л>10 Р( Sa -S0 <л/л)=0,9973. [c.104]
Рассмотрим независимые случайные величины (векторы) a i,.. . , жп, каждая из которых имеет одну и ту же плотность f(x). Тогда мы будем говорить, что a i,.. . , хп независимы и одинаково распределены (independent identi ally distributed (i.i.d.)) или, другими словами, что они составляют (случайную) выборку (размера п) из распределения с плотностью f(x). [c.314]
Пусть i/i, 2/2 — последовательность случайных величин, не обязательно независимых или одинаково распределенных. Обозначим совместную функцию распределения у = (г/i,. . . , уп) Rn через /гп(- 7о) гДе неизвестен лишь параметр 70 истинное значение которого и будет оцениваться. Мы подразумеваем, что 7о Г, где Г (множество параметров) является подмножеством конечномерного евклидова пространства. Для каждого фиксированного у Rn вещественная функция [c.391]
Регрессионная модель должна быть построена в форме Yt = OQ + a. Xa + a.jXii + eh где е, — независимые и нормально распределенные переменные, все имеющие одинаковую дисперсию. [c.299]
В е р о я т н о с т н о - в р е м е н н ы е характеристики обслуживания з а я в о к. Часто полагают, что Srli — время обслуживания ге-й заявки (-го потока на одной п топ же фазе обслуживания для заявок потока i-ro типа независимы и одинаково распределены с нек-рой функцией распределения (ФР) BI(X). Во многих задачах предполагается, что ФР [c.117]
Построенные экологометрические модели требуют оценки их достоверности. При выполнении статистических исследований полученные данные тщательно анализируются на предмет удовлетворения их предположения о независимости случайных наблюдений, симметричности распределения, из которого получена выборка, равенства дисперсии ошибок, одинаковости распределения нескольких случайных величин и т.д. Все эти предположения могут рассматриваться как гипотезы, которые необходимо проверить. [c.57]
| Рис. 61. Равномерная плотность распределения вероятности результата измерения (7) и плотность распределения вероятности композиции двух (2) и трех (3) таких законов распределения вероятности (а - при Q = 0 б - при Q = 0,5) размахом является трапецеидальный закон. Это обстоятельство часто используется при учете дефицита информации. Рассматривая произведение большого числа характеристических функций, можно убедиться в том, что независимо от пида сомножителей оно стремится к характеристической функции, соответствующей нормальному закону распределения вероятности. Это фундаментальное положение носит название центральной предельной теоремы. На рис. 61 видно, как быстро нормализуется композиция одинаковых равномерных законов распределения вероятности. При числе слагаемых больше 4-х уже можно считать, что она практически подчиняется нормальному закону. | 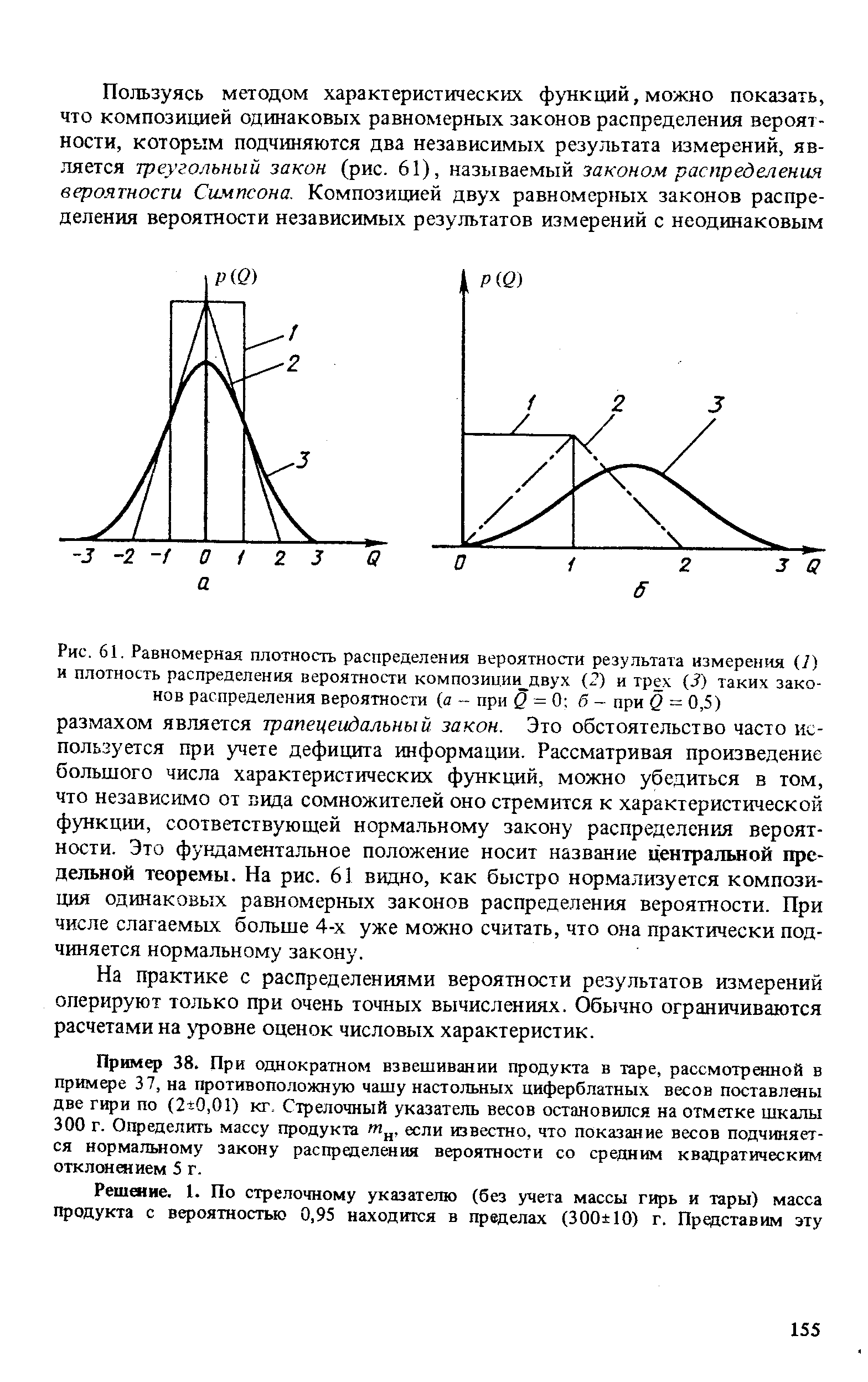 |
