Статистически говоря, временная структура волатильности показывает, что фондовый рынок не является случайным блужданием. В лучшем случае он является стохастическим "ограниченным" множеством. Это означает, что есть пределы тому, как далеко случайный ходок пройдет, прежде чем он или она направятся обратно к дому. [c.38]
Самое популярное объяснение ограниченности заключается в том, что прибыли являются возвратными к среднему. Стохастический процесс, возвратный к среднему, может произвести ограниченное множество, но не увеличивающийся коэффициент Шарпа. Возвратный к среднему процесс подразумевает игру с нулевой суммой. Исключительно высокие доходы в одном периоде нейтрализуются доходами ниже среднего в более позднем периоде. Коэффициент Шарпа остался бы постоянным, потому что прибыли также были бы ограничены. Таким образом, средняя реверсия в прибылях не является полностью удовлетворительным объяснением ограниченности изменчивости. Независимо от этого процесс, который производит наблюдаемую временную структуру волатильности, явно не гауссов, при этом он недостаточно хорошо описывается нормальным распределением. [c.38]
| Таблица 2.2 Индекс Доу-Джонса для акций промышленных компаний, результаты регрессии, временная структура волатильности 1888-1990 гг. | 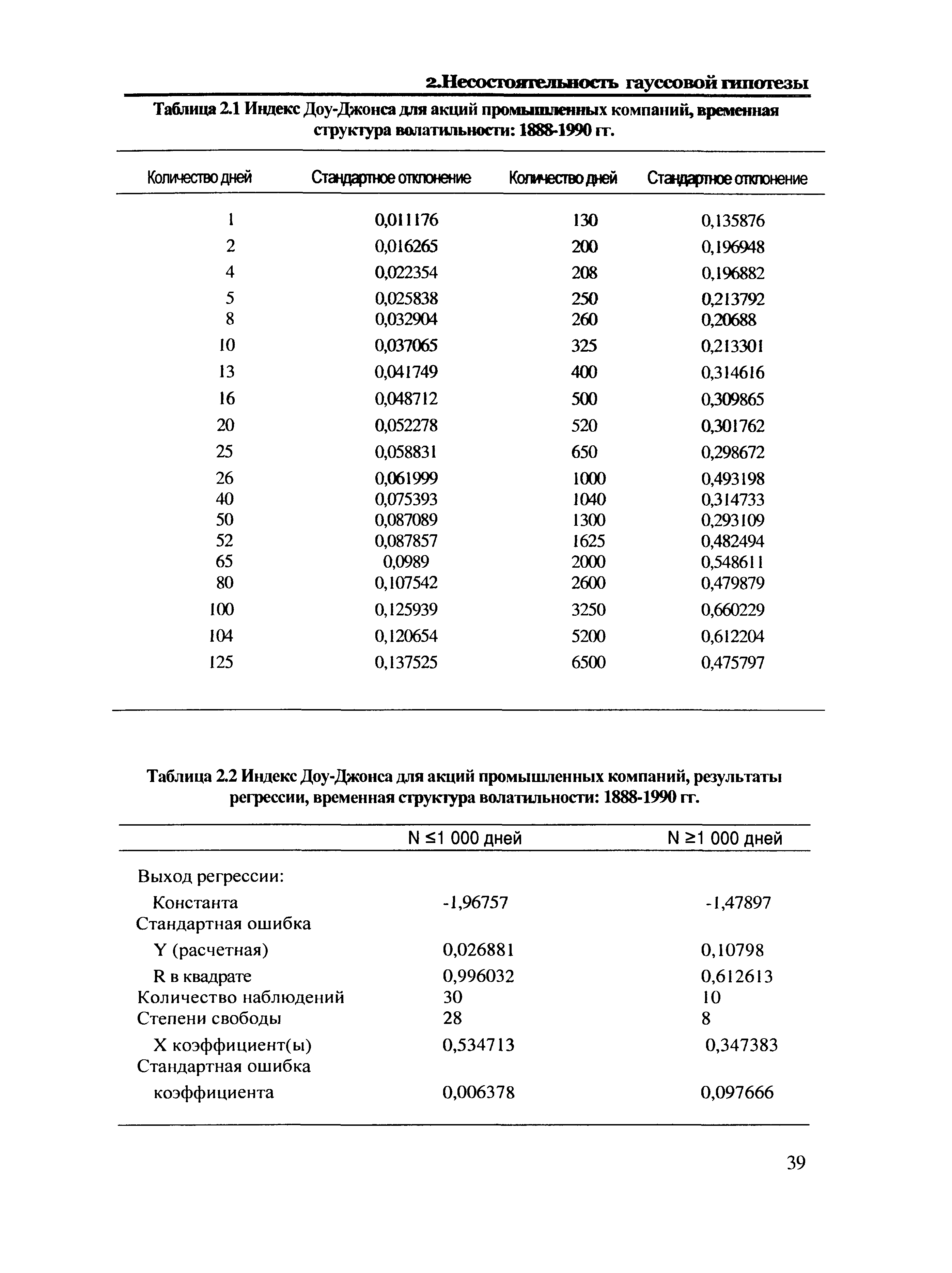 |
РИСУНОК 2.8 Ежедневные доходы по облигациям, временная структура волатильности [c.41]
| Таблица 2.4 Долгосрочные казначейские облигации, временная структура волатильности 1 января 1978 г. - 30 июня 1990 г. | 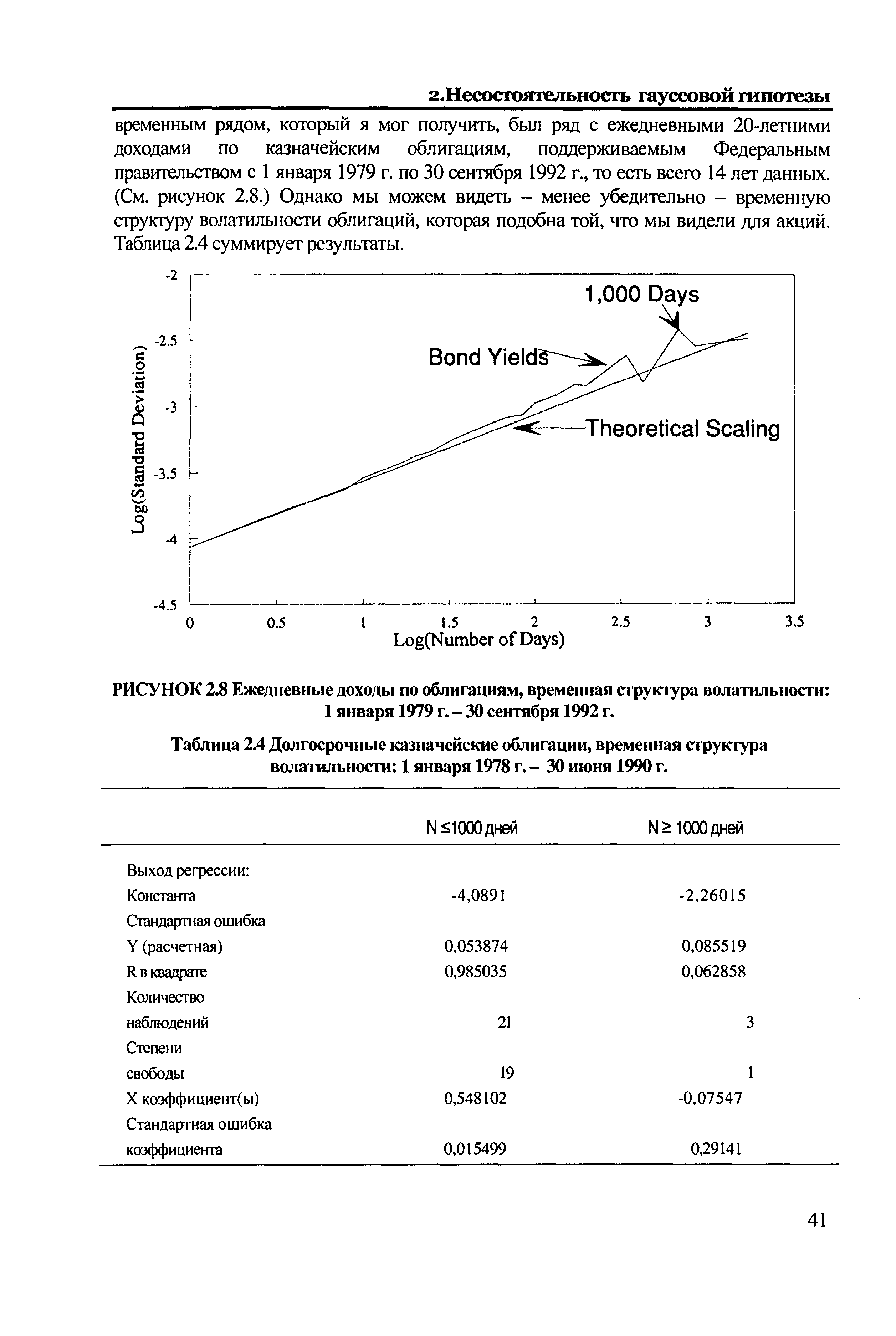 |
Чтобы исследовать, остаются ли американские акции ограниченным множеством за этот период, мы проверяем временную структуру волатильности на рисунке 2.7. Она остается ограниченной. Эти результаты включены в Таблицу 2.5. Следовательно, либо валюта имеет более длинный "ограниченный" интервал, чем акции, либо она не имеет никаких ограничений. Последнее подразумевало бы, что валютный риск растет более быстрым темпом, чем нормальное распределение, но никогда не прекращает расти. Следовательно, перед долгосрочными держателями валюты стоят постоянно возрастающие уровни риска по мере расширения их инвестиционного горизонта. В отличие от акций и облигаций валюта не предлагает [c.42]
РИСУНОК 2.10а Обменный курс марка/доллар, временная структура волатильности. [c.44]
РИСУНОК 2.11 Синусоидальная волна, временная структура волатильности. [c.46]
Рисунок 2.11 показывает временную структуру волатильности для простой [c.46]
В данный момент мы можем видеть свидетельство того, что акции, облигации, и валюта являются возможными нелинейными стохастическими процессами в краткосрочной перспективе, что подтверждается их частотными распределениями и временными структурами волатильности. Однако акции и облигации имеют признаки долгосрочного детерминизма. И снова мы видим локальную случайность и глобальный детерминизм. [c.47]
Второе свойство, которое мы наблюдали в Главе 2, касалось временной структуры волатильности. Стандартное отклонение прибыли увеличивалось более быстрым темпом, чем квадратный корень из времени. Для акций и облигаций временная структура волатильности была ограничена для валюты не было никаких ограничений. Еще раз повторю, что это важные свойства, которые должны быть объяснены. Мы должны также объяснить, почему оказывается так, что стандартная гауссова статистика иногда работает хорошо, а иногда плохо. Известно, что корреляции приходят и уходят и что волатильность является очень нестабильной. Кроме того, беты САРМ обычно стабильны, но не всегда. Спор по поводу ЕМН сбивается с толку тем фактом, что временные периоды, как может быть обнаружено, поддерживают обе стороны спора. Когда рынки считаются "стабильными", ЕМН и САРМ, кажется, работают хорошо. Однако во время паники и стихийных бегств такие модели ломаются подобно "сингулярностям" в физике. Это не является неожиданностью, потому что ЕМН и САРМ - модели равновесия. Они не могут справиться с переходом к турбулентности. Новой рыночной гипотезе понадобилась бы способность объяснить эту сингулярную характеристику торговых рынков. [c.54]
Мы видели временную структуру волатильности в Главе 2. На рынках акций, облигаций и валюты волатильность увеличивалась быстрее, чем квадратный корень времени. Это отношение одного инвестиционного горизонта к другому, усиливая эффекты меньших горизонтов, может быть динамической причиной того, что волатильность имеет свойство масштабирования степенного закона. В любой момент времени фрактальная структура рынков (то есть многих инвесторов, которые имеют различные инвестиционные горизонты, торгуя одновременно) представляет собой моментальный снимок [c.172]
В Главе 2 мы рассмотрели временную структуру волатильности рынков акций, облигаций и валюты. Временная структура волатильности - стандартное отклонение прибылей на различных горизонтах времени. Если рыночные прибыли определяются нормальным распределением, то волатильность должна увеличиться с квадратным корнем из времени. То есть пятидневные прибыли должны иметь стандартное отклонение, эквивалентное стандартному отклонению ежедневных прибылей, умноженному на квадратный корень из пяти. Однако мы нашли, что акции, облигации и валюта имеют такие временные структуры волатильности, которые увеличиваются быстрее квадратного корня из времени, что согласуется со свойствами распределений бесконечной дисперсии и дробного броуновского движения (FBM). Для чистого процесса FBM такое масштабирование должно увеличиваться бесконечно. Мы нашли, что валюта, как оказалось, не имеет предела масштабирования, но [c.244]
Концептуально, да, связь есть. В хаотической системе, аттрактор -ограниченное множество. После перемещения системы по одному циклу изменения перестанут расти. Следовательно, было бы неудивительно обнаружить, что хаотические системы также имеют ограниченные временные структуры волатильности. Фактически, ограниченные временные структуры волатильности могут быть еще одним способом проверки на наличие непериодических циклов. [c.245]
Программы приведены в их самом основном формате. Пользователи должны будут настроить их для своих прикладных систем. В данном приложении содержатся программы для вычисления R/S, E(R/S), последовательного стандартного отклонения и среднего, а также временной структуры волатильности. Обычно я беру результат этих программ и ввожу его в электронную таблицу для графического представления и непосредственной обработки. Я предпочитаю электронные таблицы из-за мгновенной обратной связи, которую я получаю в процессе преобразований. Однако тот способ, которым пользователь решает обрабатывать результат является исключительно вопросом личного предпочтения. [c.267]
Как и в программе для последовательного среднего и стандартного отклонения, программа вычисления временной структуры волатильности использует большую часть программы R/S-анализа, переформатируя данные как матрицу п X i, где п -временной интервал процента. В этом случае мы начинаем с ежедневных данных, строим вектор цен 27 002 X 1 и вычисляем стандартное отклонение изменений AR(1)-разностей. Затем мы переходим к 2-дневным данным и создаем матрицу цен 13 502 X 2. Столбец 1 теперь содержит цену каждые два дня. Затем мы вычисляем стандартное отклонение изменений АК(1)-разностей столбца 1. Мы продолжаем делать это до тех пор, пока у нас не закончатся данные. [c.272]
Временная структура. Величина переменной в различных временных интервалах. Временная структура ставки процента - это прибыль, полученная до момента погашения обязательств, для различных ценных бумаг с фиксированной доходностью при различных сроках выплаты. Временная структура волатильности — стандартные отклонения прибылей при различных временных горизонтах. [c.285]
Эта точка представляет значительно более сильную поддержку или сопротивление, чем отдельно находящийся Фиб-узел. Скопление (близость) зависит от волатильности и Временной Структуры Рыночного Размаха. Поэтому Скопления Фиб-узлов на разных графиках могут сильно различаться. Например, крайние значения ценовых диапазонов на минутном и месячном графиках отличаются очень заметно. Точно так же широко изменяется размах цен в отдельно взятой Временной Структуре. В один день мы можем иметь амплитуду колебаний цен в 250 пунктов, а в другой день - 1250 пунктов. Скопление субъективно. Этим оно смущает программистов и трейдеров, предпочитаемых механистические системы торговли, что очень хорошо для долговечности и полноценности этого подхода. [c.142]
Управление сложными портфелями, таким образом, требует применения двумерной матрицы подразумеваемой волатильности. Одно измерение — по ценам исполнения, а другое — во времени. Используемые отдельные волатильности должны отражать как можно точнее опционные цены на действующем рынке. С течением времени структура матрицы подразумеваемой волатильности может измениться, и это будет еще одним источником неопределенности, который должен быть рассмотрен. [c.202]
Статистическое исследование волатильности с помощью излагаемого далее 72/5-анализа (см. раздел 4) позволяет выявить ряд замечательных и неожиданных свойств, которые дают возможность проверки тех или иных гипотез относительно пространственно-временной структуры процессов Н = (Ht)t- o (в случае моделей с непрерывным временем) и Н — (Нп)п- о (в случае дискретного времени). Например, для многих финансовых индексов довольно определенно надо отвергнуть гипотезу о независимости величин /г , п 1, образующих последовательность Н = (Нп)п о-(В случае непрерывного времени этому соответствует отклонение гипотезы о том, что Н = (Ht)t- Q является процессом с независимыми приращениями. ) [c.420]
С опционной волатильностью связано понятие кривой волатильности. Для построения кривой волатильности выбирается определенная дата экспирации опционов и страйки, по которым ведется торговля опционами с этой датой экспирации, откладываются по горизонтальной оси. По вертикальной оси откладываются значения опционной волатильности. Если в некоторой серии опционов проходит сделка, то по величине премии и цене базисного актива рассчитывается опционная волатильность и для соответствующего страйка на графике делается отметка (при этом желательно применять обозначения, различающие сделки по опционам колл и пут). В идеале все анализируемые сделки должны быть проведены за очень короткий отрезок времени для того, чтобы получить моментальный снимок рыночной ситуации. На том же графике могут быть изображены интервалы между ценами спроса и предложения, выраженные в терминах волатильности. Как правило, точки, соответствующие сделкам по опционам колл и пут на одном страйке, оказываются близкими, а ворота между ценами спроса и предложения имеют общую часть, что объясняется пут-колл паритетом (5.6) временные составляющие премий опционов колл и пут на одном страйке для устранения арбитражных возможностей должны быть равны, следовательно, должны быть равны и опционные волатильности. Кривая волатильности получается соединением этих точек ломаной или более гладкой линией. Когда на отдельных страйках сделки отсутствуют, то применяются методы интерполяции и экстраполяции, причем во внимание принимается весь массив имеющихся данных о сделках и заявках по всем сериям опционов со всеми месяцами исполнения. Данные об имеющихся опционных волатильностях заносятся в таблицу, в которой столбцы соответствуют страйкам, а строки месяцам исполнения (так называемую матрицу волатильностей). Таким образом, учитывается и временная структура опционных волатильностей. [c.62]
Технологии, о которых идет речь, основываются на нелинейных методах анализа экономической и финансовой информации. В условиях возрастающей неуправляемости мировых процессов в финансовой сфере традиционные (читай, линейные) методы все чаще оказываются неспособными распознать ключевые переломы в тенденциях рынка. Так было, например, в случаях с крахом фондового рынка в 1987 году или началом глубокого спада в экономике Великобритании. Разочарование в этих методах заставило вспомнить о некогда казавшейся невероятной идее, согласно которой изменение рыночных показателей во времени не есть чисто случайное блуждание, а размеры ожидаемых доходов и/или характеристики неустойчивости (волатильности) можно пытаться находить при помощи более мощных методов. Общей чертой новых методов является возможность распознавания образов и вывода обобщающих правил. Существенными составными частями нового подхода являются нейронные сети (сети компьютерных процессоров, взаимодействие которых построено по образцу процессов обучения, происходящих в человеческом мозге) и генетические алгоритмы (методы, в которых, исходя из большого набора первоначальных предположений, вырабатывают все более правильные представления о поведении рынка и, в конечном счете, более содержательные рабочие гипотезы). Про методы обоих видов говорят, что они управляются данными, в противоположность подходу, основанному на применении правил, который принят в экспертных системах. Системы, основанные на знаниях, обладают тем недостатком, что построенные на их основе методы торговли оказываются довольно негибкими. Наконец, совершенно новый взгляд на мир предлагает теория динамических систем или теория хаоса. С ее помощью в явлениях, ранее считавшихся случайными, удается обнаружить порядок или некоторую структуру. Основное предположение здесь состоит в том, что поведение системы есть результат множества нелинейных взаимодействий, вследствие чего даже небольшое изменение начальных данных может привести к совершенно другому дальнейшему поведению системы. Благодаря [c.13]
Таким образом, при возможности регистрации значений процесса Я = (Ht)t o только в дискретные моменты времени п = 1,2,... наблюдаемая последовательность значений hn = Нп —Нп- имеет совсем простую структуру гауссовской последовательности (<7n n)n i независимых случайных величин с нулевым средним и, вообще говоря, "неоднородными" (волатильностями) дисперсиями <т . [c.429]
Разделение смещений, вызванных замещением, на две группы (для верхнего и нижнего уровней построения индекса цен), обусловлено следующими соображениями. Прежде всего, при построении элементарных агрегатов возникают более серьезные проблемы с формированием систем весов, которые используются в индексных формулах. При построении сводных индексов потребительских цен веса могут быть основаны на информации о структуре потребительских расходов, полученной на базе обследований бюджетов домашних хозяйств. Для построения же элементарных агрегатов необходима гораздо более детализированная информация такого рода, которая обычно бывает известна с гораздо меньшей точностью. Это приводит к тому, что точность весов, используемых при построении элементарных агрегатов, обычно значительно уступает точности весов, используемых при построении сводных индексов цен. Помимо этого, временные ряды индивидуальных индексов цен, на основе которых строятся элементарные агрегаты, имеют большую волатильность по сравнению с временными рядами элементарных агрегатов, используемых при построении сводных индексов цен, поскольку менее агрегированные данные вообще более волатильны по сравнению с соответствующими им агрегированными данными. Все это приводит к тому, что использование одних и тех же индексных формул порождает больше проблем при построении элементарных агрегатов, чем при построении сводных индексов цен. [c.21]
Другое основное предположение, которое необходимо для применения нормального распределения, затрагивает временную структуру волатильности. Как правило, мы используем стандартное отклонение для измерения волатильности и предполагаем, что она подвергается масштабированию согласно квадратному корню из времени. Например, мы "пересчитываем на год" стандартное отклонение ежемесячных прибылей посредством умножения его на квадратный корень из 12. Эта практика происходит из наблюдения Эйнштейна (Einstein, 1905), что расстояние, которое проходит частица в броуновском движении, увеличивается с квадратным корнем из времени, затраченного на его измерение. [c.37]
Временная структура волатильности оказалась даже более странной, чем думали эти исследователи. Рисунок 2.7 - график логарифма стандартного отклонения против логарифма времени относительно 103-летних данных ежедневного индекса Доу-Джонса для акций промышленных компаний. Эта диаграмма была построена посредством равномерного разделения полного 103-летнего периода на все подынтервалы, которые включали и начальные, и конечные точки. Поскольку число используемых подпериодов зависит от общего количества точек, был использован интервал в 25 000 дней. Были рассчитаны прибыли для смежных периодов, а также были рассчитаны стандартные отклонения этих прибылей. Результаты приведены в Таблице 2.1. Таким образом, мы имеем подпериоды в пределах от 25 000 однодневных прибылей до четырех 6.250-дневных прибылей, или приблизительно 28 лет. [c.37]
РИСУНОК 2.10с Обменный курс иена/фунт, временная структура волатильности. Таблица 2.5 Обменные курсы валют, временная структура волитальности [c.45]
Исходя из вышеупомянутого анализа, 20-дневные изменения в цене по индексу Доу-Джонса характеризуются как персистентный процесс Херста с Н = 0,72. Это значительно отличается от результата для случайных блужданий. Поскольку ряд состоит из АК.(1)-разностей, мы знаем, что работает истинный процесс с долговременной памятью. Характеристики этого ряда имеют мало общего с другими стохастическими процессами, исследованными в Главе 4. Особенно они отличаются от рядов AR H и GAR H (см. Главу 4), которые так часто использовались в качестве моделей рыночных процессов. Однако персистентное масштабирование действительно имеет предельный срок. Оно происходит только в течение тех периодов, которые короче 1 000 операционных дней. Поэтому данный процесс является не процессом бесконечной памяти, а длинной, но конечной памятью с непериодическим циклом, составляющим приблизительно четыре года. Четырехлетний цикл может быть связан с экономическим циклом. Он также кажется связанным с временной структурой волатильности, исследованной в Главе 2. Масштабирование волатильности также прекратилось после четырех лет. [c.116]
На рынке валюты мы видим как раз такие характеристики. В Главе 2 мы видели, что временная структура волатильности для обменного курса иена/доллар отличалась от таковой для американских акций и облигаций. В Главе 4 мы рассмотрели признаки персистентного показателя Херста для обменного курса иена/доллар. В этой главе мы исследуем этот и другие обменные курсы более подробно. Исследование будет все еще ограниченно. [c.158]
В таблице 12.1 приводятся результаты, а на рисунке 12.1 показан график V-статистики для этой валюты. Показатель Херста выше значения для ежедневных американских акций, при этом Н = 0,64. Этот период имеет 5 200 наблюдений, так что оценка более чем на три стандартных отклонения выше ее ожидаемого значения. Следовательно, она в высокой степени перситентна по сравнению с фондовой биржей. Однако не видно никакого долгосрочного цикла. Это согласуется с временной структурой волатильности, которая также не имеет очевидного снижения риска. Поэтому мы можем сделать вывод, что обменный курс иена/доллар совместим с дробным броуновским движением, или процессом Херста. Однако в отличие от рынка акций и облигаций не наблюдается переход к долговременной "фундаментальной" оценке. На всех инвестиционных горизонтах продолжает доминировать техническая информация. На основании этого мы могли бы предположить, что этот процесс является истинной "бесконечной памятью", или процессом Херста, в противоположность процессу с долгой, но конечной памятью, который характеризует рынки акций и облигаций. [c.159]
FBM не совместимо с одним аспектом рынков, таких как рынок акций и облигаций. Долгосрочные инвестиции никак не вознафаждаются. Мы видели в Главе 2, что акции и облигации характеризуются возрастающими соотношениями доходность/риск через четыре года. FBM, с другой стороны, не имеет офаниченных характеристик риска то есть временная структура волатильности, теоретически, не прекращает расти. [c.225]
Рисунок 17.4(а) показывает временную структуру волатильности уравнения Макки-Гласса с задержкой в 50 итераций. Масштабирование останавливается как раз перед 50 итерациями. Рисунок 17.4(Ь) показывает временную структуру волатильности для уравнения Макки-Гласса с добавленным наблюдаемым и системным шумом. Это те же самые временные ряды с добавлением шума, которые используются на протяжении всей книги. Они оба имеют Н 0,70 против Н = 0,92 для версии без шума. Ряды с добавленным шумом еще более убедительны, чем аттрактор Макки-Гласса без шума. Пик на обоих графиках происходит, несомненно, при п = 50 итераций, то есть среднем непериодическом цикле системы. [c.245]
Я провел подобный анализ для аттракторов Лоренца и Росселера. Я призываю читателей самим пробовать этот анализ, используя программу, приведенную в Приложении 2 или собственную программу. Временная структура волатильности этих хаотических систем имеет поразительное сходство с аналогичными графиками рынков акций и облигаций, приведенными в Главе 2. Валюта не имеет этой офаниченнои характеристики - еще одно свидетельство того, что валюта является не "хаотическим" процессом, а, вместо этого, процессом дробного шума. Это не подразумевает, что валюта не имеет интервалов изменения очевидно, что она их имеет, но у этих интервалов изменений нет средней длины. Что касается валюты, джокер действительно появляется случайным образом, что же касается американских акций и облигаций, джокер имеет среднюю частоту появления, составляющую четыре года. [c.246]
Когда опционы дешевы, причины это могут быть гораздо менее заметны. Наиболее обычной причиной может быть то, что, возможно, изменилась корпоративная структура компании - компанию кто-то приобрел или компания приобрела другую компанию почти соответствующую ей по размеру. В любом случае, возможно, что акция объединенной корпорации будет менее волатилъна, чем была акция первоначальной компании. Поскольку поглощение находится в процессе, который требует времени, подразумеваемая волатильность опционов на акции компании понизится, создавая ложное впечатление, что они являются дешевыми. [c.220]
Индекс относительной силы (Relative Strength Index, RSI) этот технический индикатор, помогающий измерять силу цены акции или индекса по отношению к их прошлому поведению, в значительной степени основывается на предпосылке, что RSI достигает вершины или основания прежде, чем рынок формирует свою реальную вершину или основание. Таким образом, RSI рассматривается многими трейдерами как сигнал возможного предстоящего разворота. Значения RSI более 70 обычно интерпретируются как перекупленность, а ниже 30 указывают на перепроданность. RSI, как и скользящие средние, могут применяться в различных временных структурах. Как правило, чем короче временная структура, тем волатильнее RSI. [c.43]
FibNodes не зависит от источника информации. Эта программа не использует базу данных или онлайновую службу, чтобы поддерживать свои файлы. Вы просто вводите соответствующие значения. Программа обсчитывает и хранит введенные данные, предоставляя информацию об уровнях поддержки и сопротивления, как это описано в Уровнях ДиНаполи. Если рынок достигает нового максимума или минимума, либо если требуется ввод нового Номера Реакции, вы добавляете только этот Номер, и программа использует уже сохраненные в файле данные, чтобы повторно рассчитать все подходящие точки. Представление включает Происхождение, однако Скопления не определяются автоматически, так как Временная Структура и волатильность на данном рынке могут обеспечить несоразмерно обширные области Скопления, включая их местоположение. [c.277]
Обращаясь к другой главной теме, освещенной автором - к "продаже волатильности", надо заметить, что здесь - представлено решение исключительно важной задачи, связанной с управлением риском коротких опционных позиций. Все торговцы, имеющие склонность к коллекционированию временной стоимости, которая обеспечивает чрезвычайно высокую доходность в спекулятивной торговле, знают насколько грандиозной может быть плата за принимаемый риск. Коннолли и здесь предлагает свое решение данной проблемы, что коренным образом изменяет структуру стратегии. Все становится простым и понятным есть прогнозируемый риск, и существует плата за него. [c.234]
Мы хотим установить доверие к применению геометрических торговых инструментов Фибоначчи, объясняя, как они работают на различных продуктах и в различных рамках времени, не меняя своей структуры. Неприемлемо, когда инструмент срабатывает лишь однажды, в особой ситуации на рынке, и затем теряет свою силу, когда ценовые фигуры и торговая среда изменяются. С очень немногими исключениями, все шесть геометрических торговых приспособлений Фибоначчи, представленные в данной книге, сохраняют надежность независимо от торгового продукта или рамок времени, используемых в анализе. Единственные требования для анализа Фибоначчи — волатильность и продаваемость. [c.230]
В сущности их задача состоит в попытках обеспечить высокую доходность инвестиций — скажем, 10% в год и более — на фоне не очень сильно выраженной волатильности. И все же в настоящее время не многим фондам удается справиться с этим. Одна из причин — их структура. Хеджевые фонды не сталкиваются с проблемами, касающимися выкупа акций, чего не скажешь о специализирующихся на коротких / длинных позициях. Время от времени они располагают избыточным средствами для инвестирования, но бывают и периоды, когда им приходится продавать акции, чтобы выкупить у инвесторов свои. [c.303]
Следует отметить, что по характеру своего поведения предполагаемая волатилъность схожа с эмпирической волатильностью, определяемой (в случае непрерывного времени) по формулам типа (8). При этом весьма четко прослеживается ее отрицательная коррелированность и фрактальная структура (см., например, [386 гл. 10]). [c.417]
Смотреть страницы где упоминается термин ВРЕМЕННАЯ СТРУКТУРА ВОЛАТИЛЬНОСТИ
: [c.41] [c.44] [c.114] [c.245] [c.420] [c.513]Смотреть главы в:
Фрактальный анализ финансовых рынков -> ВРЕМЕННАЯ СТРУКТУРА ВОЛАТИЛЬНОСТИ
