Прежде всего для простоты часто предполагают, что количество товаров может изменяться непрерывно, т. е. элементы вектора у могут принимать любые неотрицательные значения. Далее предполагают, что функция и(у) меняется непрерывно и имеет все необходимые частные производные. Эти предположения по своей природе аналогичны соответствующим предположениям о производственных функциях и имеют математическую природу. [c.116]
Приравнивая производную к нулю, получим выражение для определения вектора оценки а [c.326]
На основании необходимого условия экстремума функции нескольких переменных S(bo, b, ..., bp), представляющей (4.3), необходимо приравнять нулю частные производные по этим переменным или в матричной форме — вектор частных производных [c.84]
Очевидно, что вектор производных характеристик у при таком задании является функцией от вектора исходных характеристик [c.146]
При рассмотрении химического равновесия те же соображения о максимуме суммарной энтропии при заданном суммарном количестве каждого из компонентов в системе приводят к условию равенства производных энтропии каждой из подсистем по числу молей в ней г -го вещества, т.е. к равенству векторов химических потенциалов //г-. [c.27]
Так как производные в (9.241) представляют собой не что иное, как значения множителей Лагранжа А в задачах 1 и 2 соответственно, то из (9.241) следует, что векторы множителей Лагранжа в этих задачах, а следовательно, и в выражениях (9.229) и (9.230), равны друг другу. [c.392]
Поскольку r(u,v)/(u2 + v2)1/2 — > 0 при (u,v) — > (0,0), 0 дифференцируема всюду на R2, и ее производная равна вектор-строке (т/2, 2ху). [c.120]
Вектор а, если он существует, является, конечно, производной Оф(с). Таким образом, дифференцируемость определяется посредством разложения Тейлора первого порядка. [c.143]
Безусловно, определение 2 имеет некоторые достоинства. Во-первых, если F является матричной функцией только одной переменной , то dF( )/д имеет тот же размер, что и F( ). Во-вторых, если ф — скалярная функция матрицы X, то размер дф(Х /дХ снова совпадает с размером X. В частности, если ф — скалярная функция вектор-столбца ж, то дф/дх — вектор-столбец, а дф/дх — вектор-строка. Кроме того, это определение предлагает четыре способа для упорядочения тп частных производных векторной функции f(x) размера т х 1, где х — вектор переменных размера п х 1 df/dx (матрица размера га х n), df /dx (матрица размера п х га), df/dx (тп х 1 вектор) и df /dx ( 1 х ran вектор). [c.225]
Пусть ф есть скалярная функция от п х 1 вектора х. Мы уже встречались с производной ф, определяемой как [c.226]
При предположениях, сделанных в 11, покажите, что производная собственного вектора и(Х) в точке XQ равна [c.237]
Пусть Ъх (f) непрерывная вектор-функция с кусочно непрерывной производной, а ф (t) — вектор-функция, которая может иметь конечное число разрывов первого рода (ниже для простоты предположим, что ф (t) имеет лишь один разрыв в точке t ). Тогда имеет место тождество ) [c.32]
Читатель, видимо, уже заметил, что числовые величины функциональных производных зависят не только от единиц измерения F(, но, если управление есть вектор-функция, и от единиц измерения различных ее компонент. [c.175]
Здесь L (и) — линейный дифференциальный оператор, коэффициенты которого зависят от управления и (t) Q (и) — матрица 4 ->4, х= х1, хг, х3, х1 . Конкретные выражения для /, Q и краевых условий Гх=0 см. в 11. Мы будем придерживаться стандартного обозначения независимого аргумента буквой t, хотя в данной задаче это не время, а пространственная координата. Задача (1) рассматривается на интервале [О, Т]. Управлением является трехмерная вектор-функция и( )= иъ u%, и3 , определенная на интервале [7 , Т2] С [О, Т], ее компоненты — концентрации в данной точке t трех характерных веществ замедлителя (иг), горючего (ма) и поглотителя (иа). Разумеется, коэффициенты L (и) и Q (и) зависят и от других компонент конструкции, но они в данной задаче не варьируются и явно в постановку задачи не входят. Правда, в связи с их наличием следовало бы, чтобы быть более аккуратным, использовать обозначения типа Q (и, t), но мы этого не делаем ради простоты. Вычисление производных тех функционалов, в терминах которых будут ставиться различные задачи, разъяснено в 11. Кроме того, в задаче имеются и геометрические ограничения допустимых значений компонент управления [c.329]
Особо подчеркнем, что система следования может быть применена и по отношению самого графика дополнительного измерения эффективности следования за вектором сигнала . В этом смысле можно говорить о следовании за вектором эффективности системы следования . Результаты этого будут отражены в дополнительном измерении уже второго уровня производности (первый уровень производности — это дополнительное измерение эффективности системы следования за тем, как срабатывает сигнал). [c.236]
| Рисунок 63. Дополнительное измерение полной системы следования за вектором < измерении второго порядка производности | 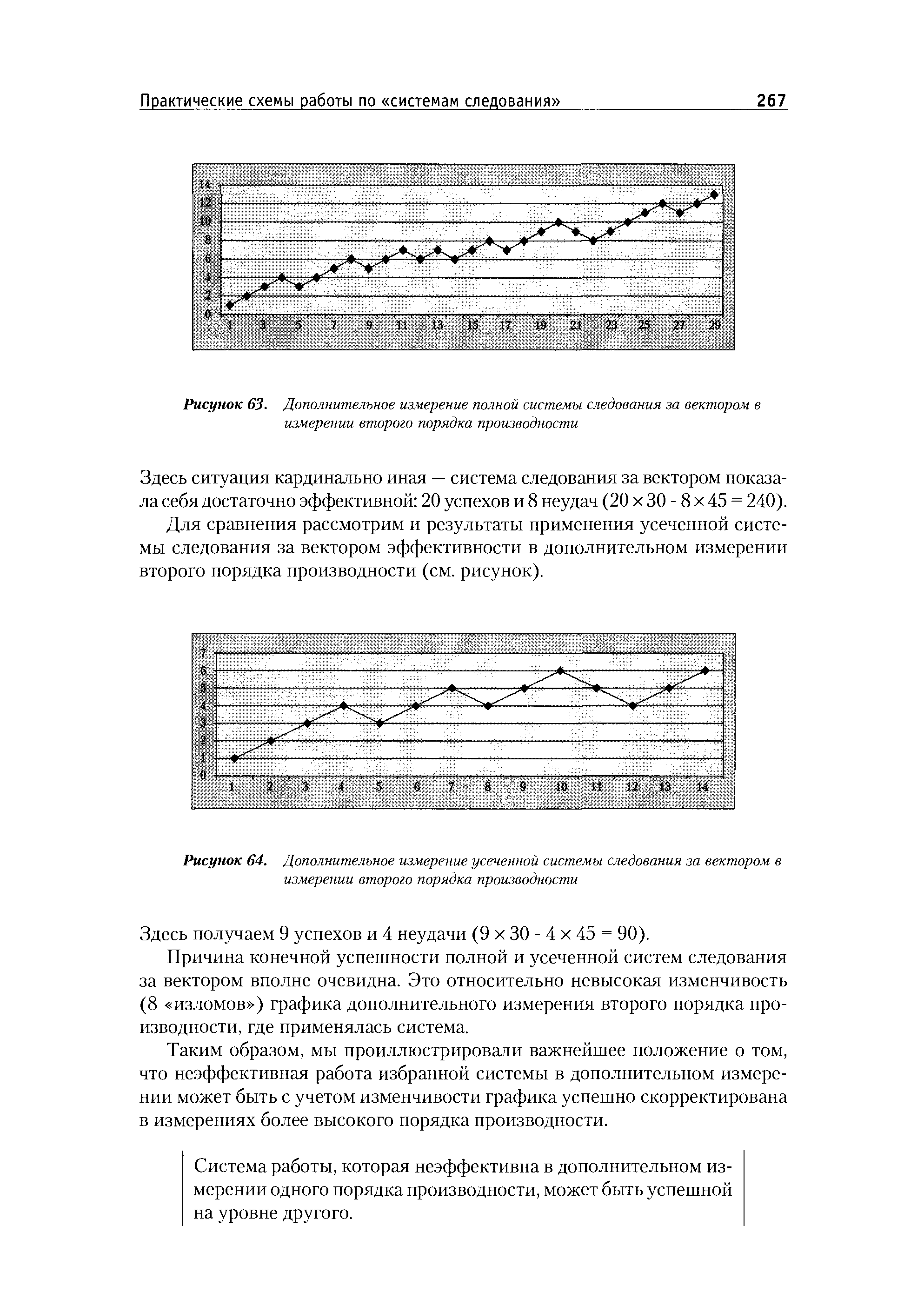 |
| Рисунок 64. Дополнительное измерение усеченной системы следования за вектором в измерении второю порядка производности | 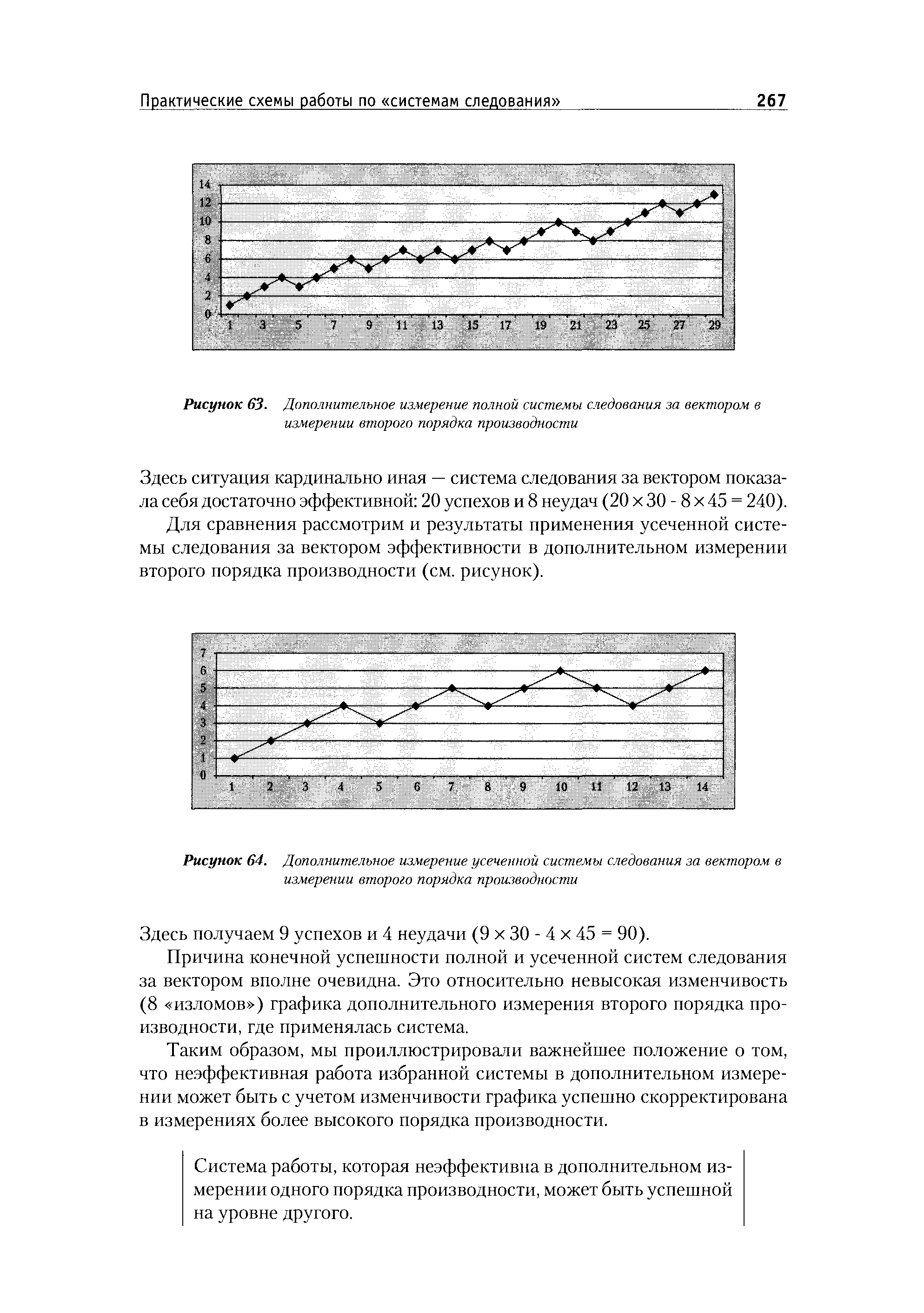 |
Если применить усеченную систему следования (операции только в направлении вверх ) и только за вектором эффективности в этом измерении второго порядка производности, то получим следующий результат, который отражен в дополнительном измерении третьего порядка производности (см. рисунок). [c.270]
Х У = (Q X Y) - Y e. Дифференцируя (11.8) по в и приравнивая полученный вектор -столбец производных [c.338]
Получить такой максимальный доход будут стремиться все предприятия. Для этого им надо сработать так, чтобы вектор системы показателей деятельности обеспечил бы выход на желаемый результат, соответственно, векторы Bi, B2 и В3. Однако в связи с тем, что оценочные критерии деятельности предприятий (максимум дохода) не совпадают с глобальным критерием оптимальности функционирования народного хозяйства и не являются производными от последнего, сумма частных локальных решений не обеспечит общего народнохозяйственного оптимума. Другими словами, как это видно из рисунка, можно утверждать, что стремление предприятий получить как можно больший доход приведет к тому, что не удастся получить максимально возможный в данных условиях развития производительных сил общества нацио-нальный доход, т. е. выйти на уровень — Я0. [c.77]
Если функция f(x) дважды непрерывно дифференцируема, условие вогнутости эквивалентно требованию неположительной определенности матрицы вторых производных функции f(x] при всех положительных значениях вектора ресурсов х, т. е. эквива-лентио требованию [c.74]
Для производственной функции (3.18) выполняется первое предположение предыдущего параграфа. Рассмотрим некоторые-другие свойства этой функции. Поскольку функция (3.18) не-диффереицируема (хотя н непрерывна), то производные выпуска по ресурсам можно рассматривать только в отдельных областях пространства ресурсов. Это делает исследование в случае большого числа ресурсов довольно громоздким, поэтому остановимся на анализе функции с двумя ресурсами н х° = (I, 1), т. е. на функции (3.17), которая сохраняет все основные черты фушщии (3.18) с произвольным числом ресурсов и произвольным вектором х°. Для функции (3.17) точки рациональных пропорций между ресурсами лежат на луче ОД. (см. рис. 2.10). [c.93]
Для вектора частных производных доказаны следующие формулы1 ( 11.10) [c.84]
ГРАДИЕНТ [gradient] — вектор, направленный в сторону наискорейшего возрастания функции и равный по величине ее производной в этом направлении [c.66]
В различных экономических приложениях применяются (и рассматриваются в словаре) следующие функции Взвешивающие, Дифференцируемые, Гладкие, Кусочно-линейные, Кусочно-непрерывные, Линейные, Нелинейные, Непрерывные, Се-парабелъные, Экспоненты и др. См. также Вектор-функция, Гессиан, Интеграл, Мультипликативная форма представления функции, Производная, Рекурсия, Частная производная, Эластичность функции. [c.379]
Начальные условия для (2.4.10) s =, so при t = 0. Граничные условия на горизонтальных границах области интегрирования —X х X, — Y у Y и на верхней границе при z = Z ставятся следующим образом. В тех точках границ, где вектор скорости направлен внутрь области определения решения, s = 8ф. Там, где вектор скорости направлен вовне этой области, значения концентраций экстраполируются на границу по приграничным значениям со вторым порядком аппроксимации. На нижней границе при z = А ставится граничное условие третьего рода, учитывающее поглощение и отражение примеси. Здесь SQ и вф — заданные значения. Уравнение (2.4.10) решается численным интегрированием в декартовой прямоугольной системе координат с применением метода фиктивных областей. Конечно-разностные аппроксимации производных по пространственным переменным построены на основе интегро-интерполяционного метода [Марчук, 1980]. Аппроксимация задачи по времени построена с помощью двуци-клического полного расщепления. Используемая схема покомпонентного расщепления дает решение для некоммутативных операторов со вторым порядком аппроксимации по времени и координатам. Для численной реализации конечно-разностных уравнений использована немонотонная прогонка. [c.116]
В основу понятия обобщенного решения могут быть положены самые различные подходы. Это интегральные законы сохранения, метод искусственной вязкости, способ предельного перехода в разностных аппроксимациях, аппарат теории обобщенных функций, понятие потенциала решения, а также другие схемы [Рождественский и др., 1978 Годунов, 1979]. Так, авторы [Васильев и др., 1987] при рассмотрении одномерного варианта (га = 1) задачи (4.4.3)-(4.4.7) для определения обобщенного решения использовали свойство эквивалентности на гладких (классических) решениях дифференциальной системы, построение которой базируется на использовании широко известного аппарата метода характеристик. Суть этого подхода заключается в диагонализации матрицы А системы (4.4.3) с помощью линейного невырожденного преобразования переменных х в инварианты Римана. После такого преобразования в каждом из уравнений системы участвуют частные производные по s и t лишь одной инварианты Римана, что позволяет рассматривать дифференциальный оператор инвариантной системы как п -мерный вектор обыкновенных производных вдоль соответствующих характеристик (аналог производной по направлению). К сожалению, возможности использования данного понятия обобщенного решения по существу [c.335]
Условия (9.127) при соответствующем выборе вектора А могут быть выполнены для произвольной дважды дифференцируемой в нуле функции /о, при этом второе условие для функций /Q с ограниченными вторыми производными может быть выполнено для всех значений С. Таким образом, можно расчитывать, что для широкого класса задач решения уравнений (9.122) существуют. [c.358]
Обозначения. В книге мы используем, в основном, стандартные обозначения, за исключением того что векторы обозначены простым (не полужирным) курсивом. Специальные символы используются для обозначения производной (матрицы) D и матрицы Гессе Н. Оператор дифференцирования обозначается как d. Полный список всех символов, использованных в тексте, содержится в Указателе обозначений в конце книги. [c.17]
Для вещественной функции ф от п х 1 вектора ж в 6.3 была введена матрица Гессе — п х п матрица частных производных второго порядка 0 0(ж), обозначаемая следующим образом [c.244]
Если супремум в (3) достигается во внутренней точке множества Г и Ьп(т) дифференцируемая по 7 функция, то вектор производных [c.392]
Пусть функция h(x) определена на /"-мерном евклидовом пространстве Rr, Обозначим через dh(x) вектор первых частных производных h по х, а через Hh(x) —матрицу Гессе h, т. е. матрицу вторых частных производных h по х. [c.357]
Рассматривалась задача типа (1) с вектор-функцией х ( ), краевые значения которой могли быть полностью или частично заданы, вариационные задачи для функций нескольких независимых переменных — в этом случае функционал вычислялся через значения частных производных искомой функции. Наконец, изучались изопериметрические задачи, в которых, кроме минимизируемого функционала F [х ( )], определялись функционалы F [x ( )],.... . ., Fm [x ( )] того же типа (1), и на искомую функцию накладывались условия вида [c.23]
Здесь W (t) — матрица г - т -(- 1, i-я строка которой-является г-мер-ной вектор-функцией ifff(t), производной функционала Ff[u(-J W (t) называют матрицей влияния она позволяет вычислить влияние малого возмущения управления на положение изображающей точки F [и ( ) - - 8м ( )] в Ет+1 (вычислить, разумеется, лишь в первом порядке, с точностью до О( 8и 2)). Таким образом, формула (10) определяет отображение конуса всевозможных вариаций управления Ки в конус смещений Кр то, что все SF образуют конус — очевидно если смещение ЬР соответствует вариации ц ( ) Ки, то смещение XS.F (где X > 0) соответствует вариации >8и ( ) 6 Ки-Очень важна для дальнейшего [c.44]
Конус смещений Кр строится о ычным образом вычислив производные всех входящих в постановку задачи функционалов F0, Flt. .., Fm[u( )], получаем для вектора смещения ЪР= ЪРа, 8F,,. .., FJ формулу [c.63]
