Для анализа стохастических моделей, особенно многокритериальных, в последнее время широко используется подход имитационного типа, получивший название метода Монте-Карло. Он состоит в следующем с помощью специально реализованного в ЭВМ генератора случайных чисел строят последовательность чисел г/ , г/2, . ., UN, которые в совокупности можно интерпретировать как последовательность реализаций случайной величины у. Выбирают конечное число вариантов управления xt, xz,. . ., хп. Рассчитывают значения W(xt, ys) для всех i = 1,. . ., п j = 1,. ... . ., N. Числа W(xi, z/j) (/ = 1,. . ., N) дают представление о распределении показателя W при управлении xt, т. е. о функции распределения FXi(r ), и могут использоваться для оценки этого [c.155]
Для того чтобы хорошо оцепить распределение FXi(r ), необходимо взять достаточно большое значение. /V — числа реализации случайной величины у. Чтобы хорошо аппроксимировать множество всех решений X, приходится брать большое число п. Это приводит к очень большому (п X N) числу расчетов, что делает метод Монте-Карло не всегда реализуемым на практике. Все же, несмотря на описанный недостаток, метод используется очень часто, поскольку является во многих случаях единственным пригодным средством анализа модели. [c.155]
Наиболее распространенными методами анализа рисков являются анализ чувствительности (уязвимости), анализ сценариев и моделирование рисков по методу Монте-Карло. [c.322]
МЕТОД МОНТЕ-КАРЛО. Этот метод воссоединяет методы анализа чувствительности и анализа сценариев на базе вероятностного подхода. Он достаточно сложен, его реализация возможна только при помощи компьютера. Итог такого анализа — распределение вероятностей возможных результатов проекта (например, вероятность получения А/РУ < 0), на основании чего принимают решение о степени рисковости данного проекта. [c.323]
Наиболее сложным, трудоемким и дорогостоящим методом анализа рисков является метод Монте-Карло. Он, в основном, используется для анализа рисков крупных проектов в условиях недостаточного объема априорной информации. Этот метод заключается в построении имитационных моделей, позволяющих создать множество сценариев, согласующихся с заданными ограничениями на исходные переменные. [c.281]
Короче говоря, менеджеры по возможности избегают черных ящиков и платят любому, кто может им помочь заглянуть внутрь. Поэтому консультанты и ученые разработали методики, которые мы будем называть анализом проекта. Несколько методик мы рассмотрим в этой главе, в первую очередь - анализ чувствительности, анализ безубыточности, модель Монте-Карло и "древо решений". В этих терминах нет ничего магического, они воплощают в себе лишь здравый смысл, подкрепленный возможностями компьютера. Вам не нужна лицензия, чтобы ими пользоваться. [c.233]
В анализе чувствительности вы единовременно меняете значение лишь одной переменной когда вы проводите анализ сценариев, вы рассматриваете ограниченное число альтернативных комбинаций переменных. Если вы хотите провести основательный анализ и рассмотреть все возможные комбинации переменных, вам, чтобы охватить все, вероятно, потребуется модель Монте-Карло. В этом случае вы должны построить полную модель проекта и определить вероятностное распределение каждой составляющей потока денежных средств. Затем вы даете компьютеру задание выбрать наугад значение каждой из этих составляющих и вычислить возможные результирующие потоки денежных средств. После того как компьютер выполнит эту операцию тысячу или примерно столько раз, вы должны получить ясное представление об ожидаемом потоке денежных средств для каждого года и разброс значений возможных потоков денежных средств. [c.256]
Предположим, что менеджер уже рассчитал потоки денежных средств проекта, определил его чистую приведенную стоимость и провел анализ чувствительности, аналогичный представленному в таблице 10-2. Перечислите дополнительные шаги, необходимые для построения модели Монте-Карло для денежных потоков проекта. [c.258]
Большинство менеджеров интересует не только ожидаемая прибыль они хотят также знать, что случится, если где-то произойдет срыв. Методы, которые мы использовали в главе 10 для оценки отдельного проекта, подходят и для рассмотрения фирмы в целом. Например, прежде чем фирма приступит к выпуску долговых обязательств на крупную сумму, ее финансовые менеджеры проводят анализ безубыточности. Иначе говоря, они смотрят, на сколько могут упасть объем продаж и прибыли, не подвергая опасности способность фирмы обслуживать долг. Или они смотрят, в каком положении окажется фирма при осуществлении ею альтернативного сценария. Или же они строят модель Монте-Карло, чтобы оценить в целом разброс возможных финансовых последствий. [c.486]
Наиболее часто встречающимися методами количественного анализа рисков проекта, как уже отмечалось, являются анализ чувствительности (уязвимости), анализ сценариев и имитационное моделирование рисков по методу Монте-Карло. [c.213]
Метод моделирования Монте-Карло, используемый для анализа рисков, представляет собой синтез методов анализа чувствительности и анализа сценариев. Это сложная методик , имеющая только компьютерную реализацию. Результатом такого анализа выступает распределение вероятностей возможных результатов проекта (например, вероятность получения NPV<0). [c.218]
Как уже отмечалось, анализ рисков с использованием метода имитационного моделирования Монте-Карло представляет собой интеграцию методов анализа чувствительности и анализа сценариев на базе теории вероятностей. [c.243]
| Рис. 7.6. Анализ рисков (по методу Монте-Карло) | 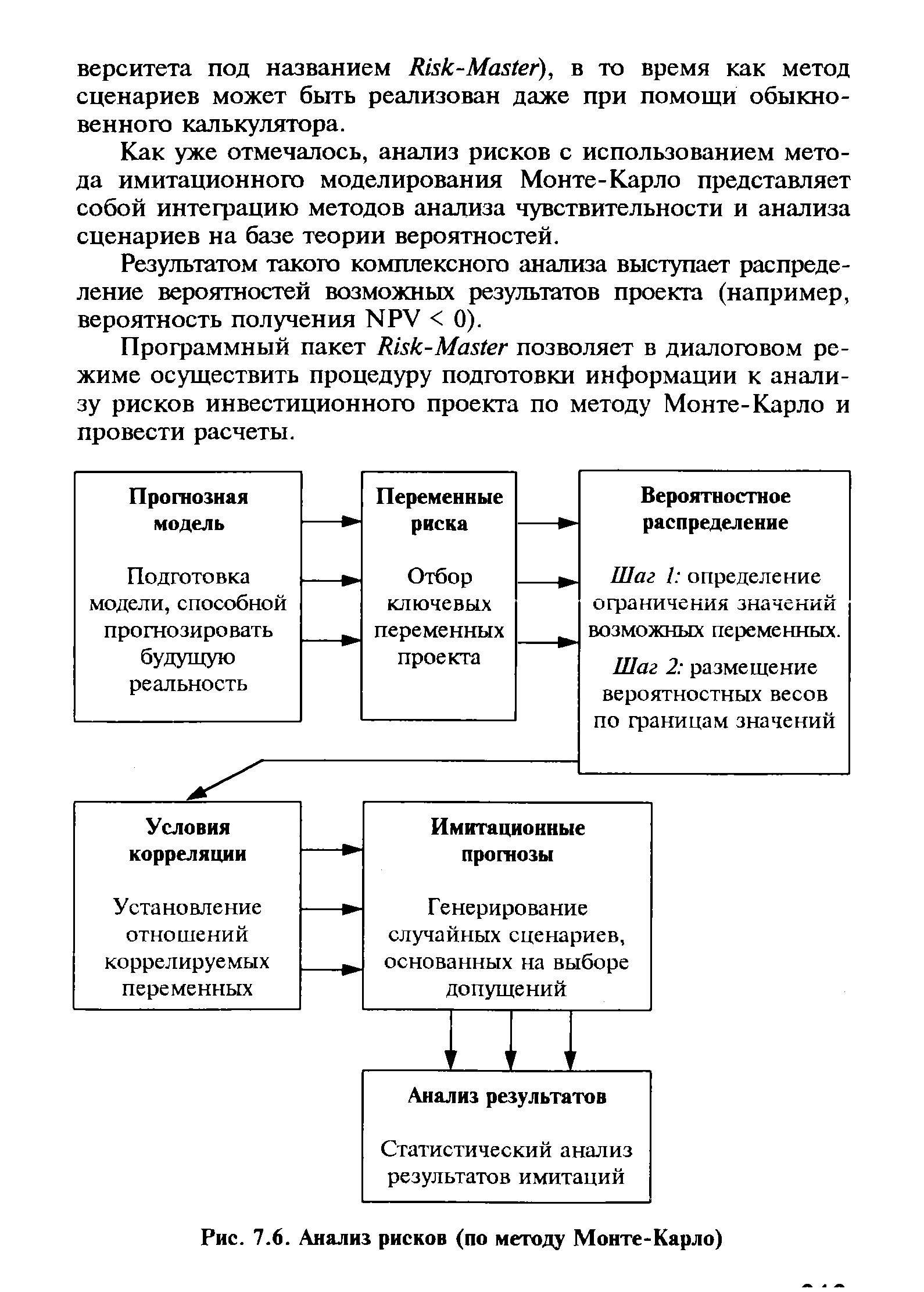 |
Каковы основы анализа рисков по методу Монте-Карло [c.255]
Алгоритм анализа графа с возвратом основан на использовании метода статистических испытаний и известного алгоритма Форда для сетевых графиков. Процедура Форда используется для расчета временных параметров отдельных фрагментов графа с учетом их топологии и задаваемых характеристик, а методами Монте-Карло имитируется реализация соответствующих дуг возврата. Таким образом, центральной процедурой алгоритма является моделирование событий контроля и согласования методом статистических испытаний. Исходы этих событий описываются вероятностями повторного исполнения определенных фрагментов проекта. [c.197]
Анализ единичного риска проекта начинается с установления неопределенности, присущей денежным потокам проекта, которое может основываться и на простом высказывании мнений, и на сложных экономических и статистических исследованиях с использованием компьютерных моделей. Наиболее часто используют следующие методы анализа 1) анализ чувствительности 2) анализ сценариев 3) имитационное моделирование методом Монте-Карло. [c.206]
Один из наиболее распространенных методов См. —метод Монте-Карло, который применяется лпя моделирования многих экономических процессов (в частности, работы складов, что позволяет определять оптимальные запасы), для анализа систем массового обслуживания и т.д. [c.345]
Фундаментальный анализ упущенных возможностей Углубленный анализ эффективности хозяйственной деятельности, сравнение с конкурентами и средним значением по рынку. Использование ых методов оценки (метод экспертных оценок, метод дерева решений, метод аналогий, анализ чувствительности и связанный с ним метод критических значений, анализ сценариев, метод Монте-Карло). Анализ эффективности диверсификации портфеля активов. Оценка влияния несистематических рисков. [c.75]
Метод Монте-Карло занимает видное место на небосводе анализа риска. В некоторых аспектах метод — квинтэссенция количественной оценки риска. Как многие новые математические инструменты, он изменил профессиональный язык анализа риска и принятые ранее способы оценки запасов нефти и газа. [c.165]
Анализу резервов нефти и газа методом Монте-Карло присущ один недостаток, вытекающий из определения доказанных запасов месторождения. В рамках современного общепринятого подхода низшая 10-я процентиль, или 1-я дециль, рассматривается как доказанная (Р), 50-я процентиль — как доказанная и вероятная (Р + Р), а верхняя 10-я процентиль (высшая дециль) — как доказанная вероятная и возможная (Р + Р + Р). В приведенном ранее примере различным уровням достоверности будут соответствовать такие показатели [c.172]
Проведение расчетных итераций является полностью компьютеризированной частью анализа рисков проекта методом Монте-Карло. 200-500 итераций обычно достаточно для хорошей репрезентативной выборки. В процессе каждой итерации происходит случайный выбор значений ключевых переменных из специфицированного интервала в соответствии с вероятностными распределениями и условиями корреляции. Затем рассчитываются и сохраняются результативные показатели (например, ЧДД). И так далее, от итерации к итерации. [c.12]
Далее проведем анализ методом имитационного моделирования Монте-Карло. В рассматриваемом примере исходим из предположения о независимости и равномерном распределении входных параметров [c.45]
На рис, 1.49 отражены результаты сравнительного анализа предложенного алгоритма и алгоритма попарной оптимизации подграфов A3. Изображена зависимость времени работы алгоритмов от р при ГА = В(8р, 1). Кривая 1 соответствует времени работы алгоритма попарной оптимизации, а кривая 2 — времени работы алгоритма Монте-Карло по достижении точности, достигнутой при реализации метода A3. Видно преимущество подхода, основанного на методе Монте-Карло, при решении больших задач распараллеливания. [c.155]
Технико-экономическое обоснование (ТЭО) Дерево решений . Проверка устойчивости. Определение точки безубыточности. Формализованное описание неопределенности и рисков. Анализ сценариев. Метод Монте-Карло [c.248]
Анализ риска по показателю ЧДД может быть выполнен одним из следующих трех методов 1) методом точечных оценок 2) методом дискретных вероятностей (дерева вероятных исходов) 3) методом моделирования распределений (Монте-Карло). [c.233]
Указанный тип уравнения — единственный, для которого может быть построен алгоритм нахождения оценок максимального правдоподобия и точечного прогноза (см. [16, 24 — 25]). Однако и для этого вида уравнений неприменимы методы ковариационного анализа (см. [16]), а экспериментальные оценки методом Монте-Карло в [24] привели к заключению о наибольшей пригодности двухшагового метода обобщенных наименьших квадратов. Но фактические вычисления [25] — правда, по более сложным типам моделей — не подтвердили в столь категорической форме этого вывода. С другой стороны, как следует из анализа аналогичной проблемы для регрессионных уравнений с текущими значениями переменных [16], двухшаговые процедуры даже в этом более простом случае не приводят хотя бы к асимптотическим оценкам наибольшего правдоподобия. [c.81]
Прежде чем мы начнем, мы должны разобраться с мифом о "случайных числах". Ни один генератор случайных чисел не производит истинные случайные числа. Вместо них алгоритм производит псевдослучайные числа - числа, которые являются статистически независимыми согласно большинству гауссовых признаков. Эти псевдослучайные числа фактически имеют длинный цикл, или память, после которого они начинают повторяться. Как правило, циклы достаточно длинны для того, чтобы повторение не обнаруживалось. Недавно, однако, было найдено, что псевдослучайные числа могут исказить результаты, когда большие количества данных используются в моделированиях по методу Монте-Карло. Обычно мы не сталкиваемся с этой проблемой в финансовой экономике. Однако многие из алгоритмов, используемых в качестве генераторов случайных чисел, являются версиями хаотических систем. R/S-анализ особенно хорошо справляется с раскрытием детерминированного хаоса и процессов с долговременной памятью. Поэтому чтобы гарантировать случайность наших испытаний, все ряды случайных чисел в этой книге перед использованием перемешиваются согласно двум другим рядам псевдослучайных чисел. Этот метод не устраняет всю зависимость, но сводит ее к фактически неизмеримым уровням, даже для R/S-анализа. [c.75]
Анализ чувствительности позволяет вам единовременно учитывать влияние изменения только одной переменной. Рассматривая проект при различных сценариях, вы можете выявить результаты ограниченного числа вероятных сочетаний переменных. Модель Монте-Карло позволяет рассмотреть все возможные комбинации. Использование модели при планировании долгосрочных вложений ассоциируется главным образом с Дэвидом Герцем и консалтинговой фирмой в области управления M Kinsey and ompany. Как мы увидим, этот метод является противоречивым. [c.241]
Система EXPRESS разработана для принятия управленческих решений и содержит стандартный набор функций финансового планирования и анализа, в том числе, функции по формированию прогнозных финансовых отчетов, бюджетированию, анализу, проектированию, анализу целей и консолидации данных. К специальным функциям системы относится, в частности, анализ рисков (в том числе, моделирование методом Монте-Карло). [c.326]
Программный пакет Risk-Master позволяет в диалоговом режиме осуществить процедуру подготовки информации к анализу рисков инвестиционного проекта по методу Монте-Карло и провести расчеты. [c.243]
К прямым относятся задачи определения эффективности операции, качества выбранного решения и i действия. Класс обратных составляют задачи оптимизации, определения оптимальных альтернат управляемых факторов, при которых критерий эффективности достигает экстремального минимального) значения. В чистом виде указанные классы задач встречаются нечасто, однако пр< имеют обратные задачи. Для решения прямых задач используются математико-статистические метод что исследуемые процессы в существенной мере подвержены воздействию неопределенных, случайнь полезности для ряда задач может быть оценена лишь вероятностно. Поэтому основой для анализа эс теория вероятности и ее модификации - теория массового обслуживания, теория марковских случай надежности, метод Монте-Карло (в частности для моделирования сложных ситуаций на ЭВМ). [c.106]
Метод Монте-Карло — метод формализованного описания риска, наиболее полно отражающий всю пшму неопределенностей, с которыми может столкнуться предприятие. В основе метода — анализ большого количества случайных сценариев. Его наименование происходит от города, где расположены многочисленные игорные заведения. На практике для расчетов по методу Монте-Карло используют специальные компьютерные программы. [c.225]
Монопсоническая власть (сила) 207 Монопсония 207 Монотонная функция 207 Монотонное преобразование 207 Монотонные функции полезности 380 Монте-Карло метод (метод статистических испытаний) 195 Морфологический анализ 207 Мощность аклератора 14 Мощность кода 146 Мультиколлинеарность 207 Мультимодальное распределение 202 Мультипликативная форма представления [c.475]
Фундаментальный анализ возможности (вероятности) возникновения кризиса Комплексный экономический анализ эффективности хозяйственной деятельности. Альтернативный анализ перспектив кризиса в отрасли с использованием элементов р-анализа (с использованием исторической р , технического анализа фондового рынка и т.д. Использование глобальных показателей вероятности банкротства (метод Бивера, метод Альтмана, модель Аа-рони-Джоиса-Свори и т.д.). Использование вероятностных методов оценки риска (метод экспертных оценок, метод дерева решений, метод аналогий, анализ чувствительности и связанный с ним метод критических значений, анализ сценариев, метод Монте-Карло). Анализ эффективности диверсификации портфеля активов. Оценка влияния несистематических рисков. Оценка бизнеса (операционный аспект). Оценка бизнеса (ликвидационный аспект). [c.74]
МОДЕЛЬ ИМИТАЦИОННАЯ (simulation model) — модель, предназначенная для анализа воздействия на к -л систему изменений в ее структуре и/или внеш условий функционирования (ретроспективный анализ или определение спектра допустимых сценариев будущего развития) При гаком подходе принадлежность модели к классу М и определяется не объектом моделирования, методами построения и структурой, а характером ее использования (используется для получения ответов на вопрос "Что, если ") См также Модегирование имитационное, Метод Монте-Карло [c.141]
Другая группа определений рассматривает исследование операций, исходя из различных методов, которые были разработаны специалистами по анализу операций, включая инвентарную теорию, линейное программирование, теорию очередностей, теорию игр, символическую логику и метод Монте Карло. Действительно,. исследование операций часто использует эти методы, однако оно также использует любые научные, математические или логические средства (включая диаграммы, схемы, карты, схемы потоков. и даже описательные словесные формулировки) для решения проблем, стоящих перед руководителем. Определять исследование операций исходя из применяемой техники является ошибкой, — говорят Миллер и Старр, — подобной определению медицины по набору медикаментов, которые врачи. применяют для лечения своих пациентов . [c.213]
Хсие (Hsieh, 1989) и Лебарон (LeBaron, 1990) выполнили моделирования BDS-статистики по методу Монте-Карло и нашли, что она устойчива по отношению к гауссовой нулевой гипотезе. Таким образом, подобно R/S-анализу, она может легко найти зависимость. Если линейная зависимость найдена, BDS-статистика является значимым тестом на нелинейность. К сожалению, она не может различать дробный шум и детерминированный хаос, но если ее использовать в сочетании с другими испытаниями, она представляет собой мощный инструмент. [c.238]
