Задача в таком случае сводится к построению линейной многофакторной модели [c.269]
Построение модели в таком случае будет сводиться на первом этапе к построению линейной многофакторной модели [c.70]
Регрессионные уравнения по каждой группе товарных нефтепродуктов имеют стандартный вид линейной многофакторной модели [c.122]
Линейные многофакторные модели [c.99]
Величины PJ, Р2,. . . , Рга называются факторами. Уравнение (14.7) называется линейной многофакторной моделью. [c.310]
В последние годы появился ряд работ, в которых описывается опыт применения многофакторных линейных корреляционных моделей в экономике нефтедобывающей промышленности. [c.63]
В многофакторных моделях используют линейное уравнение вида [c.322]
Корреляционная зависимость в отличие от функциональной является неполной, проявляется лишь в среднем и только в массе наблюдений. При корреляционной связи изменению аргумента соответствует несколько значений функций. В зависимости от количества отобранных факторов различают парные и многофакторные модели различного вида линейные, степенные, логарифмические. В практике прогнозирования наибольшее распространение получили линейные модели вида [c.129]
В экономическом анализе она представлена в виде многофакторных моделей линейных [c.31]
Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае линейной двухфакторной модели (25.75) считываются по формулам [c.567]
Выбор уравнения связи в многофакторных моделях задача сложная, поэтому предварительный качественный анализ характера связи каждого из п факторов с удельной фондоемкостью во многом определяет реальность получаемых результатов. При линейной или близкой к ней связи, применяется линейное уравнение множественной корреляции [c.524]
При наличии линейных форм связи для всех парных зависимостей возможно сделать вывод о линейности формы связи и для многофакторной модели. В том случае, если эти формы различны, то возможную форму связи можно установить путем перебора различных аналитических функций. Для этого необходимо рассчитать параметры корреляционных формул (см. ниже) при различных формах связи сравнить результаты выравнивания при принятых формах выбрать из них наилучшую форму связи. [c.120]
Рассмотрим теперь применение многофакторных моделей для прогнозирования воздействия некоторых факторов на такой показатель, как прибыль предприятия. На основе динамики показателей численности работающих на предприятии, объема выпускаемой продукции, затрат на природоохранные мероприятия и количества автомобилей в предприятии несложно построить регрессионную модель, позволяющую оценить значение прибыли. Опуская математические расчеты, которые следует проводить на ПЭВМ по специальным программам, для конкретных численных данных получаем следующую линейную многофакторную зависимость [c.131]
САРМ (рыночная модель) является однофакторной линейной регрессией. В случае рыночной модели предполагается, что имеется один фактор, влияющий на результирующую переменную, - доходность по индексу рынка. Таким же образом при расчете доходности могут использоваться многофакторные модели, в которых предполагается, что доходность ценной бумаги реагирует на изменения различных факторов. [c.32]
Одним из наиболее распространенных способов получения многофакторных прогнозов является упоминавшийся ранее классический метод наименьших квадратов и построение на его основе модели множественной регрессии [16]. Для линейного случая модель множественной регрессии записывается в виде [c.33]
Перед подробным рассмотрением собственно методики и практики применения ее в прогнозирования следует отметить, что в большинстве учебных пособий рассматриваются только линейные модели. Объясняется это, прежде всего, тем, что их достаточно просто исследовать, используя ручной счет или табличные процессоры. На основе простых моделей строится дальнейший прогноз. Однако, вручную рассчитать и провести исследование нелинейных многофакторных моделей, а тем более сделать на их основе прогноз почти невозможно, особенно если в модели учитываются более трех факторов. [c.97]
Поскольку для большого числа объединений не была установлена линейная зависимость между фактическим удельным расходом и приведенными выше факторами, то наряду с линейной моделью для всех объединений была опробована многофакторная степенная модель, которая описывается так называемой функцией Кобба— Дугласа ( 2 ) [c.52]
На развитых секторах рынка недвижимости эксперты-оценщики используют многофакторные линейные и нелинейные модели типа [c.287]
Можно также спрогнозировать величину расходов на просвещение и здравоохранение. Для этих целей используется многофакторная линейная модель [c.154]
Зависимости в экономике могут быть не только прямыми, но и обратными, и нелинейными. Регрессионная модель может быть построена при налички любой зависимости, однако в многофакторном анализе чаще всего используют линейные модели вида. [c.122]
Регрессионный анализ - один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, х[,х2,...,хп у должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида [c.101]
При использовании методов стохастического анализа сложных взаимосвязей уравнение регрессии по прибыли принимает вид линейного уравнения. Связь факторов с прибылью может быть представлена уравнением вида У=а+вх. На основании решения уравнения по каждому фактору, влияющему на прибыль, получается многофакторная корреляционная модель анализа прибыли [c.152]
В практике планирования и прогнозирования спроса достаточно часто применяются аналитические модели спроса и потребления, которые строятся в виде уравнений, характеризующих зависимость потребления товаров и услуг от тех или иных факторов. Другими словами, в аналитических моделях функциональная зависимость (25.68) принимает вполне определенный вид. Такие модели могут быть однофакторными и многофакторными. Рассмотрим аналитические модели спроса на примере линейных корреляционно-регрессионных статических моделей, используя конкретные данные обследования семей. [c.562]
Среди стохастических моделей наибольшее распространение получили линейные модели, реализуемые в рамках а) простого динамического анализа б) многофакторного регрессионного анализа в) анализа с помощью авторегрессионных зависимостей. [c.132]
Ввод информации и решение задачи на ЭВМ. В экономических исследованиях для многофакторных регрессионных моделей чаще всего приемлемы две формы связи факторов с функцией линейная и степенная. Для двухфакторных моделей применяются также гиперболическая и параболическая формы связи. [c.324]
Построение модели в таком случае сводится к построению линейной многофакторной модели lg //т э = Iga0 + af IgL + av lgvKOM + aN gN + + df lg/kg + а у lg V. Эта модель легко преобразуется в предыдущую, которая и используется.в последующем для установления норм расхода. [c.34]
Пусть имеется линейная многофакторная модель (14.7). Оценивая с помощью метода наименьших квадратов для уравнения (14.7) факторы Pi, 32,. .., Pm, составим сумму Рю% + Р2о%+ +Pm xm/> где р10, рао. .... pffl0— средняя квадратическая оценка случайных факторов, jfy, а/,. . . . . . , Kmj — значения непрерывных переменных х , х2,. . . , хт. [c.312]
Блок 6 — построение в каждом классе линейной многофакторной корреляционной модели, отражающей зависимость экономических показателей от объективных факторов производства (табл. 34). Корреляционно-регрессионный анализ предусматривается проводить с помощью модуля Ml08. [c.97]
| Рис. 1.8. Принципиальная схема алгоритма и программы машинного решения многофакторных линейных корреляционных моделей (блок-схема АИНФ) | 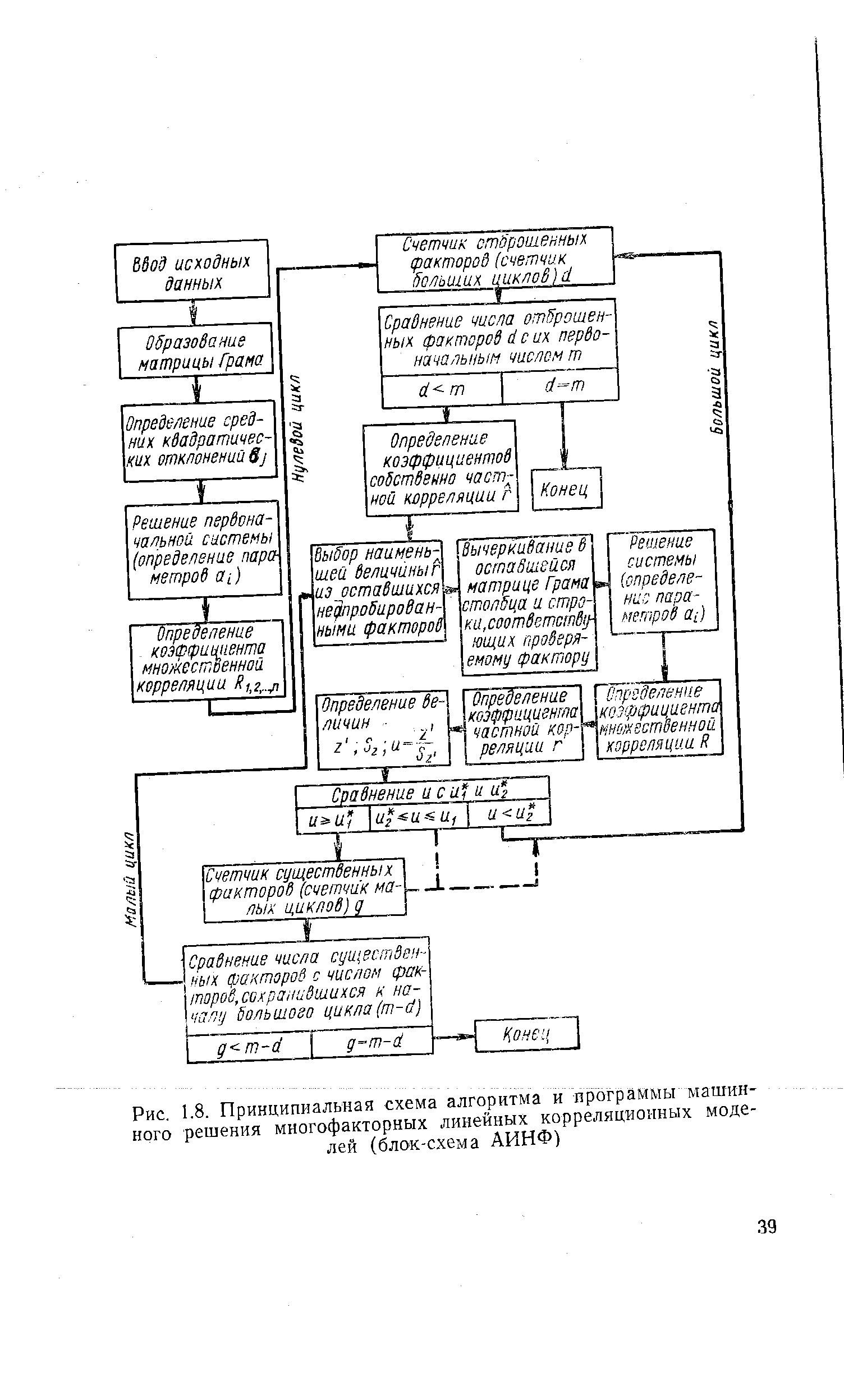 |
Причинно-следственное моделирование (многофакторные модели) нацелено на анализ достаточн двумя или более переменными. Например, при разработке прогноза объема спроса на швейные изде уровень доходов населения, взаимозаменяемость товаров, уровень цен, объем производства и другие ф Степенные, линейные многофакторные уравнения регрессии могут использоваться и при оп численности работников по той или иной управленческой функции и для решения множества других г [c.110]
Наиболее предпочтительны линейные многофакторные регрессионные модели. При использовании же нелинейных многофакторных моделей увеличение числа параметров ведет к снижению точности оценок и сложности интерпретации возникают сложности и при их оптимизации. Однако практически наиболее употребимые непрерывные (линейные и нелинейные) регрессионные модели предполагают наличие качественной однородности рассматриваемой совокупности, что наблюдается далеко не всегда. Неизбежны и различия в уровне техники, технологии и организации производства на отдельных объектах исследуемой совокупности, вызванные различиями в возрасте объектов (или отдельных единиц оборудования), их мощности, структуре выпуска продукции и ее назначении, природных условиях и т. д. Эти различия могут быть таковы, что внутри общей совокупности четко выделяются особые подсовокупности с различными характеристиками интересующих нас зависимостей. В этих условиях применение непрерывных моделей неправомерно, что вынуждает переходить к построению дискретных и дискретно-непрерывных моделей. [c.40]
Теперь, когда появилась некоторая ясность в вопросе кто "виноват" в бурном росте российского рынка акций, можно заняться вопросом который больше всего волнует всех инвесторов что делать дальше Для того чтобы ответить на этот вопрос, недостаточно знать основные факторы влияния. Кроме этого необходи-мооценить степень их влияния на динамику рынка акций. С этой целью мы построили многофакторную модель индекса РТС, используя аппарат множественной линейной регрессии. [c.75]
С учетом пяти форм полиномиальных уравнении тренда, можно получить девять форм уравнений регрессии. Речь идет только о трендах, т. е. об однофакторных моделях. (В Ex el, как известно, имеется также мощный инструментарий линейного многофакторного коррешвдионно-регресснонного моделирования.) [c.155]
Теснота связи между переменными величинами может иметь различные значения, если рассматривать ее с позиции характера зависимости (линейная, нелинейная). Если установлена слабая связь между переменными в линейной зависимости, то это совсем не означает, что такая связь должна быть в нелинейной зависимости. Показателем, хаРактеРизУющим значимость факторов при различной форме связи, яв/1яется корреляционное отношение. Оценка факторов по корреляционному отношению уже на этом этапе анализа позволяет предварительно уст0новить вид многофакторной связи, что служит хорошей предпосылкой ПРИ выборе конкретной модели исследуемого показателя. [c.17]
Построенные многофакторные корреляционные модели по нефте-х добывающей промышленности Украины, нефтегазодобывающим управлениям Прикарпатья, НГДУ Долинанефтегаз вида множественной линейной функции, мультипликативной функции Кобба — Дугласа, кинетической производственной функции позволили сделать количественную оценку влияния различных факторов в их взаимосвязи на динамику себестоимости добычи нефти и попутного газа. Исследована специфика экономико-математического моделирования в нефтедобывающей промышленности, и с этих позиций обосновано использование в качестве функции себестоимости добычи нефти и газа кинетической трансцендентной функции вида [c.111]
Рассмотрим теперь двухфакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х ) и размера семей (л ). Множестьенный (многофакторный) корреляционно-регрессивный анализ решает три задачи определяет форму связи результативного признака с факторными, выявляет тесноту этой связи и устанавливает влияние отдельных факторов. В нашем случае эта модель имеет вид [c.564]
Здесь текущее значение Y — функция от трех наиболее недавних предыдущих значений. Отсюда авторегрессионная модель — это модель, в которой моделируемые значения задаются линейной функцией от предыдущих наблюдений. Читатели здесь увидят сходство с автокорреляцией или внутрирядовой корреляцией, где существовала корреляция между остатками в уравнении регрессии. В действительности, если мы посмотрим на уравнение (7.7), то узнаем многофакторное уравнение регрессии, где прошлые значения У являются независимыми переменными [c.321]
Смотреть страницы где упоминается термин Линейные многофакторные модели
: [c.134] [c.2] [c.69] [c.124] [c.22] [c.25]Смотреть главы в:
Методы прогнозирования в условиях рынка -> Линейные многофакторные модели
