| Рис. 7.4. График вероятностного ряда биномиального распределения | 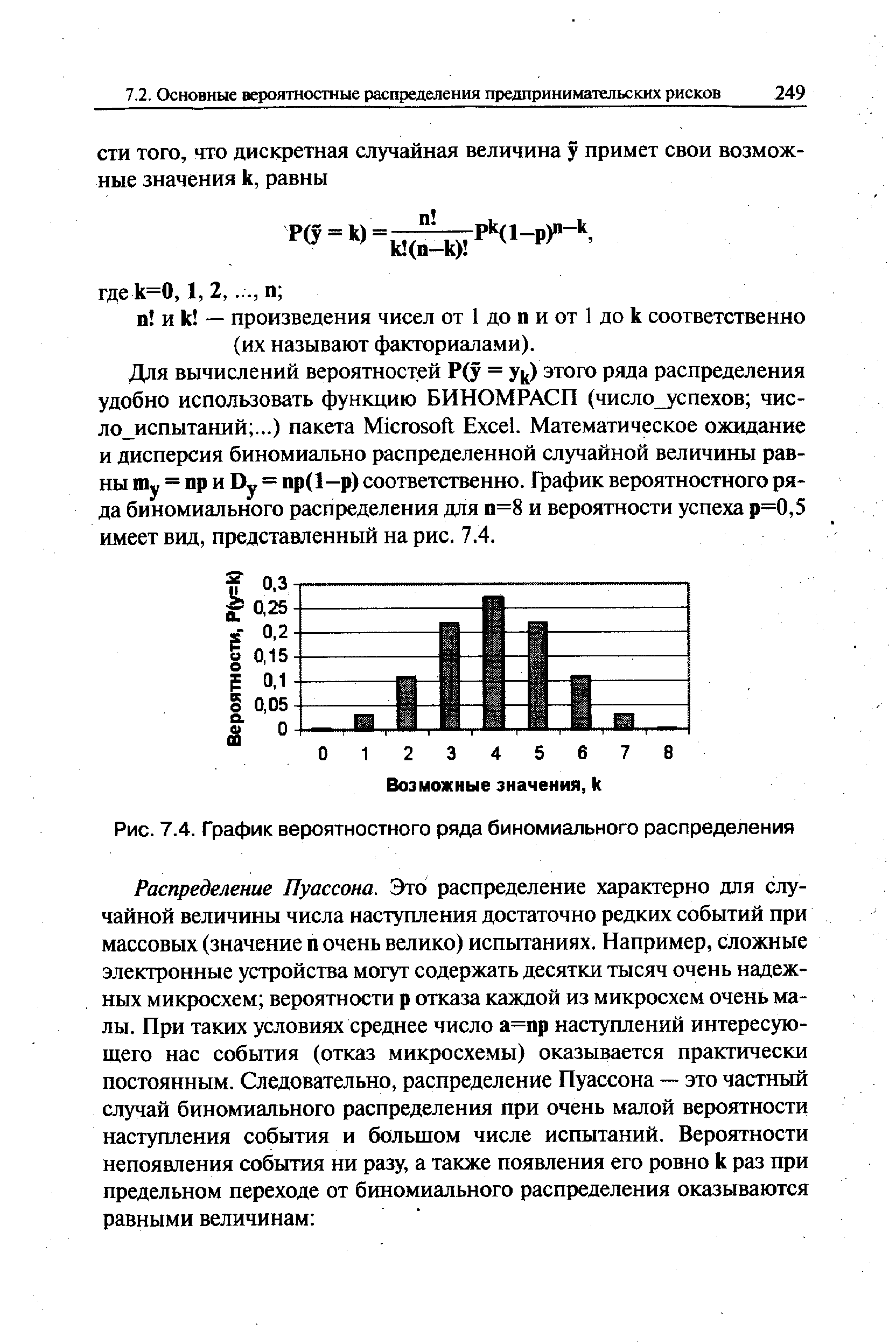 |
Биномиальный метод предполагает, что срок до исполнения опциона может быть разделен на ряд периодов, в каждом из которых возможны только два изменения цены. В предыдущей главе мы оценивали стоимость опциона только с одним периодом до исполнения. Преимущество разделения срока жизни опциона на множество подпериодов состоит в том, что это позволяет вам понять, что стоимость активов может иметь множество будущих значений. Вы можете рассматривать формулу Блэка-Шольца как быстрый способ решения, когда ряд таких подпериодов бесконечен, а следовательно, не ограничено и число будущих возможных цен актива. [c.578]
Эта глава начинается с рассмотрения механизма заключения и исполнения опционных контрактов и того, как их можно использовать для создания различных схем денежных платежей на базе рискованных активов, лежащих в основе опционов. Далее мы используем закон единой цены для получения уравнений, увязывающих между собой цены опционов "колл", опционов "пут", акций и облигаций, а также рассмотрим биномиальную модель оценки стоимости опционов и модель Блэка—Шоулза. Затем будет показано, как по аналогии с опционами можно провести оценку стоимости облигаций и акций корпораций, воспользовавшись той же терминологией. В конце главы приведен обзор ряда приложений, для которых применима методика оценки условных требований. [c.260]
М (т) = пр а2 (т) — npq. Биномиальное распределение имеет место при ряде неза- [c.21]
Последний ряд называется биномиальным. Если т — целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона. Действительно, т — п + 1 = 0 при п = т + 1. [c.138]
Основу организации статистического контроля качества составляет анализ закономерностей распределения отдельных значений признака в их обшей совокупности. Наиболее распространенным для многих признаков в производственной практике является нормальное распределение. На примере этого распределения автор показывает те задачи, которые должны решаться в процессе обеспечения качества. Кроме этого распределения, автор раскрывает возможности для практической организации контроля качества и выявления дефектных изделий целого ряда других распределений — биномиального, распределения Пуассона и т. д. [c.239]
Указанные таблицы получены перестроением таблиц биномиального распределения накопленной вероятности и приведены в ряде источников [4, 20]. [c.89]
Параметрами рассмотренного метода сглаживания биномиально взвешенным скользящим полиномом являются k, задающий порядок полинома, и /, определяющий размер активной окрестности (т.е. число членов временного ряда вблизи заданного периода времени, на основе которых получается сглаженное значение ряда для данного периода времени). Следует использовать значения параметра k, равные О, 1 или 2. В первом случае сглаженный ряд локально тяготеет к константе (причем тем сильнее, чем выше значение Г), во втором случае - к прямой линии (поэтому в этих случаях допускается спрямление изгибов основной тенденции), а в третьем случае - к параболе. Выбор размера активной окрестности (сводящийся к выбору значения I) определяется теми тенденциями, исследование которых представляет интерес. Для исследования краткосрочных тенденций следует использовать малое значение /, а для исследования долгосрочных - большое. Выбор значения параметра / может быть произведен на основе анализа передаточных функций. [c.225]
Свойства метода сглаживания биномиально взвешенным скользящим полиномом, в том числе и вблизи краев временного ряда, исследованы в (Бессонов, 1993). Там же проведено и его сравнение с другими методами сглаживания. [c.225]
Сглаживанием исходного ряда методом биномиально взвешенного скользящего полинома с параметрами k и / получается первое приближение тренда (рис. Ш). [c.226]
В простейшей биномиальной модели из 13.1 определим с.в. Сп=тах(0,5п— SQ). Составьте ряды распределения для с.в. Сь С2, С3 [c.108]
Эта модель имеет ряд существенных недостатков, в числе которых и то, что в наш век сверхбыстрых коммуникаций может поступить больше одного сообщения в течение одной секунды. Можно улучшить эту модель, введя, скажем, полусекундные интервалы. Соответствующей биномиальной моделью будет бином с параметрами (120, 1/12). В этом случае вероятность получения 8 сообщений будет равна 0,1145 [c.206]
К настоящему времени разработан ряд моделей ценообразования опционов на срок их действия (до момента исполнения). Наиболее широко встречающаяся модель — это модель, разработанная Блэком и Сколсом (1973), которая использует непрерывные временные стохастические исчисления для нахождения стоимости, она будет рассмотрена в гл. 10. Наиболее известная дискретная временная модель — это биномиальная модель, разработанная Коксом и другими (1976), а также Рендельмэном и Бартером (1979). В последнее время также возрастает интерес к триномиальным моделям. В этом разделе мы обсудим биномиальные и триномиальные модели в приложении к ценообразованию опционов. [c.394]
Биномиальная модель допускает возможность создания безрискового портфеля посредством хеджирования длинной позиции по активу короткой позицией по ряду справедливо оцененных опционов по покупке этого актива. Следовательно, только безрисковая процентная ставка должна быть использована для дисконтирования, поскольку предполагается, что если портфель захеджиро-ван наилучшим образом, он будет безрисковым и, следовательно, должен характеризоваться безрисковой процентной ставкой. [c.395]
Изложенные ниже вопросы охватывают задачи обучения принятию решения, основные принципы которых те же, что и ранее, но форма обрабатываемых данных несколько иная. Если производится обследование какого-либо вида продукции, которую предполагается изготовить или закупить, отдельные единицы продукции могут быть классифицированы как годные или негодные, качественные или дефектные, приемлемые или неприемлемые. Обследование изделия выражается в одном из этих двух возможных сообщений, а данные, полученные из ряда таких наблюдений, могут быть представлены как число дефектных изделий г, обнаруженное при обследовании п изделий. Если вероятность оказаться дефектными одинакова для всех единиц продукции, то, как хорошо известно, вероятностное распределение величины г. будет биномиальным. Аналогично, изучая поведение потребителей при покупке товаров, можно всех потребителей классифицировать на покупателей и непокупателей того или иного вида товара. Задания могут выполняться успешно или неуспешно, рабочий может быть загружен или не загружен, машина может работать или простаивать. Все это примеры ситуаций, в которых основные данные имеют двоичный характер, и при подходящих предположениях исходный случайный процесс может в этих случаях моделироваться с помощью биномиального распределения. Задачи такого рода можно проиллюстрировать на примере из области контроля качества. [c.182]
А. Биномиальное распределение. Это распределение числа X появления события А в серии из я независимых испытаний. Вероятность наступления события А в каждом испытании равна р, а вероятность его отсутствия q = 1 - р. В каждом испытании возможны два исхода наступление или ненаступление события А. При сформулированных условиях ряд распределения числа появления события А определяется формулой Бернулли [c.24]
Каждая из 12 месячных подсерий (т.е. временных рядов, полученных из уровней январей всех лет, февралей и т.д.) ряда, полученного в предыдущем пункте, сглаживается методом биномиально взвешенного скользящего полинома с параметрами К и L. Совокупность полученных сглаженных подсерий дает первое приближение сезонной составляющей динамики исходного ряда (рис. ПЗ). [c.226]
В V.A.3 мы приведем ряд хорошо известных результатов для доверительных интервалов и критериев для среднего одной нормальной совокупности или разности между средними двух нормальных совокупностей. Мы обсудим, например, /-критерий для одной либо двух совокупностей с неизвестными и возможно различными дисперсиями. Рассматриваются предположения -критерия и имитационное моделирование, а также биномиальное распределение и оценивание квантилей. В V.A.4 изучается определение объема выборки. Для доверительного интервала заданной длины обсуждается двойная выборка и (асимптотически состоятельная и эффективная) последовательная выборка. Многочисленные применения в моделировании и экспериментах Монте-Карло показывают, что правила останова срабатывают. Мы также определим объем выборки для проверки гипотез с заданными ошибками аир при применении двойной выборочной процедуры. В качестве альтернативы можно взять подход, основанный на селекции ( зона безразличия ), который отбирает с заданной надежностью уточненную совокупность. Эвристический последовательный метод применен в имитационном эксперименте. Проверку гипотез с заданными ошибками а и р и строго последовательной выборкой можно осуществить по критерию последовательного отношения вероятностей Вальда (Wald) (КПОВ) (при условии, что нет мешающих параметров следовательно, для биномиальной совокупности существует точный КПОВ). Часть А заканчивается приложениями, упражнениями и библиографией. [c.121]
