Производственная функция 3 39, 43-50, 52, 53, 61-70, 74, 109, 110, 112, 225-229, 263 4 49 Кобба—Дугласа 3 229, 230 национального продукта 4 201, 202 Производственный оптимум 3 36 Производство (понятие) 1 47 3 26-29 Пространство благ 1 127, 128, 133 2 58, 70, 75, 244, 246-252, 254, 266 Процент(ы) [c.269]
Попробуем принять решение вместе с Робинзоном. Найдем сначала производственный оптимум. Для этого нам необходимо знать сложившееся на рынке соотношение цен на выпускаемые Робинзоном товары (мы предполагаем, что объем производства и потребления Робинзона слишком мал, чтобы повлиять на соотношение цен, и это соотношение задается Робинзону рынком). Если соотношение цен Рх/Ру известно, то задача нахождения производственного оптимума в нашей модели весьма проста. Нам необходимо построить семейство параллельных прямых линий с углом наклона -Рх/Ру- Каждая из этих линий (на графике аналогичных бюджетным линиям) будет представлять все множество наборов товаров, характеризующихся одинаковым уровнем дохода при [c.36]
| Рис. 3. Производственный оптимум Робинзона. | 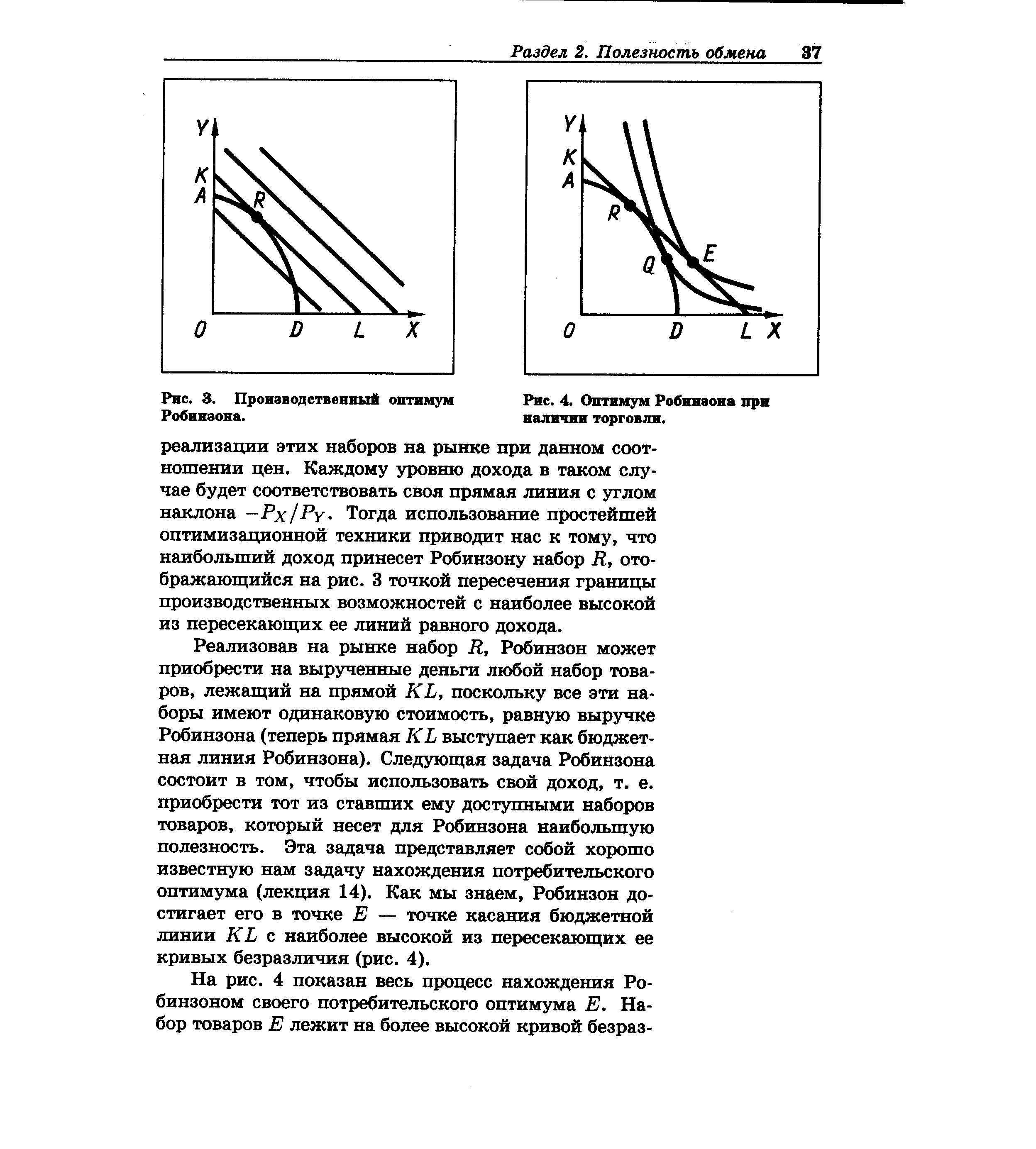 |
Задачи на отыскание оптимума решаются по сложным алгоритмам и связаны с многовариантностью расчетов и большим объемом вычислений. К подобного рода задачам относятся обоснование производственной программы предприятия с целевой функцией — минимизация затрат или максимизация прибыли, разработка оптимальной загрузки оборудования в условиях его технологической взаимозаменяемости с целью выпуска максимального количества продукции и др. Для решения задач различного класса сложности должны использоваться соответствующие вычислительные машины и другие технические средства. [c.401]
Формализованная постановка задачи нахождения оптимальной производственной программы предприятия найти план х, который удовлетворяет условиям (24.1) — (24.5), (24.7) и который соответствует оптимуму (максимум или минимум в зависимости от смысла) по критерию (24.6). [c.413]
Итак, для нахождения оптимальной производственной программы необходимо такое решение системы многих уравнений с многими неизвестными, при котором критерий (целевая функция) достигает оптимума. Система уравнений и неравенств (24.1) — (24.5), (24.7) обладает следующим свойством она линейна относительно неизвестных. Это означает, что неизвестные входят в уравнения, неравенства и критерий лишь в первой степени и что отсутствуют произведения неизвестных. Методом решения подобных задач, которые носят название задач линейного программирования, служит так называемый симплекс-метод. Симплекс-метод изложен в целом ряде книг. Ограничимся лишь его технико-экономической интерпретацией. [c.413]
Поскольку большинство производственно-технических и хозяйственных задач могут иметь несколько решений с переменными значениями затрат ресурсов или времени, то при составлении плана возникает необходимость его оптимизации, т.е. поиска варианта, обеспечивающего достижение поставленных целей при наименьших затратах ресурсов и времени. Это может быть достигнуто путем проведения многовариантных расчетов и обоснованного выбора из них оптимального варианта. Для этого пользуются методом вариантных постепенных приближений к оптимуму с помощью итерации, т.е. повторного применения счетных операций. Рассчитываемый вариант плана анализируют с точки зрения выявления [c.16]
Как следует из проведенных расчетов, фактическая загрузка производственных мощностей далека от оптимальной, производство осуществляется на уровне безубыточности, что является следствием политики, проводимой головным предприятием. Другим подтверждением объективности проведенных расчетов является то, что точка технологического оптимума (min АТС) достигается на уровне 3/4 от максимальной производительности, что соответствует известному техническим специалистам уровню наиболее рациональной загрузки машин и оборудования. Положительным моментом является тот [c.337]
Многовариантный анализ. Мы рассмотрели случай, когда надо выбрать один из двух вариантов при ограничении на один фактор производства. В реальности приходится сопоставлять несколько вариантов с учетом многочисленных ограничений. В этом случае для решения производственных проблем на основе изучения зависимости затраты — производство — прибыль следует использовать методы линейного программирования. В качестве оптимума может быть взят максимум прибыли до уплаты процентов и налогов либо минимум затрат С [c.105]
Оптимум величины партии обусловливается многими факторами временем переналадки станков, принятой системой организации производственного процесса, которая в значительной степени зависит от соотношения трудоемкости операций, длительности производственного цикла и пр. [c.246]
Из соотношений (1) и (2), в частности, следует, что в оптимуме предельные производительности производственных ресурсов gi пропорциональны их ценам. Кроме того, затраты на прирост единицы продукции Pi/gi равны множителю Лагранжа X,. Их называют при- [c.34]
Получаем те же условия (1), которые соответствуют минимуму затрат для заданного объема производства. Но в формуле (12) множитель Лагранжа заменен на цену продукции. В оптимуме цена должна быть равна предельным затратам и, следовательно, в долгосрочном периоде и для адаптированной структуры КПЗ = ДПЗ=р, т. е. краткосрочные и долгосрочные затраты равны между собой и одновременно равны цене продукции. Это важное свойство оптимума использовано при построении модели распределения затрат между разведкой и разработкой месторождений. В краткосрочном периоде независимо от того, оптимальна производственная мощность (т. е. достигнута структурная адаптация к выпуску продукции) или нет, цена всегда должна быть равна краткосрочным приростным затратам. [c.37]
Третья макроэкономическая цель — достижение народ-рым хозяйством состояния эффективности. Эта цель означает, что экономика страны должна функционировать с максимальной отдачей в виде совокупности созданных благ при достижении минимума народнохозяйственных издержек (при рациональном использовании ограниченных производственных ресурсов). Макроэкономическая эффективность, как правило, рассматривается на трех основных уровнях технологическом, экономическом и социальном. Достижение эффективности на каждом из уровней означает выполнение глобального макроэкономического оптимума (который в честь выдающегося экономиста, внесшего большой вклад в его понимание, называют оптимумом В. Парето). Проиллюстрируем это обстоятельство с использованием метода кривой производственных возможностей (КПВ) макроэкономики. [c.34]
Согласно принципу оптимума, эффективная точка производства товаров А и Б, с учетом торговли, будет определяться точкой касания линии мировых цен СС и кривой производственных возможностей АА. Ца рис. 9.1 — это точка F. Данная точка определяет, что выгоды от экспорта товара А становятся максимальными, а сам экспорт равен разности (Хр — Хе). Точка Хе характеризует внутреннее потребление товара А, импорт же товара Б составит разность (Ye — Следовательно, координаты точки G, полученные в- итоге, означают, что за счет внешней торговли [c.266]
Обоснована структура задач оптимизации ресурсов производственного подразделения. Предложены методы практических расчетов и таблицы, основанные на теории массового обслуживания, имитации на ЭВМ, методах поиска оптимума. [c.361]
Информация о наличии альтернативных оптимумов дает возможность выбора альтернативного варианта, в наибольшей степени отвечающего сложившейся производственной ситуации. [c.455]
Многие небольшие и растущие фирмы, следуя настоятельным требованиям рынка, расширяют свои производственные мощности, мало заботясь о перспективной эффективности этих мероприятий. Такие предприя тия, растущие как грибы, в большинстве случаев страдают дублированием и малой производительностью, хотя и работают рентабельно. Однако на хорошем рынке очень быстро появляются конкуренты. В конце концов прибыли зависят от эффективности производства, от оптимальных производственных систем. Только постоянная забота, направленная на поддержание систем в состоянии оптимума, может, предотвратить неизбежность проведения срочных программ по снижению издержек, чтобы выстоять в конкурентной борьбе. [c.413]
Пятое условие предполагает, что при сложившихся параметрах производства обеспечивается гармоничное сочетание локальных оптимумов в данной альтернативной производственной ситуации. Процедуры выработки команды-распоряжения, связанного с упрочением достижений трудовых коллективов, должны обязательно базироваться на автоматизированных оперативных расчетах по экономическому анализу хода внедрения плановых и внеплановых организационно-технических мероприятий по повышению экономической эффективности производства. [c.151]
Первая область оптимизации является наиболее благоприятной для согласования локального и глобального оптимумов, т. е. для применения экономико-математического моделирования при решении задач по закреплению достижений трудовых коллективов. Примером подобных расчетов является, в частности, решение задач по предотвращению негативных последствий экономии материальных и трудовых ресурсов посредством отыскания оптимального варианта наилучшего использования их высвобождения, в том числе посредством пересмотра действующих норм создания условий для интенсификации усилий трудовых коллективов по перевыполнению производственных заданий на базе увеличения частоты отгрузки отдельных видов продукции плановым потребителям во избежание переполнения складов расчета экономии по транспортным расходам вследствие повышения концентрации основного вещества, чистоты или других свойств готовой продукции, сокращающих объем непроизводительных перевозок, и т. д. [c.156]
Нормативное хозяйство используют на химических пред-- приятиях в двух главных направлениях в расчетах по конкретизации внутригодовых заданий снижения себестоимости продукции и ускорения оборачиваемости производственных запасов при решении задач по увеличению масштабов экономического маневра хозяйственными ресурсами в целях улучшения конечных результатов работы трудовых коллективов. При эксплуатации АСУП или ГВС эффект от предварительного решения на оптимум распределительных и перераспределительных задач по мобилизации и реализации внутрипроизводственных резервов в короткие сроки перекрывает затраты на организацию и использование в управлении текущего нормативного хозяйства. [c.205]
В настоящей работе сделана попытка определения зависимости оптимальной нормы производственного накопления от ряда факторов и изучения свойств оптимума. Некоторое внимание уделяется проблеме управления пропорциями между накоплением и потреблением в связи с динамикой материально-вещественной структуры общественного продукта. [c.5]
В защиту критерия максимума фонда потребления при решении задачи оптимизации нормы накопления выступает А. Ноткин, работы которого будут подробнее рассмотрены ниже. А. Ноткин, в частности, пишет ...оптимум производственного накопления и потребления... должен обеспечивать за определенный срок не только возможно большие приросты продукта, но и максимизацию фонда потребления 2. [c.33]
Однако и метод изучения свойства оптимума с помощью числовых моделей, взятых в отдельности, имеет права гражданства. Именно этот метод использует в вышеупомянутой работе А. Ноткин. Рассмотрим его особенности. Уже говорилось о том, что в основу построения модели положен коэффициент накопления, представляющий собой отношение нормы производственного накопления к темпу роста национального дохода. Так, если производственное накопление составляет 18% национального дохода, а темп роста национального дохода равен 9%, величина этого коэффициента рав- [c.38]
Следует заметить, что при всех очевидных достоинствах числовые модели А. Ноткина имеют ряд недостатков. Наиболее существенный из них связан с общими недостатками числовых моделей и заключается в том, что абсолютная величина оптимума для условий данной модели не вычисляется да и не может практически быть вычислена, поскольку такой расчет потребует перебора всех возможных вариантов экономического роста в пределах интервала допустимых значений нормы производственного накопления. Оптимальна ли 25% норма накопления, наилучшая из трех, предлагаемых автором . Трудно сказать. Три-четыре варианта могут дать некоторое понятие о свойствах оптимума, по не о его величине. [c.42]
Совершенно очевидно, что вычисление оптимальной нормы производственного накопления q требует знания функции А / ( У). т- е- зависимости индекса роста фонда потребления за >t лет от величины нормы производственного накопления. Если эта функция известна, величина оптимума определяется уравнением [c.48]
Тот факт, что норма производственного накопления изменяется в границах определенного интервала, создает при вычислении оптимума до- [c.48]
Пример 1. Эффективность капитальных вложений Е равна 0,5, плановый промежуток времени равен 5 годам, базисная норма производственного накопления составляет 10%. Линия I рис. 4 есть график роста фонда потребления при условии, что 0,10 <<7< 0,30. Ясно видно, что относительный (локальный) экстремум функции находится правее верхней границы (0,30). Расчет по формуле подтверждает это. Формула (2.7) дает следующее значение оптимума [c.58]
Предположим теперь, что Робинзон открыт обществом, имеет возможность продавать свою продукцию, а на вырученные деньги покупать необходимые ему товары. Как изменится оптимум Робинзона в этом случае Для ответа на такой вопрос нам уже недостаточно знать только множество производственных возможностей Робинзона и его систему предпочтений, так как Робинзон будет, вероятно, действовать по двухходовой схеме сначала определит свой производственный оптимум (т. е. набор товаров, позволяющий ему получить максимальный доход при реализации этого набора на рынке), а затем будет искать потребительский оптимум (т. е. самый предпочтительный из наборов товаров, доступных ему, исходя из полученного дохода). [c.36]
По аналогии с анализом, приведенным в предыдущем разделе, мы можем сделать вывод о том, что ставка заимствования будет приводить к правильным решениям (касающимся выбора производственных инвестиций при пренебрежении вопросом финансирования) при использовании правила сегодняшней ценности или правила внутренней нормы дохода тогда, когда оптимум расположен в зоне I. Аналогичным образом ставка кредитования будет приводить к правильным инвестиционным решениям, если оптимум находится в зоне III. Однако если оптимум расположен в зоне II, ни одна из этих ставок не годится для его конкретного определения. В таком случае правильные результаты даст некая ставка, которая (по величине) находится между ставками кредитования и заимствования. Иными словами, мы могли бы охарактеризовать эту правильную ставку дисконта как предельную норму производственных возможностей,11 которая в равновесии будет равна предельной норме субъективных временных предпочтений. В данной ситуации ни одно из правил не подходит для нахождения производственного оптимума без использования изо-квант полезности однако все, что здесь необходимо знать, — это информация о наклонах изоквант и границах производственных возможностей. Конечно, даже когда рассматриваемые правила удовлетворительны, они все равно вводят в заблуж- [c.190]
Среди положений кибернетики обособленное место занимает эмерджентность, т. е. свойство сложной системы обладать чертами, признаками и свойствами, не присущими ни одному из элементов этой системы в отдельности или присущими им не в одинаковых размерах. В частности, свойство эмерджентности выражается в несовпадении локального и глобального оптимумов. Например, ритмичность сборки и выпуска изделий заводом требует часто такой поставки комплектующих деталей и узлов, которая вызывает неритмичную работу отдельных цехов и производственных участков. Наоборот, организация строго ритмичной работы всех производственных звеньев предприятия при равномерной затрате труда может быть причиной неритмичных выпуска и сдачи продукции на реализацию. [c.303]
Все экономические науки прежде всего в тех или иных специфических формах, способах анализа, показателях, и моделях изучают экономические потребности людей. Не является исключением и макроэкономика. Она изучает совокупные (народнохозяйственные) экономические потребности, складывающиеся в той или иной стране в результате массовых взаимодействий фирм и домохозяйств, производителей и потребителей, государственного и негосударственного секторов, производственной и непроизводственной сфер, товарного, денежного и факторного внутреннего и внешнего рынков. Макроэкономические потребности выражают фундаментальные противоречия (формулируемые как проблемы народного хозяйства), анализ и поиск способов разрешения которых является основанием для обеспечения различных форм прогресса общества (экономический прогресс в данном случае рассматривается как условие технологического, социального и политического прогресса). В идеале (как желаемом состоянии) удовлетворение макроэкономических потребностей должно способствовать такому разрешению народнохозяйственных проблем, чтобы сосуществование естественной (данной самой природой) и искусственной (созданной человеком) среды жизнедеятельности людей качественно и количественно (в разумных условиях достаточности) повышало меру развития общества. С позиции оптимума хозяйственного развития это должно означать, что при соблюдении ограничения NEV= onst максимизируется следующая целевая функция [c.5]
Вывод, который сам Г. Госсен сформулировал так "Лицо максимизирует свою полезность, когда распределяет имеющиеся у него денежные средства между различными благами так, что достигает равного удовлетворения от последней единицы денег, истраченной на каждый из товаров" 3. Впоследствии это положение воплотилось в известном правиле предельного анализа экономики о равенстве предельной нормы замещения конкурирующих благ и производственных факторов для получения макси-мальноторезультата (оптимума). [c.65]
Очевидно, в этой схеме реализуется фундаментальное положение теории оптимального планирования план, цены и показатели стимулирования хозяйственной деятельности должны быть взаимоувязаны и получаться из единого решения производственной задачи на оптимум. Таким образом, на стадии планирования закладываются экономические условия для выполнения оптимального плана, а также стимулируется выявления новых производственных возможностей. [c.189]
Разработчики системы Toyota выделяют четыре этапа приближения структуры фирмы к оптимуму. П е р вый этап — технологическая форма специализации производственных звеньев. Характеризуется универсальностью и вместе с тем сложными технологическими маршрутами, большими транспортными издержками, длительным временем переналадки оборудования, большими затратами на заработную плату высококвалифицированных рабочих. На этом уровне система ЛТ не внедряется. Технологическая форма специализации используется при выполнении предприятием разовых или мелких повторяющихся заказов. [c.452]
Такое противопоставление встречается, например, в работе К- К. Вальтуха по проблеме оптимума накопления1. Критика автором различных критериев оптимальности представляет значительный интерес. Рассмотрим некоторые аргументы К. Вальтуха, направленные против максимума фонда потребления как критерия оптимизации нормы производственного накопления. [c.27]
Аппарат, используемый А. Ноткиным, — числовые модели роста национального дохода и фонда потребления в зависимости от нормы Производственного накопления. Здесь сразу же следует поставить вопрос возможно ли статистическое изучение Конечно, данные о динамике нормы производственного накопления за ряд лет (аналогичные приведенным выше) позволяют сделать определенные выводы о политике капитальных вложений за весь период экономического развития нашей страны и с этой точки зрения весьма полезны. Однако они не могут ответить на вопрос, насколько величина нормы накопления данного года приближается к оптимальной. Не поможет и коррелирование фонда потребления от нормы производственного накопления, которое, вообще говоря, возможно (поскольку для каждого года экономического развития можно выявить точку корреляционного поля), но методологически неверно, ибо условия различных лет несопоставимы (разная производительность общественного труда, разная фондоемкость продукции, различно число занятых в процессе материального производства и т. д.). Естественно, что для каждого отдельного года существует лишь одна норма производственного накопления. Итак, на вопрос о возможности статистического изучения оптимума накопления и потребления для данного периода следует ответить отрицательно. Остаются два пути числовое моделирование и математическое моделирование. [c.37]
Ограничения, налагаемые на величину нормы производственного накопления, значительно усложняют поиски оптимума. В частности, формула относительного экстремума (2.7) действует теперь только в одном случае, представленном на рис. 3 в случае, когда, относительный (локальный) максимум функции (2.6) находится внутри интервала изме 1ений q. Однако могут быть и случаи (отвечающие реальным экономическим условиям, о которых речь ниже), когда относительный (локальный) максимум не попадает в заданный интервал. Рассмотрим 2 примера. [c.58]
