Резюмируя этот раздел, мы приходим к выводу, что эффективность функционирования выше всего у компаний, производящих продукцию, связанную технологией и сбытом (RMT). Очевидно, что одним из факторов успеха диверсификации является синергия. Компания, выпускающая несвязанную продукцию, имеет наименьшую рентабельность. Во-вторых, на рентабельность и темп роста компании оказывают влияние темп роста отрасли и доля компании на рынке. Это подтверждается множественным регрессионным анализом. Этот принцип по-иному формулируется исходя из модели B G, в которой наивысшую эффективность имеет продукт типа корова . Наши выводы показывают, что наибольшей эффективностью продукты типа звезда (рис. 4.4). Мы также что если продукт модифицируется, то [c.138]
Целесообразно применять метод главных компонент совместно с методами статистического анализа, например, в множественном регрессионном анализе вместо большого набора независимых переменных xi, X2,. .., хт можно рассмотреть гораздо меньший набор главных компонент, к тому не коррелирующих друг с [c.185]
Для определения характера и степени влияния показателей монтажной технологичности на экономические показатели используется метод регрессионного анализа, позволяющий оценить монтажную технологичность путем соизмерения показателей технологичности и экономических показателей в уравнениях множественной регрессии вида [c.220]
В результате проведенного множественного регрессионного анализа получено уравнение [c.73]
Также можно воспользоваться множественной регрессионной моделью, которая учитывает влияние на изменчивость затрат нескольких факторов, так что формула совокупных затрат, приведенная выше, у = а + Ьх теперь примет следующий вид [c.123]
В большинстве случаев методы оценки исходят из допущения единственности фактора изменения затрат, хотя в действительности это далеко не всегда так. Множественный регрессионный анализ позволяет учитывать действие неограниченного количества факторов. [c.143]
Построение уравнения множественной регрессии по динамическим рядам является одной из важных проблем регрессионного анализа. Этот вопрос весьма актуален, но имеет дискуссионный характер. [c.71]
В случае нелинейности связи и при изучении множественной корреляции задача определения тесноты связи соотносится с проблемой изучения аналитической формы связи (коэффициент или отношение корреляции в этом случае прямо зависит от выбранной формы связи). Выявление аналитической формы связи означает моделирование хозяйственного процесса путем выявления закономерностей формирования значений результативного показателя под влиянием факторных показателей. Это основная и самая сложная задача в экономическом анализе, которая при стохастическом подходе решается методом регрессионного анализа. [c.114]
Большую роль в изучении влияния факторов на уровень среднечасовой выработки играют приемы корреляционно-регрессионного анализа. В многофакторную корреляционную модель среднечасовой выработки можно включить следующие факторы фондовооруженность или энерговооруженность труда процент рабочих, имеющих высшую квалификацию или средний тарифный разряд рабочих, средний срок службы оборудования, долю прогрессивного оборудования в общей его стоимости и т.д. Коэффициенты уравнения множественной регрессии показывают, на сколько рублей изменяется среднечасовая выработка при изменении каждого факторного показателя на единицу в абсолютном выражении. Для того чтобы узнать, как за счет этих факторов изменилась среднегодовая выработка рабочих, необходимо полученные приросты среднечасовой выработки умножить на фактическое количество отработанных человеко-часов одним рабочим [c.392]
Для изучения влияния одних процентных ставок на другие целесообразно проводить корреляционно-регрессионный анализ, позволяющий измерить тесноту связи между изучаемыми показателями (корреляционный анализ) и определить теоретическую форму связи между ними (регрессионный анализ). Прежде всего необходимо получить подтверждение о том, что связь между двумя или более изучаемыми показателями существует, а затем измерить ее. Применение тех или иных методов корреляционного анализа зависит от целей исследования. В случае парной корреляции, т.е. когда анализу подвергается влияние одного показателя (фактора, х) на другой (результат, у), чаще всего используют линейный коэффициент корреляции. В случае множественной корреляции, т.е. когда проводят анализ влияния нескольких факторов (л , х . ... л ) на результат (у), как правило, рассчитывают парные, частные и совокупный коэффициенты корреляции. [c.622]
После проведения корреляционного анализа принимается решение о целесообразности построения уравнения регрессии, с помощью которого определяется аналитическое выражение формы связи между отдельными видами процентных ставок. С помощью регрессионного анализа выявляется изменение одной величины (результата) под влиянием одного или нескольких факторов, а множество прочих причин, оказывающих влияние на результат, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной) и многофакторной (множественной). Подбор аналитических функций (линейных и криволинейных) для построения уравнения регрессии осуществляется аналогично подбору функций для уравнения тренда. На практике теоретическая форма связи определяется с использованием пакета статистических программ на ПЭВМ. Для наглядного изображения теоретической формы связи значения показателей, полученные с помощью уравнения регрессии, наносят на график и сравнивают их с эмпирическими данными. [c.624]
Проблемы множественного корреляционно-регрессионного анализа и моделирования подробно изучаются в специальном курсе того же названия. В курсе Общая теория статистики рассматриваются только самые общие вопросы этой сложной проблемы и дается начальное представление о методике построения уравнения множественной регрессии и показателей связи. Рассмотрим линейную [c.268]
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой, или результативным признаком) обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной) и многофакторной (множественной). [c.113]
Проблема отбора факторных признаков для построения моделей взаимосвязи может быть решена с помощью эвристических или многомерных статистических методов анализа. Наиболее приемлемым методом отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ). Сущность данного метода заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. Факторы поочередно вводятся в уравнение так называемым прямым методом . При проверке значимости введенного фактора определяется, насколько уменьшается сумма квадратов остатков и увеличивается величина множественного коэффициента корреляции (R). Одновременно используется и обратный метод, т.е. исключение факторов, ставших незначимыми на основе -крите-рия Стьюдента. Фактор является незначимым, если его включение в уравнение регрессии только изменяет значение коэффициентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения. Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а коэффициент регрессии не изменяется (или меняется несущественно), то данный признак существен и его включение в уравнение регрессии необходимо. [c.118]
Множественный коэффициент детерминации С/ 2), представляющий собой множественный коэффициент корреляции в квадрате, показывает, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель. [c.122]
Множественный регрессионный анализ [c.82]
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной Y от нескольких объясняющих переменных Х, Х ,..., Х . Эта задача решается с помощью множественного регрессионного анализа. [c.82]
Для решения матричного уравнения (4.5) относительно вектора оценок параметров Ь необходимо ввести еще одну предпосылку 6 (см. с. 61) для множественного регрессионного анализа матрица Х Х является неособенной, т. е. ее определитель не равен нулю. Следовательно, ранг матрицы X X равен ее порядку, т.е. г(Х Х)=р+. Из матричной алгебры известно (см. 11.4), что г(Х Х)=г(Х), значит, г(Х)=р+, т. е. ранг матрицы плана X равен числу ее столбцов. Это позволяет сформулировать предпосылку 6 множественного регрессионного анализа в следующем виде [c.86]
Теорема Гаусса— Маркова, рассмотренная выше для парной регрессионной модели, оказывается верной и в общем виде для модели (4.2) множественной регрессии [c.87]
Добавление в регрессионную модель новой объясняющей переменной АЗ изменило коэффициент регрессии Ь (У по Х ) с 1,016 для парной регрессии (см. пример 3.1) до 0,854 — для множественной регрессии. В этом никакого противоречия нет, так как во втором случае коэффициент регрессии позволяет оценить прирост зависимой переменной Y при изменении на единицу объясняющей переменной Х в чистом виде, независимо от Х . В случае парной регрессии Ъ учитывает воздействие на Y не только переменной Х, но и косвенно корреляционно связанной с ней переменной Х . [c.90]
Как и в случае парной регрессионной модели (см 3.6), в модели множественной регрессии общая вариация Q — сумма квадратов отклонений зависимой переменной от средней (3.41) может быть разложена на две составляющие [c.102]
Уравнение множественной регрессии значимо (иначе — гипотеза Щ о равенстве нулю параметров регрессионной модели, т. е. Яо Pi = 02 — Рр= О, отвергается), если (учитывая (3.43) при т = р + 1) [c.103]
В предыдущих главах была изучена классическая линейная модель регрессии, приведена оценка параметров модели и проверка статистических гипотез о регрессии. Однако мы не касались некоторых проблем, связанных с практическим использованием модели множественной регрессии. К их числу относятся мультиколлинеарность, ее причины и методы устранения использование фиктивных переменных при включении в регрессионную модель качественных объясняющих переменных, линеаризация модели, вопросы частной корреляции между переменными. Изучению указанных проблем посвящена данная глава. [c.108]
Решение. По формуле (4.8) найдем вектор оценок параметров регрессионной модели b =(3,515 —0,006 15,542 60,110 4,475 —2,932), так что в соответствии с (4.9) выборочной уравнение множественной регрессии имеет вид [c.113]
При моделировании реальных экономических процессов мы нередко сталкиваемся с ситуациями, в которых условия классической линейной модели регрессии оказываются нарушенными. В частности, могут не выполняться предпосылки 3 и 4 регрессионного анализа (см. (3.24) и (3.25)) о том, что случайные возмущения (ошибки) модели имеют постоянную дисперсию и не коррелированы между собой. Для линейной множественной модели эти предпосылки означают (см. 4.2), что ковариационная матрица вектора возмущений (ошибок) е имеет вид [c.150]
Регрессионный анализ является популярным способом оценки функции затрат. Для простой регрессии используется одна независимая переменная, например, DLH или часы работы оборудования (последний показатель подробно обсуждается в Главе 16). Множественная регрессия определяется с помощью задания двух и более переменных, описывающих активность. [c.92]
Регрессионный анализ - это статистическая процедура для математической усредненной оценки функциональной зависимости между зависимой переменной и независимой переменной (независимыми переменными). Простая регрессия рассматривает одну независимую переменную цену или затраты на рекламу в функции спроса, а множественная регрессия рассматривает две или большее количество переменных, например, цену и затраты на рекламу совместно. В этой главе обсуждается простая (линейная) регрессия, например, Y = а + ЬХ и показывается, как метод наименьших квадратов применяется для расчета коэффициентов регрессии. [c.257]
Регрессионный анализ для случая одной независимой переменной. Например, спрос на автомобили как функция цены. См. Множественная регрессия и Регрессионный анализ. [c.469]
Регрессионный анализ представляет собой статистическую процедуру для математического расчета среднего соотношения зависимой и независимой переменных. Выделяют два вида регрессии простая регрессия и множественная регрессия. Простая регрессия включает одну независимую переменную, множественная — две и более. [c.118]
Ml 08. Множественный корреляционно-регрессионный анализ [c.35]
При регрессионном анализе экономических явлений важно решить вопрос о том, можно ли. полученное уравнение множественной регрессии использовать для планирования. Об этом можно судить по коэффициенту вариации, который показывает относительное отклонение теоретических оценок уровня торгово-управленческих расходов, рассчитанных по уравнению множественной регрессии, от фактических. В нашем случае коэффициент вариации составляет для I группы управлений—12,5%, для II группы —10,6% и для III группы — 17,5%. [c.184]
Регрессионный анализ (regression analysis) — статистическая модель для измерения среднего значения изменения независимой переменной в зависимости от изменения одной (простая корреляция) или нескольких (множественная корреляция) зависимых переменных. [c.239]
Такого рода характеристика явлений, влияющих на уровень и динамику валютного курса, является непременным этапом, предшествующим самостоятельному статистическому анализу факторов на основе конкретного цифрового материала. Дальнейший анализ выглядит чаще как моделирование взаимосвязей и оценка тесноты взаимозависимости (корреляционно-регрессионный анализ). Напомним, что выбор функции осуществляется исходя из показателей значимости уравнения и ошибок аппроксимации. Это относительная ошибка аппроксимации, средняя квадратическая ошибка аппроксимации (6ОСТ) (чем они меньше, тем лучше уравнение) и коэффициент множественной детерминации (R2) или коэффициент множественной корреляции (R) (чем ближе он к 1, тем более вероятность, что уравнение регрессии носит совершенно случайный характер). Для проверки значимости используют F-критерий с распределением Фишера. [c.670]
Ниже, в 4.3, рассматривается ковариационная матрица вектора возмущений ]Г , являющаяся многомерным аналогом дисперсии одной переменной. Поэтому в новых терминах1 приведенные ранее (с. 61, 82 и здесь) предпосылки для множественного регрессионного анализа могут быть записаны следующим образом 2 [c.86]
Как уже отмечалось выше, равенство дисперсий возмущений (ошибок) регрессиии е/ (гомоскедастичность) является существенным условием линейной классической регрессионной модели множественной регрессии, записываемым в виде У е [c.155]
| Рис. 4. Блок-схема модуля М108 Множественный корреляционно-регрессионный анализ | 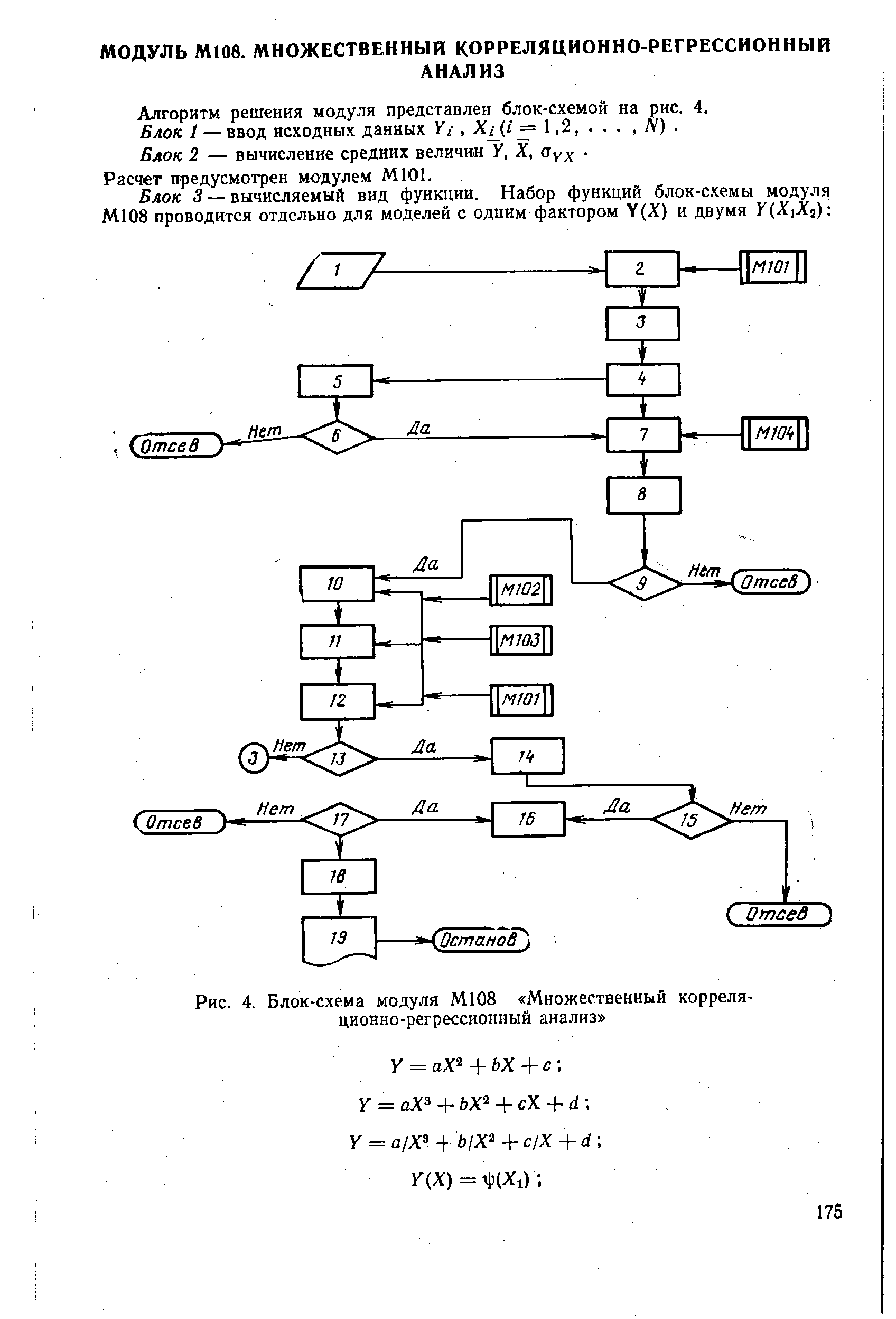 |
Блок 6—построение в каждом классе линейной многофактор-ной корреляционной модели, отражающей зависимость экономических показателей от объективных факторов производства. Корреляционно-регрессивный анализ предусматривается проводить с, помощью модуляМИ Множественный корреляционно-регрессионный анализ . [c.53]
Важный этап в регрессионном анализе — проверка существенности отличия от нуля коэффициента множественной корреляции. Этим проверяется вся построенная модель. Если окажется, что коэффициент множественной корреляции существенно не отличается от нуля, то можно сделать вывод о равенстве нулю всех коэффициентов регрессии и всю модель следует забраковать. Простейший метод проверки существенности (значимости) коэффициента множественной корреляции сводится к построению доверительных интервалов для него и выясне- [c.179]
