Эти функции имеют много общего они равны нулю при х = О, монотонно возрастают, вогнуты. Есть, однако, два важных различия предельная эффективность г/ (30 функции (3.10) при ж- -0 не стремится к бесконечности, а при х-++°° не стремится бесконечности сама функция у (50 она ограничена асимптотой У = Рз Поскольку х = х,/х2, то сильное отличие функции (3.10) от степенной функции при больших и малых значениях х означает, что функция (3.9) отличается от степенной свойствами замещения одного ресурса другим. [c.88]
Проблему наилучшего выбора ограничительных параметров можно сформулировать в виде вопроса где могут произойти в будущем наилучшие и наихудшие сделки (когда мы будем торговать в этой рыночной системе) Хвосты распределения в действительности стремятся к плюс и минус бесконечности, и нам следует финансировать каждый контракт на бесконечно большую сумму (как в последнем примере, где мы раздвигали обе границы). Конечно, если мы собираемся торговать бесконечно долгое время, наше оптимальное f в долларах будет бесконечно большим. Но мы не собираемся торговать в этой рыночной системе вечно. Оптимальное f, при котором мы собираемся торговать в этой рыночной системе, является функцией предполагаемых наилучших и наихудших сделок. Вспомните, если мы бросим монету 100 раз и запишем, какой будет самая длинная полоса решек подряд, а затем бросим монету еще 100 раз, то полоса решек после 200 бросков будет скорее всего больше, чем после 100 бросков. Таким же образом, если проигрыш наихудшего случая за нашу историю 232 сделок равнялся 2,96 сигма (для удобства возьмем 3 сигма), тогда в будущем мы должны ожидать проигрыш больше 3 сигма. Поэтому вместо того, чтобы ограничить наше распределение прошлой историей сделок (-2,96 и +6,94 сигма), мы ограничим его -4 и +6,94 сигма. Нам, вероятно, следует ожидать, что в будущем именно верхняя, а не нижняя граница будет нарушена. Однако это обстоятельство мы не будем принимать в расчет по нескольким причинам. Первая состоит в том, что торговые системы в будущем ухудшают свою результативность по сравнению с работой на исторических данных, даже если они не используют оптимизируемых параметров. Все сводится к принципу, что эффективность механических торговых систем постепенно снижается. Во-вторых, тот факт, что мы платим меньшую цену за [c.138]
| Рис. 56. Усиление степенной зависимости размера s (в условных единицах) типичной самой большой группы как функция силы подражания К. По мере приближения /С к Кс, s отклоняется. Это отклонение воплощает наблюдение, что бесконечно большие группы формируются в критической точке Кс. На практике же, s ограничена размером системы. | 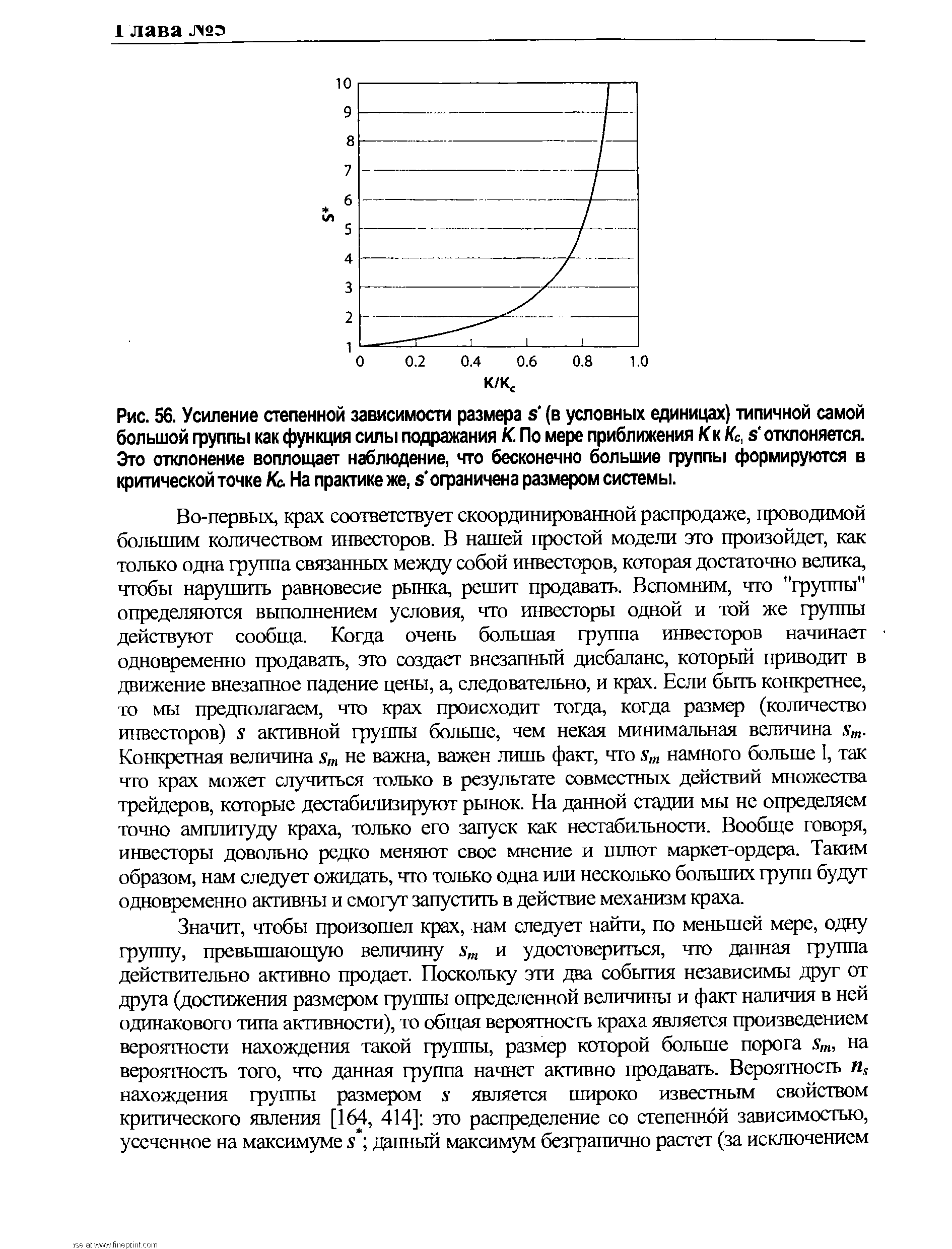 |
Определение. Функция /(ж) называется бесконечно большой величиной при х —> а, если абсолютное значение остается большим любого заранее данного положительного числа М, всякий раз как абсолютное значение разности х — а меньше некоторого положительного числа 6 (зависящего от М). [c.59]
V Пример 1. Целочисленная функция у = 5 п + 1 есть бесконечно большая величина, ибо члены последовательности неограниченно возрастают. А [c.60]
V Пример 3. Целочисленная функция у = tg х есть бесконечно большая величина при х —> —. А [c.60]
Неограниченная функция не обязательно бесконечно большая. Например, функция ж sin ж является неограниченной (ее значения могут быть как угодно большими), но не бесконечно большой при ж — > оо, так как с ростом ж функция все время колеблется, и неравенство ж зтж > М не может выполняться при всех ж, для которых ж > N. [c.61]
Решение. При х — > ос числитель и знаменатель — величины бесконечно большие. Поэтому при непосредственной подстановке символа оо вместо х получаем выражение оо/оо, которое представляет собой неопределенность. Для вычисления предела этой функции нужно и числитель и знаменатель разделить на ж4 (наивысшую степень аргумента в знаменателе) [c.83]
Центральная предельная теорема. Закон больших чисел утверждает, что если объем выборки независимых, одинаково распределенных случайных чисел стремится к бесконечности, ее функция плотности вероятности приближается к нормальному распределению. См. нормальное распределение . [c.291]
Такая формулировка модели позволяет легко получить распределение уровня дефектности в определенный, в том числе и бесконечно большой, момент времени. Как и в других рассмотренных работах, стоимостная функция здесь представляет сумму затрат на контроль, возмещение убытков от [c.136]
В целевую функцию дополнительные переменные вводятся с коэффициентом О , а искусственные - с коэффициентом М (бесконечно большое число). [c.145]
При стохастическом спросе с функцией распределения, определенной для бесконечно больших значений аргумента, при любом конечном запасе существует положительная вероятность недостачи, и принятие цены штрафа d — ос привело бы к бесконечно большим ожидаемым расходам. В подобных случаях часто вводят ограничение по вероятности недостачи. Необходимость экономии на запасах приводит к тому, что вероятность недостачи оказывается в точности равной граничному значению (по крайней мере для непрерывно распределенного спроса). Таким образом, задание вероятности обеспечения полностью определяет решение задачи. Следует, однако, заметить, что обоснование этой цифры невозможно без хотя бы приближенной оценки экономических последствий недостачи, т.е. того же самого штрафа. Сложность этой задачи ни в коей мере не оправдывает субъективного назначения соответствующих вероятностей. Другим возможным подходом является минимизация вероятности или ожидаемого объема дефицита при ограниченных расходах на снабжение. [c.270]
Функция а(х) = - 2 — бесконечно большая при [c.103]
Функция /(Jf)=- — т бесконечно большая при я— 1, [c.103]
Функция f(M), /(М> =О при М=т Мв, является бесконечно большой при N1 -- М тогда и только тогда, [c.103]
Неравенство (2.7) по существу является системой, состоящей из 2" неравенств, соответствующих всем возможным сочетаниям знаков перед слагаемыми dV/dq,. Если q =(qi,...,qn)6 О, то существуют допустимые, не зависящие от времени управления Uj такие, что Ui-9V/5qj=0. Следовательно, dpj/dt=0 для всех i=l,...,n. Такие постоянные управления можно аппроксимировать подвижным управлением вида (2.4)-(2.5) в скользящем режиме, считая, что функция s(t) с бесконечно большой частотой принимает все значения 1<1<л, (бесконечно быстро перемещается между всеми элементами системы), задерживаясь на каждом из них долю времени, пропорциональную величине Uj. [15]. В связи с этим область О, можно назвать "областью застоя" по аналогии с одномерными системами с сухим трением, исследованными в [13]. Таким образом, с помощью построенного алгоритма можно уменьшить до нуля кинетическую энергию системы, но при этом потенциальная энергия будет отлична от нуля. Следует отметить, что в некоторых случаях (например в задачах о демпфировании колебаний) достаточно погасить кинетическую энергию системы, а небольшие постоянные смещения относительно положения равновесия могут быть допустимыми. [c.9]
При достаточно большой эластичности замены (т. е. при достаточно малых значениях р) величина / (0) велика, а для функции Кобба — Дугласа даже бесконечно велика. Поэтому для производственной функции с достаточно большой эластичностью замены условие (4.14) при малых k > 0 выполняться не может, тем более, что параметр г имеет величину порядка нескольких процентов. [c.75]
При анализе предельных случаев производственной функции с постоянной эластичностью замещения (3.7) мы меняли эластичность замещения ресурсов о=1/(1 + р) в интервале от нуля до единицы, что соответствует изменению параметра р от бесконечности до нуля. Возникает естественный вопрос а не может ли эластичность 0 быть больше единицы (меняться от единицы до бесконечности) Такое изменение соответствует изменению параметра р от нуля до минус единицы. Рассмотрим вопрос о том, к какой производственной функции стремится функция с посто- [c.94]
Для выявления циклической составляющей динамики валютного курса статистикой также используется выравнивание по ряду Фурье, поскольку циклические колебания являются разновидностью периодических, как и сезонные. Может применяться и метод скользящей средней. Период скольжения принимают, естественно, другой, соответствующий периоду циклических колебаний. В нашем примере сглаживание целесообразно проводить по 33-месячной скользящей средней (см. рис. 15.3). Период можно определить по графику и с помощью спектрального анализа, представив ряд в виде непрерывной функции, которую можно разложить на сумму бесконечного числа гармонических функций с периодом от 0 до 2л с различной амплитудой. Спектральной плотностью функции называется величина амплитуды гармоники в зависимости о г ее периода. Чем больше амплитуда (спектр) данной гармоники, тем сильнее в использованной функции присутствуют колебания с этим периодом. [c.664]
Поскольку Кипарисов утверждал иное, то можно сказать, что он увидел в Трактате больше, чем там было написано. Точно так же, как Кипарисов подчеркивал контрольные функции бухгалтерский учет уже при Л. Пачоли (а по существу раньше) требует обязательной инвентаризации [Там же, с. 286], это утверждение вполне отвечало пониманию эпохи Большого террора, которая сводила учет в нашей стране к бесконечным инвентаризациям, а самого бухгалтера превращала, если не в сексота, то в официального стукача. [c.338]
Во взаимном фонде средства инвесторов временно объединяются и им открываются счета, отражающие их долю в капитале данного фонда. Фонд время от времени предоставляет клиентам информацию о курсе своих акций и дает им возможность практически в любой момент внести любую дополнительную сумму на свой счет либо забрать деньги обратно. Таким образом, если текущий курс акции фонда составляет 11 долл., а вы вкладываете 1000 долл., то на вашем счете в фонде будет 90,91 акция (1000/11). Это говорит о том, что взаимные фонды, инвестирующие в казначейские векселя, способствуют выполнению четвертой функции финансовой системы, поскольку благодаря им векселя большого достоинства трансформируются практически в бесконечно делимые ценные бумаги. [c.18]
Если для данной величины N ожидаемая выручка больше, чем совокупная цена предложения, т. е. если D больше, чем Z, то предприниматели будут стремиться увеличить занятость сверх N (если даже конкуренция их друг с другом из-за привлечения факторов производства приведет к повышению издержек) до такой величины N, при которой Z стало бы равным D. Таким образом, уровень занятости определяется точкой пересечения функций совокупного спроса и совокупного предложения. Именно в этой точке ожидаемая предпринимателями прибыль будет наибольшей. Величину D в той точке кривой функции совокупного спроса, где она пересекается с функцией совокупного предложения, назовем эффективным спросом. Последующие главы будут посвящены главным образом исследованию различных факторов, от которых зависят обе эти функции ведь в этом и состоит сущность общей теории занятости, выяснение которой является нашей целью. Классическая доктрина, категорически утверждающая, что "предложение само порождает спрос", подразумевает в качестве своей необходимой предпосылки особое отношение между этими двумя функциями. Утверждение "предложение порождает свой собственный спрос" должно означать равенство f(N) i ((N) при любой величине N, т. е. для всех уровней производства и занятости, так что при росте Z=((N), соответствующему росту N,D(= f(N)) должно увеличиться на ту же самую величину, что и Z. Классическая теория предполагает, другими словами, что совокупная цена спроса (или выручка) всегда приспосабливается к совокупной цене предложения. Выходит, что, какова бы ни была величина N, выручка D равна совокупной цене предложения Z, соответствующей той же величине N. Это означает, что объем эффективного спроса вместо того, чтобы соответствовать определенной точке представляет собой бесконечный ряд одинаково приемлемых величин. [c.10]
Ординальные переменные более близки к числовой форме, т.к. числовой ряд также упорядочен. Соответственно, для кодирования таких переменных остается лишь поставить в соответствие номерам категорий такие числовые значения, которые сохраняли бы существующую упорядоченность. Естественно, при этом имеется большая свобода выбора -любая монотонная функция от номера класса порождает свой способ кодирования. Какая же из бесконечного многообразия монотонных функций - наилучшая [c.128]
Если вы хорошо разбираетесь в рынке акций, поздравляем - вы уже чуть-чуть разбираетесь в валютном рынке. Дело в том, что деньги - это те же акции, только акции государств. А государства - это те же компании. Естественно, фирмы бывают разные большие и малые, сильные или слабые. Также и государства - есть третий мир, а есть сверхдержавы. Организационная структура компании чем-то похожа на внутреннее устройство государства. Взять, хотя бы, название должностей и выполняемые функции. Вам не кажется, что Президент государства и Президент компании или Министерство Финансов и финансовый департамент похожи в своих функциях Примеры можно приводить до бесконечности Министерство Торговли и коммерческий департамент, Полиция и внутренняя служба безопасности и так далее, и тому подобное. [c.65]
Теорема (правило Лопиталя-Бернулли). Предел отношения двух бесконечно малых или бесконечно больших функций [c.131]
Два замена льных редела . 82 425 Бесконеч о малые и бесконечно большие функции 83 [c.4]
V Пример 1. Функция у — tgx есть бесконечно большая [ичина при х —) конечный предел [c.61]
Доказательство теорем существования WE, вложения WE с С и обратного вложения, верного для бесконечно большого числа участников, выходит за пределы данного курса 15. Укажем лишь, что важными условиями существования являются выпуклость допустимых множеств и квазивогнутость целевых функций, иначе спрос [c.16]
Еслкръ растет и вместе с ним пропорционально все цены (В) в (А), (С), (D)..., то функция последовательно является возрастающей и убывающей, поскольку она суть сумма последовательно возрастающих и убывающих функций. Тогда действительно товары (А), (С), (D)... становятся все менее дорогими относительно товара (В), и спрос на них проявляет себя последовательно в то же самое время, что и сопровождающее его предложение (В). Но данное предложение не возрастает до бесконечности оно проходит, по меньшей мере, через один максимум, который не может быть больше совокупного имеющегося количества затем оно убывает и снова становится нулевым, если/>ь становится бесконечно большим, т.е. если (А), (С), (D)... бесплатны. [c.111]
В частности, функция одной переменьшй = /( ) является бесконечно большой при х — %, если для любого числа /С> 0 можно указать такое зависящее от К положительное число б, что дивя всех х =хлг удовлетворяющих условию х — в < 6, выполняется неравенство [c.103]
Функция / (х) одной глсер еменной является бесконечно большой при я— >- оо, если дщля любого числа L > 0 можно указать такое зависящее отг L положительное число /С, что для всех х > /С выпо,л и жегся неравенство / (А ) > L. [c.103]
Если А, > 1, то платежная функция в нуле имеет непрерывную и равную нулю производную, каждая ее ветвь в окрестности нуля выпукла, а затем после точки перегиба и до бесконечности - вогнута. Такая функция больше напоминает платежную функцию комбинации двух стрэнглов, одного длинного и одного короткого. При этом страйки обоих стрэнглов расположены симметрично относительно нуля, а страйки длинного стрэнгла ближе к нулю, чем страйки короткого. Эти платежные функции свойственны более расположенным к риску инвесторам. [c.17]
Суть этой проблемы лучше всего объяснить на конкретном примере. Пусть обучающие примеры порождаются некоторой функцией, которую нам и хотелось бы воспроизвести. В теории обучения такую функцию называют учителем. При конечном числе обучающих примеров всегда возможно построить нейросеть с нулевой ошибкой обучения, т.е. ошибкой, определенной на множестве обучающих примеров. Для этого нужно взять сеть с числом весов большим, чем число примеров. Действительно, чтобы воспроизвести каждый пример у нас имеется Р уравнений для W неизвестных. И если число неизвестных меньше числа уравнений, такая система является недоопределенной и допускает бесконечно много решений. В этом-то и состоит основная проблема у нас не хватает информации, чтобы выбрать единственное правильное решение - функцию-учителя. В итоге выбранная случайным образом функция дает плохие предсказания на новых примерах, отсутствовавших в обучающей выборке, хотя последнюю сеть воспроизвела без ошибок. Вместо того, чтобы обобщить известные примеры, сеть запомнила их. Этот эффект и называется переобучением. [c.63]
В качестве последней иллюстрации приведем функцию Вейерштрасса, показанную на Рис. 74, и обладающую действительным значением фрактальной размерности, равным 1,5. Поскольку она проявляет сильную дискретную масштабную инвариантность с предпочтительным масштабным коэффициентом (для последовательных остроконечных структур), равным 2, то она наделена бесконечным числом комплексных фрактальных размерностей, заданных выражением l,5+i2jm/ln2=l,5+i9,06n, где и принимает любое возможное целочисленное значение. По мере того, как целое и растет до все больших и больших значений, соответствующие комплексные размерности описывают все меньшие и меньшие паттерны с дискретной масштабной инвариантностью. [c.208]
